Лекции Физика / Лекция 11.б-1

1

Лекция № 11

Свободные затухающие колебания. Коэффициент затухания. Логарифмический декремент. Энергия гармонического осциллятора. Добротность. Вынужденные колебания, явление резонанса.

Понятие о колебаниях систем со многими степенями свободы.Нормальные колебания (моды). Спектр колебаний, понятие о разложении Фурье.

Уравнение линейного осциллятора:

ω 2 определяется отношением параметров, характеризующих данную колебательную систему:

вслучае колебаний груза массы m , подвешенного на пружине жесткостью k :

ω2 = km ;

вслучае математического маятника:

ω 2 = g l ,

где l - длина маятника, g - ускорение свободного падения;

в случае физического маятника:

m - масса маятника; J - момент инерции маятника относительно оси качания.

Непосредственной подстановкой можно убедиться, что функции sin ωt и cosωt являются частными решениями уравнения (11.1). Общее решение является линейной комбинацией частных решений и представляет собой гармоническую функцию:

ωt + ϕ - фаза колебаний, ω - круговая или циклическая частота,

2

T= 2π ω - период колебаний,

ν= 1T = ω2π - линейная частота.

Единица измерения частоты – Гц = с-1 (1 Гц º 1 колебание в секунду). Различают собственные колебания, затухающие колебания и вынужден-

ные колебания.

Собственными колебаниями называются колебания системы под действием лишь внутренних консервативных сил без внешних воздействий.

Закон сохранения механической энергии для гармонического осциллято-

ра:

Преобразование механической энергии при гармонических колебаниях:

положений.

Смещение, скорость и ускорение при гармонических колебаниях

x(t ) = Acos(ωt + ϕ );

υ(t ) = x&(t ) = -Aω sin(ω t + ϕ );

a(t ) =υ&(t ) = &x&(t ) = -Aω cos(ω t + ϕ ) = -ω 2 x(t );

amax = ω 2 xmax = ω 2 A.

На рис.1 сопоставлены графики для смещения, скорости и ускорения.

Пример.

Пусть механическая система совершает колебания с амплитудой 100 мкм = 10-4 м и круговой частотой 10 кГц. Максимальное значение колебательного ускорения при этом равно (10-4 м)×(104 с-1)2 = 104 м/с2.

3

При массе колеблющегося тела 1 кг мгновенные значения вибрационных нагрузок в системе могут достигать 10 кН!!!

Рис.1

Для определения неизвестных значений амплитуды и фазы гармонических колебаний с известной частотой необходимо знать положение и скорость колеблющегося тела (материальной точки) в некоторый момент времени.

Пусть x(t) = Acos(ω t + ϕ ), тогда υ(t ) = − Asin(ω t + ϕ ). Например, при t = 0 x(t) = Acos(ω t + ϕ ), υ(0) = − Asinϕ , тогда

A = x2 (0) + (υ(0)ω )2 ; ϕ = −arctg(υ(0) x(0)ω ).

Затухающие колебания

При наличии в системе трения (например, при движении колеблющейся материальной точки в вязкой среде) возникает внешняя диссипативная сила трения, приводящая к постепенному убыванию механической энергии системы вследствие ее преобразования во внутреннюю. Система совершает затухаю-

щие колебания.

Уравнение осциллятора в данном случае имеет вид:

4

m&x& = −kx − bx& .

Член bx& описывает силу вязкого трения, пропорциональную скорости движения колеблющегося тела. Разделив обе части на массу колеблющегося тела, получим:

где ω0 = km - частота собственных колебаний осциллятора в отсутствие тре-

ния, b - коэффициент вязкого трения с размерностью [b]= кг/с, γ = b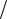2m - декремент (коэффициент) затухания с размерностью [γ ]= 1/с.

Пример колебательной системы с затуханием

Рис.2

В случае малого трения в системе γ < ω0 решение уравнения (11.4) мо-

жет быть представлено в виде:

x(t ) = Aexp(− γt )cos Ωt ,

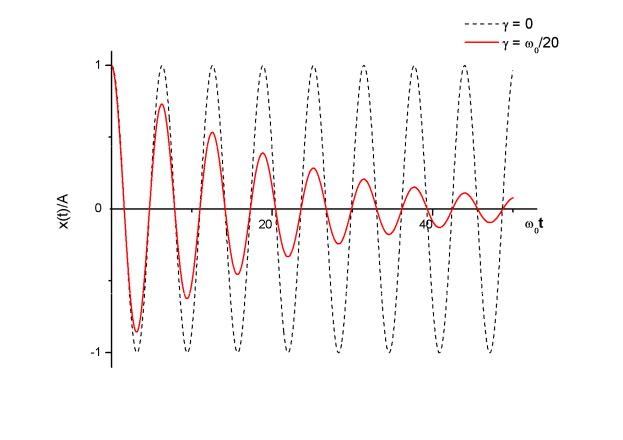
где Ω = 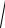ω02 − γ 2 .

Таким образом, ненулевое значение декремента затухания приводит к экспоненциальному спаду значений максимальных отклонений x(t ) от положения равновесия по отношению к исходному значению с течением времени и уменьшению частоты колебаний (рис.3).

5

Рис.3

В случае большого трения в системе γ >> ω0 решение уравнения (11.4)

является апериодическим.

Когда вторым слагаемым (упругой силой) в уравнении (11.4) можно пренебречь по сравнению с третьим (силой вязкого сопротивления) ω02 x << 2γ x& , это уравнение можно переписать как:

&x& = υ& ≈ −γ υ ,

откуда υ(t ) ≈ υ0 exp(− γ t ) - колебания отсутствуют и тело, отклоненное от положения равновесия, возвращается туда со скоростью, убывающей по экспоненциальному закону.

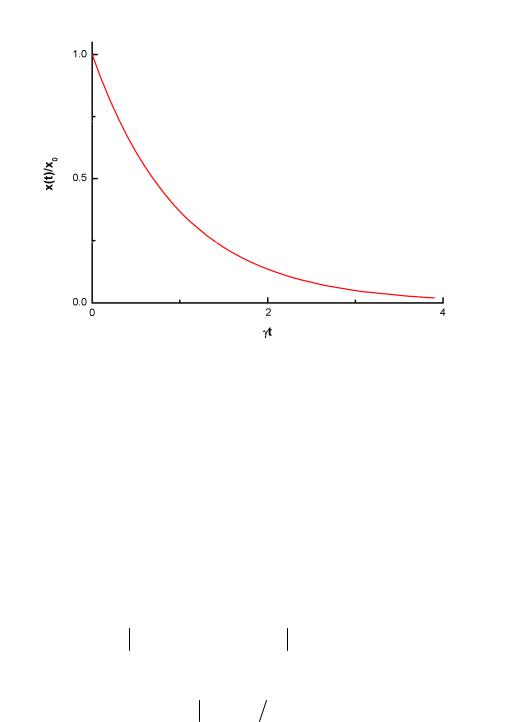
Соответственно, x& ≈ υ0 exp(− γ t ) → x(t ) ≈ x0 exp(− γ t ) (см. рис.4).

6

Рис.4

Для характеристики процесса затухания вводят понятие времени затухания, соответствующего убыванию величины максимального отклонения от положения равновесия в e раз по отношению к исходному значению: τ зат = 1γ .

Декремент затухания недостаточно полно характеризует процесс затухания колебаний, поскольку отсутствует привязка к естественному временному масштабу – периоду колебаний. Поэтому вводится безразмерная величина –

логарифмический декремент затухания θ , характеризующий величину убы-

вания амплитуду колебаний за 1 период.

Можно показать, что отношение амплитуд колебаний в два последовательных момента времени, разделенных периодом колебаний T , равно

xmax (t + T ) xmax (t ) = exp(− γT ).

Логарифмический декремент затухания равен:

Другая интерпретация логарифмического декремента затухания – это величина, обратная числу периодов колебаний, за которое амплитуда колебаний убывает в e раз по отношению к исходному значению: θ = 1 N .

Важной характеристикой также является добротность колебательной системы, равная отношению частоты ее собственных колебаний к удвоенному значению декремента затухания:

7

Вынужденные колебания, явление резонанса.

Дифференциальное уравнение вынужденных колебаний

Все реальные колебания являются затухающими. Чтобы реальные колебания происходили достаточно долго нужно периодически пополнять энергию колебательной системы, действуя на нее внешней периодически изменяющейся силой:

где ωв - частота вынуждающей силы, F – амплитудное значение вынуждающей силы.

Итак, вынужденными колебаниями называют незатухающие колебания, возникающие под действием внешней периодически изменяющейся силы.

где γ = b - коэффициент затухания. 2m

Уравнение (11.11) – неоднородное дифференциальное уравнение второго порядка вынужденных гармонических колебаний.

Решение уравнения вынужденных колебаний

8

Решение уравнения (11.11) равно сумме общего решения однородного уравнения затухающих колебаний:

Слагаемое (11.13) играет существенную роль только в начальной стадии процесса (при установлении колебаний). Графически вынужденные колебания представлены на рис.5. Следовательно, в установившемся режиме вынужденные колебания происходят с частотой ωв и являются гармоническими.

Рис.5

Итак, при приложении внешней силы сначала возникает переходное состояние, при котором физическая система участвует одновременно в двух колебаниях, поэтому решением уравнения (11.11) будет выражение, состоящее из двух слагаемых:

x(t) = x1 (t) + x2 (t) ,

где x1 (t) - решение затухающего колебания,

9

x2 (t) - решение незатухающих периодических колебаний с вынуждающей частотой ωв .

Тогда для установившихся вынужденных колебаний является справедливым уравнение:

где А – амплитуда вынужденных колебаний, ϕ0 - сдвиг фаз между смещением и вынуждающей силой.

Как видим, установившиеся вынужденные колебания являются так же гармоническими. Найдем значение амплитуды А и начальной фазы ϕ0 вынужденных колебаний.

Для этого запишем выражения для скорости и ускорения:

Для упрощения решения можно воспользоваться методом векторных диаграмм:

Рис.6

Из рис.6 видно, что

Из рисунка найдем начальную фазу результирующего колебания ϕ0 (сдвиг фазы между смещением x(t) и вынуждающей силойF (t) ):

Амплитуда и фаза колебаний, определяемые выражениями (11.17) и (11.18), также зависят от ωв .

Механический резонанс

Механическим резонансом называют явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте колебательной системы:

ωв ≈ ω0 .

Т.к амплитуда вынужденных колебаний зависит от частоты вынуждающей силы, построим зависимость А(ωв ) и ϕ0 (ωв ) при различных значениях коэффициента затухания γ (рис.7). Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы называется резонансной характеристикой.

Рис.7. (на рис. γ обозначено через σ )

При ω в = ω 0 подкоренное выражение в (11.17) будет принимать минимальное значение, и выражение примет вид: