Лекции Физика / Лекция 13.б-1

12

Это означает, что газы изменяют свой объем примерно на 1 того объема, ко273

торый каждый из газов занимал при 0 O C , если его температура меняется на

1O C .

Уравнение (13.12) можно записать в другой форме:

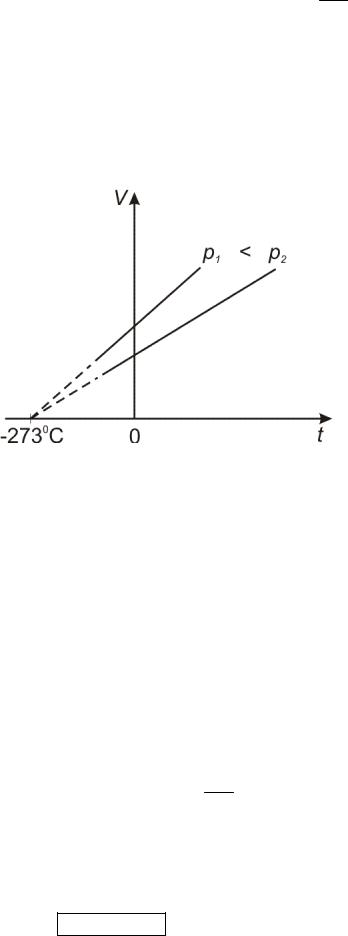
откуда следует, что объем газа определенной массы при p=const меняется линейно при изменении температуры (рис.5).

Рис.6

При увеличении температуры объем газа неограниченно возрастает. Не существует никакого предела для роста температуры. Напротив, низкие температуры имеют предел. Согласно закону Гей-Люссака при понижении температуры объем стремится к нулю. Предельную температуру, при которой объем идеального газа становится равным нулю, принимают за абсолютный нуль температуры. Однако объем реальных газов при абсолютном нуле температуры, согласно современным представлениям термодинамики, обращаться в нуль не может. Имеет ли смысл тогда это предельное значение температуры? Имеет, так как практически можно приблизить свойства реального газа к свойствам идеального. Для этого надо брать всё более разреженный газ, так чтобы его плотность ρ → 0 . У такого газа действительно объем с понижением температуры будет стремиться к предельному, близкому к нулю значению.

В (13.13): приравняем V=0 , учтем α ≈ 1 O C −1 , откуда

Английский ученый Кельвин ввел абсолютную шкалу температур:

T = 273,15 + t , 1O C = 1К .

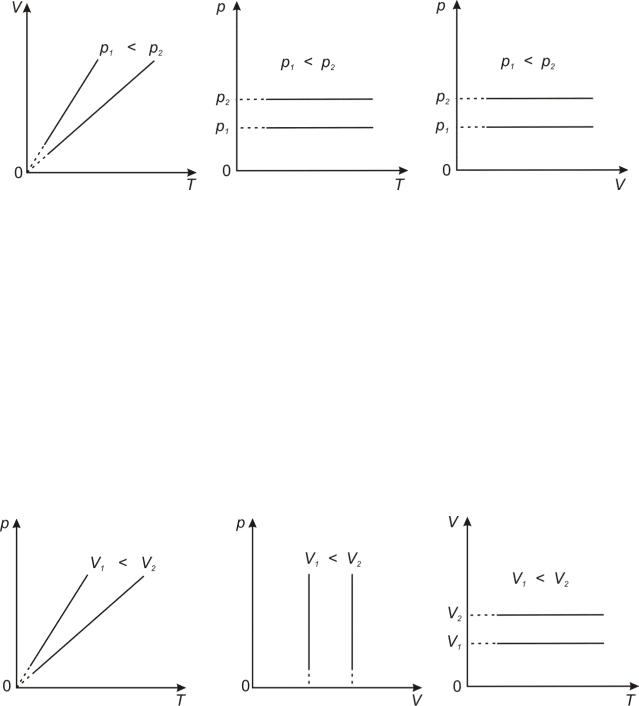
Зависимость объема газа от температуры графически изображается прямой линией – изобарой (рис.7, 8, 9).

Диаграммы (графики) изобарного процесса:

3) Термодинамический процесс, протекающий при постоянном объеме, называется изохорным.

Подчиняется закону Шарля:

Для данной массы газа при постоянном объеме давление газа прямо пропорционально абсолютной температуре:

Зависимость давления газа от температуры графически изображается прямой линией – изохорой (рис.10, 11, 12).

Диаграммы (графики) изохорного процесса:

Теперь определим, чему равна постоянная в уравнении Клапейрона. Мы

{1Па = 1 Н , 1Дж = 1Н × м}

м2 Эту постоянную называют универсальной газовой постоянной:

Пусть теперь ν - произвольное число молей,

ν = m , где m – масса газа, M – его молярная масса.

M

Объем V этого количества вещества при тех же значениях давления и температуры равен:

V =νVM = m VM . M

Умножим обе части уравнения (13.19) на ν = m , тогда получим:

M

pV = m RT - уравнение состояния идеального газа в общем виде, (13.20)

M

называемое уравнением Клапейрона-Менделеева.

В такой форме уравнение состояния было впервые записано великим русским ученым Д.И. Менделеевым.

Уравнение состояния Клапейрона-Менделеева может служить не только для расчета параметров состояния газа, занимающего ограниченный объем ка- кого-либо сосуда. Используя это уравнение, можно достаточно хорошо описать природу наиболее распространенных во Вселенной небесных тел – звезд, типичным представителем которых является Солнце. Солнце, как и многие звезды, представляет собой огромный газовый шар, находящийся в равновесии в собственном поле тяготения.

16

Основное уравнение молекулярно-кинетической теории идеального газа

Вычислим с помощью молекулярно-кинетической теории давление газа. Давление газа объясняется взаимодействием молекул газа со стенками сосуда, которое происходит при соударении с ней.

Давление равно средней силе удара молекул газа о единицу площади стенки со-

суда, в котором находится газ: p = F .

S

Пусть одноатомный идеальный газ находится в прямоугольном сосуде с твердыми стенками. Газ и сосуд имеют одинаковые температуры, т.е. находятся в состоянии теплового равновесия. Будем считать, что число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие ( υR = υR′ ). При этом условии кинетическая энергия молекул в результа-

те столкновения не меняется, т.е. в среднем кинетическая энергия отраженных стенкой молекул будет равна кинетической энергии падающих молекул.

Цель: Вычислим давление газа на стенку сосуда, имеющую площадь S и расположенную перпендикулярно оси x (рис.14).

Рис.14

1 шаг: Определим изменение импульса молекулы при упругом ударе о стенку. Считая, все направления движения молекул равновероятными, можно используя II закон Ньютона выразить силу, действующую со стороны стенки на одну молекулу газа при соударении с этой стенкой.

Изменение проекции импульса молекулы на ось x равно:

импульс, переданный стенке одной молекулой при упругом соударении.

17

По закону Ньютона × D = DR × D = - υ

II : F t p Fст t 2m0 x .

По III закону Ньютона: Fст = -Fмол ,

где, Fст - сила, действующая со стороны стенки на одну молекулу, Fмол - сила, действующая со стороны молекулы на стенку, тогда:

2 шаг: Число молекул, столкнувшихся со стенкой в объеме V со скоростями, проекция υx которых положительна, будет:

Необходимо, однако, учитывать, что реально молекулы движутся к площадке под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется.

3шаг: Импульс, переданный стенке всеми молекулами со скоростями

υx > 0 будет:

4 шаг: Импульс средней силы, действующий на стенку со стороны всех молекул, будет:

Мы знаем определение, что средний квадрат проекции скорости на ось x опре-

деляется:

где суммирование осуществляется по всем проекциям скоростей, как положительным, так и отрицательным. Но положительные значения проекций скоростей встречаются так же часто, как и отрицательные, поэтому:

Учтем, что

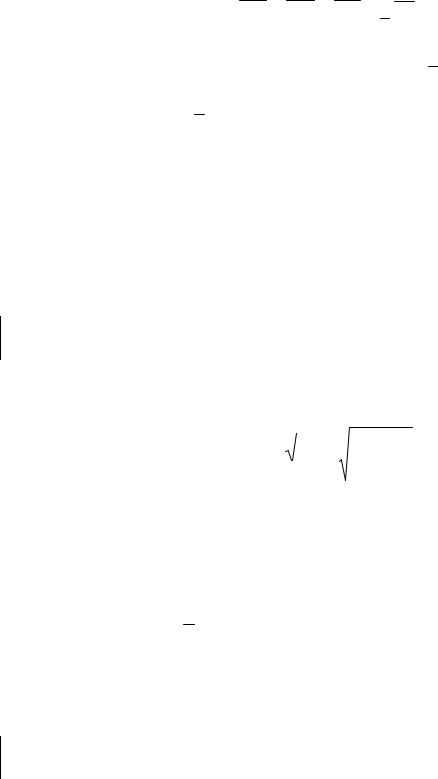
18

υ x 2 = υ y 2 = υ z 2 = 1 υ 2 , 3

то есть средний квадрат проекции скорости равен 1 среднего квадрата самой

3

скорости. Множитель 1 появляется вследствие трехмерности пространства и, 3

значит, существования трех проекций у любого вектора. Тогда в окончательном виде получаем выражение

которое называется основным уравнением молекулярно-кинетической тео-

рии идеальных газов. Точный расчет с учетом движения молекул по всевозможным направлениям дает ту же формулу.

Таким образом, давление идеального газа пропорционально произведению мас- сы молекулы на концентрацию молекул и средний квадрат их скорости.

Здесь ещё раз обращаем своё внимание, что средняя квадратичная скорость определяется:

где N – число молекул в объеме V.

Значимость уравнения (13.29) заключается в том, что оно связывает макропараметр (давление p), характеризующий состояние совокупности огромного числа частиц с микропараметрами (масса и скорость молекулы), характеризующими состояние каждой отдельной молекулы.

Так как средняя кинетическая энергия поступательного движения моле-

Таким образом, давление идеального газа пропорционально средней кинетиче- ской энергии молекул.

Теперь докажем, что температура есть мера средней кинетической энергии молекул. Умножим выражение (13.30) на молярный объем Vм и учтем, что

nVм = N A , тогда

Помним, что уравнение состояния идеального газа для 1 моля имеет вид:

Таким образом, средняя кинетическая энергия хаотического поступательного движения молекул идеального газа пропорциональна его абсолютной темпера- туре и зависит только от неё, т.е. температура есть количественная мера энергии теплового движения молекул.

При одинаковой температуре средние кинетические энергии молекул любого газа одинаковы. При T = 0 К: Eкин = 0 , и поступательное движение молекул газа прекращается, однако анализ различных процессов показывает, что T = 0 К – недостижимая температура.

Подставляя (13.33) в уравнение (13.30), получим следующий вид этого

Таким образом, при одинаковых давлениях и температурах концентрация мо- лекул у всех газов одинаковая.