
Лекции Физика / Лекция 17.б-1
.pdf
1
Лекция № 17
Реальные газы, жидкости и твердые тела.
Критерий различных агрегатных состояний вещества. Уравнение состояния реальных газов. Изотермы Ван-дер-Ваальса и их анализ. Критические параметры. Внутренняя энергия реального газа.
Представления о структуре жидкостей. Твердые тела. Физические типы кристаллов.
Силы и потенциальная энергия межмолекулярного взаимодействия
Простая и удобная модель идеального газа, используемая в МКТ газов, применима в основном к разреженным газам, что соответствует малой плотности вещества. При больших давлениях и низких температурах возникают значительные отклонения от уравнения состояния идеального газа, что указывает на несоответствие модели идеального газа его реальному состоянию.
В1 м3 газа при нормальных условиях содержится 2,68·1025 молекул, занимающих объем примерно 10-4 м3 (радиус молекулы примерно 10-10 м), которым по сравнению с объемом газа можно пренебречь.
При давлении 500 МПа объем молекул уже составит половину всего объема газа. Таким образом, при высоких давлениях и низких температурах указанная модель идеального газа непригодна. Это означает, что уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) следует видоизменить, причем в его новом виде надо учесть отличие реальных молекул газа от модели невзаимодействующих материальных точек, так как реальный газ –
газ, свойства которого зависят от взаимодействия молекул.
ВXX веке, по мере развития представлений о строении атома и квантовой механики, было выяснено, что между молекулами вещества одновременно действуют силы притяжения и силы отталкивания. На рис.1(a) приведена качественная зависимость сил межмолекулярного взаимодействия от расстояния между молекулами, где Fо и Fп соответственно силы отталкивания и притяже-
ния, а F - их результирующая, определяемая выражением:
F = − |
c1 |
+ |
c2 |
, |
|
r 7 |
r13 |
||||
|
|
|
где c1, c2 – коэффициенты, зависящие от химической природы газов.
Силы отталкивания Fо считаются положительными, а силы взаимного притяжения Fп - отрицательными.
На расстоянии r = r0 результирующая сила F = 0 , т.е. силы притяжения и отталкивания уравновешивают друг друга.
При r < r0 преобладают силы отталкивания F > 0 . При r > r0 - силы притяжения F < 0 .
На расстояниях r > 10−9 м межмолекулярные силы взаимодействия практически отсутствуют F → 0 .

2
Рис.1
Элементарная работа δA силы F при увеличении расстояния между молекулами на dr совершается за счет уменьшения взаимной потенциальной энергии молекул, т.е.
δA = Fdr = −dП . |
(17.1) |
На (рис.1(б)) показана зависимость потенциальной энергии двух молекул П от расстояния между молекулами r. Из анализа качественной зависимости потенциальной энергии взаимодействия молекул от расстояния между ними следует, что если молекулы находятся друг от друга на расстоянии r → ∞ , на котором межмолекулярные силы взаимодействия не действуют, то П = 0 .
При постепенном сближении молекул между ними появляются силы притяженияF < 0 , которые совершают положительную работу
δA = Fdr > 0 .
Тогда, согласно (17.1), потенциальная энергия взаимодействия уменьшается,

3
достигая минимума при r = r0 .
При r < r0 с уменьшением r силы отталкивания F > 0 резко возрастают и совершаемая против них работа отрицательна
δA = Fdr < 0 .
Потенциальная энергия начинает тоже резко возрастать и становится положительной.
Из данной потенциальной кривой следует, что система из двух взаимодействующих молекул в состоянии устойчивого равновесия (при r = r0 ) обладает минимальной потенциальной энергией Пmin .
Критерием различных агрегатных состояний вещества является соот-
ношение между величинами Пmin и kT:
Пmin - наименьшая потенциальная энергия взаимодействия молекул – опреде-
ляет работу, которую нужно совершить против сил притяжения для того, чтобы разъединить молекулы, находящиеся в равновесии ( r = r0 ).
kT - определяет удвоенную среднюю энергию, приходящуюся на одну степень свободы хаотического (теплового) движения молекул.
1) Газообразное состояние вещества.
Если Пmin << kT , то вещество находится в газообразном состоянии, так как интенсивное тепловое движение молекул препятствует соединению молекул, сблизившихся до расстояния r0 . То есть вероятность образования агрегатов из молекул достаточна мала.
2) Твердое состояние вещества.
Если Пmin >> kT , то вещество находится в твердом состоянии, так как молекулы, притягиваясь друг к другу, не могут удалиться на значительные расстояния и колеблются около положений равновесия, определяемого расстоянием r0 . То есть тепловой энергии недостаточно, чтобы “ оторвать” молекулы друг от друга.
3) Жидкое состояние вещества.
Если Пmin ≈ kT , то вещество находится в жидком состоянии, так как в результате теплового движения молекулы перемещаются в пространстве, обмениваясь местами, но не расходясь на расстояние, превышающее r0 .
Вывод: любое вещество в зависимости от температуры может находиться в газообразном, жидком или твердом агрегатном состоянии, причем температура перехода из одного агрегатного состояния в другой зависит от значения Пmin для данного вещества.
Например, у инертных газов Пmin мало, а у металлов велико, поэтому при обычных (комнатных) температурах они находятся соответственно в газообразном и твердом состояниях.
Уравнение Ван-дер-Ваальса – это уравнение состояния реальных газов. Для реальных газов необходимо учитывать размеры молекул и их взаи-
модействие друг с другом, поэтому модель идеального газа и уравнение Мен-
4
делеева-Клапейрона pVm = RT (для моля газа), описывающее идеальный газ, для реальных газов непригодны.
Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, Ван-дер-Ваальс вывел уравнение состояния реального газа. В уравнение Менделеева-Клапейрона введены две поправки.
1) Учет собственного объема молекул.
Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не Vm , а
(Vm − b ), |
(17.2) |
где b - объем, занимаемый самими молекулами.
Покажем, что объем b равен учетверенному собственному объему моле-
кул.
Если d - диаметр молекулы, то каждая молекула реального газа имеет
объем V0 = πd 3 . 6
Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние d, меньшее диаметра молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса d, то есть
V |
= |
4 |
πd 3 = |
4 × 6 |
πd 3 = 8V . |
|
|
|
|||||
сфер |
3 |
3 6 |
0 |
|||
Запрещенный объем равен восьми объемам молекулы или учетверенному объему молекулы в пересчете на одну молекулу: b = 4N AV0 .
2) Учет притяжения молекул.
Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением p'.
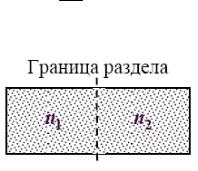
Определим p'. Для этого представим объем газа в виде двух частей
(рис.2) с концентрациями n1 = n2 ~ 1 .
Vm
Рис.2
Силы притяжения первой и второй частей пропорциональны концентрации молекул в поверхностных слоях у границы раздела, поэтому по вычислениям Ван-

5
дер-Ваальса, внутреннее давление обратно пропорционально квадрату молярного объема, занимаемого газом:
p'= |
a |
, |
(17.3) |
|
|||
V 2 |
|
|
|
|
m |
|
|
где a - параметр, зависящий только от природы газа, называется постоянная Ван-дер-Ваальса (имеет табличное значение для конкретного газа); Vm - молярный объем.
Давление, производимое на стенки реальным газом, меньше, чем в случае идеального газа, не величину p'.
Вводя эти поправки, получим уравнение Ван-дер-Ваальса для 1 моля газа
(уравнение состояния реальных газов):
|
a |
|
|
|
|
|
p + |
(V - b) = RT |
. |
(17.4) |
|||
|
||||||
|
2 |
m |
|
|
||
|
Vm |
|
|
|
||
Для произвольного количества вещества ν газа с учетом того, что
ν = m , Vm = V , M ν
уравнение Ван-дер-Ваальса примет вид:
|
|
ν 2a |
V |
|
|
|||||||||
|
p + |
|
|
|
|
|
|
|
|
− b = RT |
|
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
V 2 |
|
ν |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν |
2 |
a |
|
|
|
|
|
|||
|
p + |
|
|
(V |
-ν × b) =ν × RT |
, |
(17.5) |
|||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
V |
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где поправки a и b - постоянные для каждого газа величины, определяемые опытным путем. Записываются уравнения Ван-дер-Ваальса для двух известных из опыта состояний газа и решаются относительно a и b.
При выводе уравнения Ван-дер-Ваальса сделан целый ряд упрощений, поэтому оно также весьма приближенное, хотя и лучше (особенно для несильно сжатых газов) согласуется с опытом, чем уравнение состояния идеального газа.
Уравнение Ван-дер-Ваальса не единственное уравнение, описывающее реальные газы. Существуют и другие уравнения, некоторые из них даже точнее описывают реальные газы, но не рассматриваются из-за их сложности.
Изотермы реальных газов
Если в уравнении Ван-дер-Ваальса для одного моля реального газа
p +
a |
|
|
|
|
(V |
- b) = RT |
|||
2 |
||||
|
m |
|
||
Vm |
|
|
|
|
раскрыть скобки и привести уравнение к общему знаменателю, то получится уравнение третьей степени относительно Vm при заданных p и Т:
6
pV 3 |
− (pb + RT )V 2 |
+ aV − ab = 0 . |
(17.6) |
m |
m |
m |
|
Данное уравнение для конкретного давления р1 может иметь три вещественных корня Vm1 , Vm2 , Vm3 , либо один вещественный и два мнимых, причем физиче-
ский смысл имеют лишь вещественные положительные корни. Поэтому перво-
му случаю соответствуют изотермы при низких температурах (три значения объема газа отвечают одному значению давления), второму случаю – изотермы при высоких температурах.
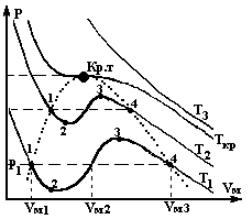
Зависимости р от Vm , построенные из данного уравнения при различных температурах, - это изотермы Ван-дер-Ваальса (рис.3).
Рис.3. Изотермы Ван-дер-Ваальса.
Видим, что пока температура не достигнет некоторого критического значения Ткр, в пространстве (р,V) имеется область, где каждому значению давления соответствуют три точки изотермы с тремя различными Vm – три корня уравнения Ван-дер-Ваальса. По мере повышения температуры эти три точки сближаются и при Т=Ткр сливаются в одну точку, которая является точкой перегиба критической изотермы. При Т > Ткр изотермы Ван-дер-Ваальса близки к изотермам идеального газа.
Английский физик Т.Эндрюс в 1866г. экспериментально исследовал зависимость молярного объема углекислого газа СО2 от давления при изотермическом сжатии (рис.4). Было замечено, что при температурах, меньшей некоторой критической (Tкр = 340 К) на изотермах имеется горизонтальный участок
В-С, на котором постоянно давление, а молярный объем возрастает от VВ до VС , причем, чем ниже Т, тем больше разность (VС – VВ). При приближении к Tкр эта
разность стремится к нулю. Кривую, снятую при Tкр называют критической
изотермой. На ней точки В и С сливаются в одну точку К, называемую
критической точкой.

7
Рис.4. Изотермы углекислого газа СО2.
Любую “ докритическую” изотерму можно разбить на три характерных участка: АВ, ВС и СD. На участках АВ и СD при уменьшении объема давление возрастает, а на участке СВ – не меняется. Это своеобразие докритических изотерм связано с тем, что они охватывают различные агрегатные состояния СО2 : на участке АВ состояние системы характеризуется большой плотностью и малой сжимаемостью, что соответствует жидкости. На участке СD состояние системы характеризуется низкой плотностью и легкой сжимаемостью, что соответствует газообразному состоянию, а на участке ВС углекислота одновременно находится в 2-х агрегатных состояниях – жидком и газообразном. Если мы будем уменьшать объем газа, сжимая его, т.е. двигаться в направлении от С к В, то точка С будет соответствовать началу конденсации СО2, а точка В – ее концу. Если же двигаться наоборот, от В к С (изотермическое расширение), то точка В будет соответствовать началу кипения, а точка С – его окончанию. Другими словами, точка В соответствует состоянию кипящей жидкости, а
точка С – сухого насыщенного пара. В любой другой точке на участке ВС СО2 представляет собой смесь кипящей жидкости и сухого насыщенного пара. Та-
кую смесь называют влажным паром. Он представляет собой двухфазную сис-
тему.
С ростом Т прямолинейный участок сокращается по длине, точка В смещается вправо, С – влево. Объясняется это тем, что молярный объем жидкости, находящейся в равновесии с насыщенным паром, увеличивается с ростом температуры, так как при этом в жидкости ослабевают межмолекулярные силы сцепления. Молярный же объем насыщенного пара, напротив, уменьшается. При T = Tкр , p = pкр , Vm = Vmкр точки В и С сливаются в одну и газ целиком переходит в жидкость, минуя двухфазное состояние.
Из сопоставления изотермы Ван-дер-Ваальса с реальной изотермой Энд-
рюса вытекает, что они примерно совпадают на участках, отвечающих однофазным состояниям вещества, но ведут себя совершенно различным образом в области расслоения на две фазы. Вместо S-образного завитка на изотерме Ван-
8
дер-Ваальса реальная изотерма имеет в этой области прямолинейный горизонтальный участок.
Оказывается, что при некоторых условиях состояния, соответствующие участкам 1-2 и 3-4 (рис.3) могут осуществиться. Правда, они не вполне устойчивы. Такие состояния называются метастабильными. Вещество в состояниях 1-2 называется перегретой жидкостью, вещество в состояниях 3-4 называется
пересыщенным (переохлажденным) паром. Участок кривой 2-3 практически воспроизведен быть не может, так как это состояние противоречит условию стабильности системы.
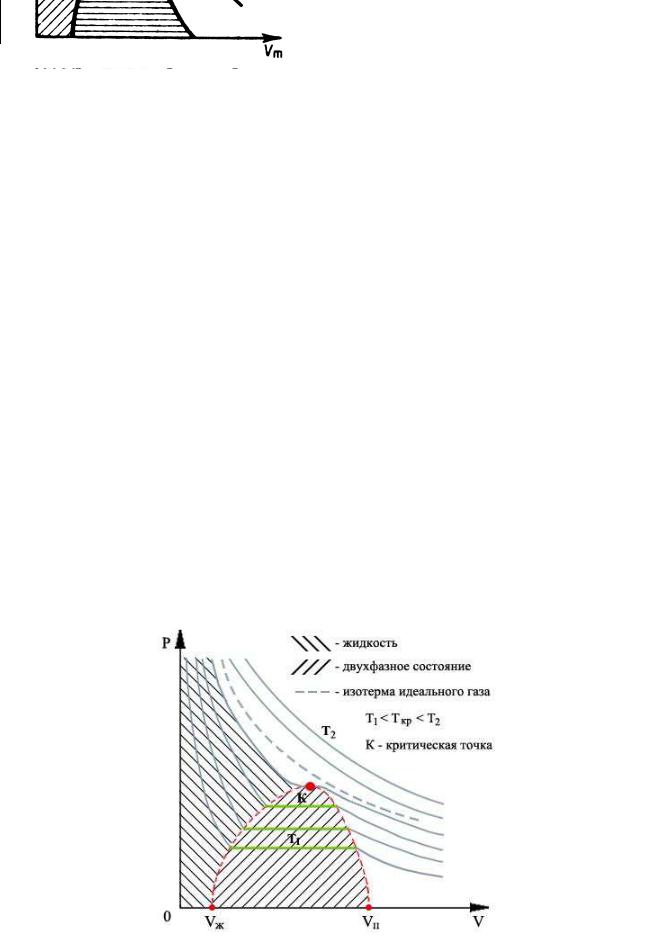
Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая (см. рис.5, а также рис.5*), ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму под изотермой на три области: под колоколообразной кривой располагается
область двухфазных состояний (жид-
кость и насыщенный пар), слева от нее находится область жидкого состояния, а справа - область пара. Пар отличается от всех остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращен в жидкость ни при каком давлении.
Рис.5
Рис.5*

9
Таким образом, важным следствием уравнения состояния неидеально газа является возможность фазового перехода вещества из одного состояния в другое. Кривые на диаграммах p,V или V,T, отделяющие области существования разных фаз, — это кривые фазового равновесия. Они показывают, при каких значениях параметров вещество может существовать в одном из состояний — твердом, жидком либо газообразном.
На рис.6 в координатах p, Т изображена, например, фазовая диаграмма для двуокиси углерода, на которой показаны области существования всех трех возможных фаз.
Рис.6
Критическая температура для CO2 равна 216,6 К, что составляет - 56,6O С . При обычных температурах и давлениях жидкая фаза не реализуется. В твердой фазе CO2 представляет собой сухой лед. Он потому и называется сухой, что имеет низкую температуру, но не плавится, а сразу превращается в газовую фазу.
Внутренняя энергия реального газа
Внутренняя энергия реального газа равна сумме кинетической энергии хаотического теплового движения молекул (определяет внутреннюю энергию идеального газа, равную СV T ) и их взаимной потенциальной энергии:
U = Eкин + П . |
(14.*) |
Потенциальная энергия реального газа обусловлена только силами притяжения между молекулами. Наличие сил притяжения приводит к возникновению внутреннего давления на газ:
p'= a . Vm2
Работа, которая затрачивается для преодоления сил притяжения, действующих между молекулами газа, идет на увеличение потенциальной энергии системы:
δA = p'dVm = dП ,

10
то есть |
|
|
|
|
|
||
dП = |
|
a |
|
dV |
m |
, |
(14.2) |
|
|
||||||
V 2 |
|
|
|
|
|||
|
|
m |
|
|
|
|
|
откуда |
|
|
|
|
|
||
П = − |
a |
|
, |
|
|
(14.3) |
|
|
|
|
|
||||
|
Vm |
|
|
|
|
|
|
здесь постоянная интегрирования принята равной нулю. Знак “ минус” означает, что молекулярные силы, создающие внутреннее давление p', являются силами
притяжения.
Учитывая оба слагаемых в (14.*), получим,
ля реального газа:
Um = СV T − a ,
Vm
где СV - молярная теплоемкость при V = const , Т – термодинамическая температура, а – постоянная Ван-дер-Ваальса,
Vm - молярный объем.
что внутренняя энергия 1 мо-
(14.4)
Из выражения (14.4) следует, что внутренняя энергия реального газа растет с повышением температуры и увеличением объема.
Представления о структуре жидкостей, ближнем порядке
Жидкость является агрегатным состоянием вещества, промежуточным между газообразным и твердым. Поэтому она обладает свойствами как газообразных, так и твердых веществ.
Жидкости, во-первых, подобно твердым телам, обладают определенным объемом, а во-вторых, подобно газам, принимают форму сосуда, в котором они находятся.
Молекулы газа практически не связаны между собой силами межмолекулярного взаимодействия. Средняя энергия теплового движения молекул газа гораздо больше средней потенциальной энергии, обусловленной силами притяжения между ними, поэтому молекулы газа разлетаются в разные стороны, и газ занимает предоставленный ему объем.
Втвердых и жидких телах силы притяжения между молекулами уже существенны и удерживают молекулы на определенном расстоянии друг от друга.
Вэтом случае средняя энергия хаотического (теплового) движения молекул меньше средней потенциальной энергии, обусловленной силами межмолекулярного взаимодействия, и ее недостаточно для преодоления сил притяжения между молекулами, поэтому твердые тела и жидкости имеют определенный объем.
Врасположении частиц жидкости наблюдается так называемый ближний порядок. Это означает, что по отношению к любой частице расположение ближайших к ней соседей является упорядоченным. Однако по мере удаления от
