9Уравнения Лагранжа в случае потенциальных сил. Циклические координаты и циклические интегралы

В случае потенциальных сил обобщенные силы определяются через потенциальную энергию системы соотношениями:

.

Тогда уравнения Лагранжа

.

перепишутся в виде:

.

 

Введем функцию Лагранжа соотношением: . 

Учитывая, что потенциальная энергия есть функция только обобщенных координат:

,

имеем:

 .

 

Если в функцию Лагранжа не входят явно обобщенных координат , то возможно частичное интегрирование дифференциальных уравнений движения механической системы. Соответствующие обобщенные координаты называютсяциклическими. Для них:

.

 

Тогда 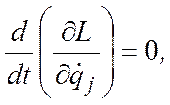 откуда находим общих, так называемыхциклических интегралов системы дифференциальных уравнений движения механической системы: 

10 Положение равновесия механической системы и ее устойчивость. Теорема Лагранжа-Дирихле. 2 теоремы Ляпунова о неустойчивости.

Условие равновесия механической системы с голономными, стационарными и идеальными связями в обобщенных координатах имеет вид: 

,

а в случае действия только потенциальных сил ( для консервативных систем)

₍₁₎

Эта система уравнений относительно обобщенных координат позволяет найти все положения равновесия консервативной механической системы. Из них только устойчивые реализуются на практике и представляют интерес.

 Положение равновесия механической системы, имеющей  степеней свободы   устойчиво (по Ляпунову), если для любых  существуют , , такие, что при начальных возмущениях  и ,  в дальнейшем движении механической системы для каждой обобщенной координаты выполняется неравенство  ,.   В противном случае положение равновесия называется неустойчивым.  

Достаточный критерий устойчивости дает

Теорема Лагранжа-Дирихле.

Если в положении равновесия консервативной механической системы с идеальными  и стационарными связями потенциальная энергия имеет локальный минимум, то это положение равновесия устойчиво.

 Для механических систем с одной степенью свободы условие минимума потенциальной энергии в положении равновесия  определяется на основе соответствующих теорем математического анализа о необходимых и достаточных условиях существования экстремума функции одной переменной:

 ,   

Для исследования устойчивости положения равновесия механической системы с несколькими степенями свободы разложим потенциальную энергию в ряд в окрестности положения равновесия. С точностью до членов более высокого порядка малости, потенциальная энергия механической системы в окрестности положения равновесия может быть представлена квадратичной формой. Так как потенциальная энергия в положении равновесия равна нулю, и в этом положении она имеет минимум, то вблизи положения равновесия П > 0, т . е . соответствующая квадратичная форма определенно

положительна. Математическое условие положительной определенности любой квадратичной формы дается теоремой Сильвестра: Для того чтобы квадратичная форма была определенно положительной, необходимо и достаточно, чтобы все главные миноры матрицы квадратичной формы были положительными.

В некоторых случаях проще установить неустойчивость равновесия на основании теорем Ляпунова.

теорема 1. Равновесие консервативной системы неустойчиво, если потенциальная энергия системы в положении равновесия не имеет минимума и отсутствие минимума определяется слагаемыми второго порядка малости в разложении потенциальной энергии в ряд по степеням обобщенных координат.

теорема 2. Равновесие консервативной системы неустойчиво, если потенциальная энергия системы в положении равновесия имеет максимум и наличие максимума определяется членами наименьшего порядка малости в разложении потенциальной энергии в ряд по степеням обобщенных координат.