16Теорема о движении центра масс смт

Считая, что массы МТ постоянны, преобразуем формулу, определяющую количество движения СМТ, следующим образом:

. (1)

На основании определения центра масс 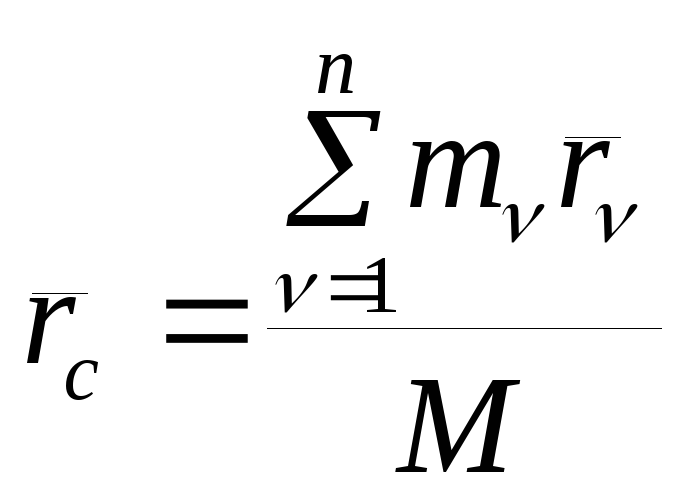, поэтому:

(2)

Подставляя соотношение (2) в (2), получим:

Таким образом, количество движения СМТ равно количеству движения, которое имел бы центр масс СМТ, если бы в нем была сосредоточена вся масса СМТ

. (3)

Подставляя (3) в теорему об изменении количества движения СМТ

получим теорему о движении центра масс СМТ в векторной форме:

(4)

Теорема: Центр масс СМТ движется как МТ, в которой сосредоточена вся масса СМТ и к которой приложены все внешние силы, действующие на СМТ.

Проектируя второе соотношение формул (4) на оси декартовой системы координат, получим дифференциальные уравнения движения центра масс СМТ в проекциях на оси декартовой системы координат:

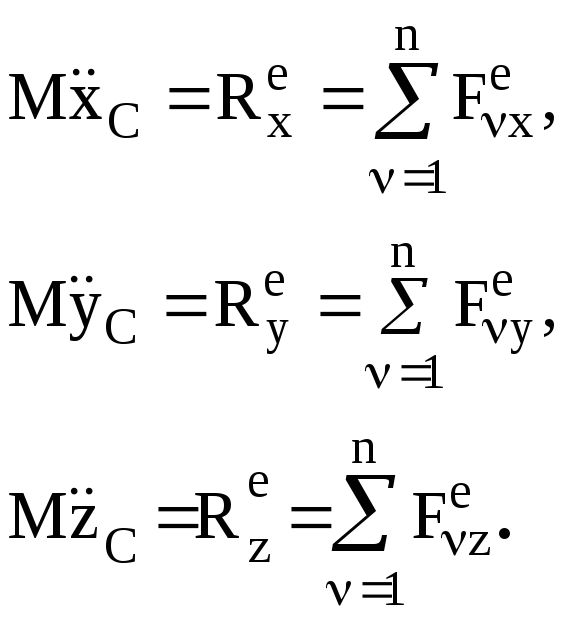(5)

Из теоремы о движении центра масс СМТ можно получить два следствия, аналогичные закону сохранения количества движения СМТ.

Следствия:

• Если 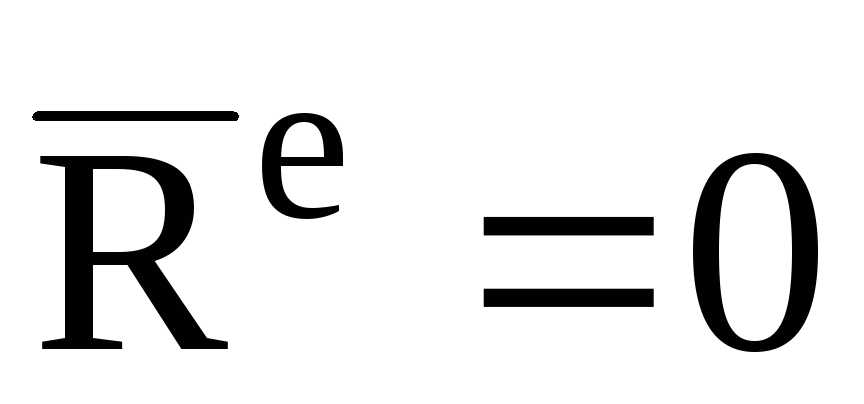, то из первого соотношения формул (4) следует, что

.

Если главный вектор внешних сил, действующих на СМТ, равен нулю, то СМТ движется так, что скорость центра масс СМТ постоянна по величине и направлению и равна скорости центра масс в начальный момент времени.

Если (для определенности выбрана ось х), то из первого соотношения уравнений (5) следует, что

.

Если проекция главного вектора внешних сил СМТ на какую-либо ось равна нулю, то СМТ движется так, что проекция скорости центра масс СМТ на эту ось является постоянной величиной и равна проекции скорости центра масс на эту ось в начальный момент времени.

17Теорема об изменении кинетического момента смт

Запишем теорему об изменении момента количества движения МТ для -й точки СМТ, учтя, что на нее действуют – равнодействующая всех внешних сил и – равнодействующая всех внутренних сил:

. (=1,2,...,n)

Просуммировав эти выражения и учитывая, что сумма производных равна производной от суммы, получим:

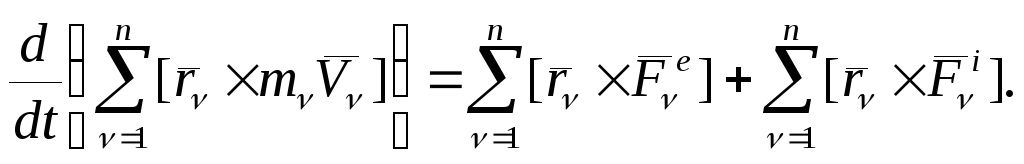(1)

Используя формулу для главного момента системы сил и учтя свойство внутренних сил, имеем:

,, (2)

где - главный момент всех внешних сил, а- главный момент всех внутренних сил относительно какого-либо центра.

Введем понятие кинетического момента СМТ относительно какого-либо центра О.

Определение: Кинетическим моментом или моментом количества движения СМТ называется геометрическая сумма моментов количества движения МТ, входящих в СМТ, относительно того же центра:

. (3)

Подставив (2) и (3) в (1), получим теорему об изменении кинетического момента СМТ в следующем виде:

. (4)

Теорема: Производная по времени от кинетического момента СМТ относительно какого-либо центра равна главному моменту всех внешних сил, действующих на СМТ, относительно того же центра.

Спроектировав соотношения (4) на оси декартовой системы координат с началом в центре О и учтя связь между моментами силы относительно точки и оси, получим:

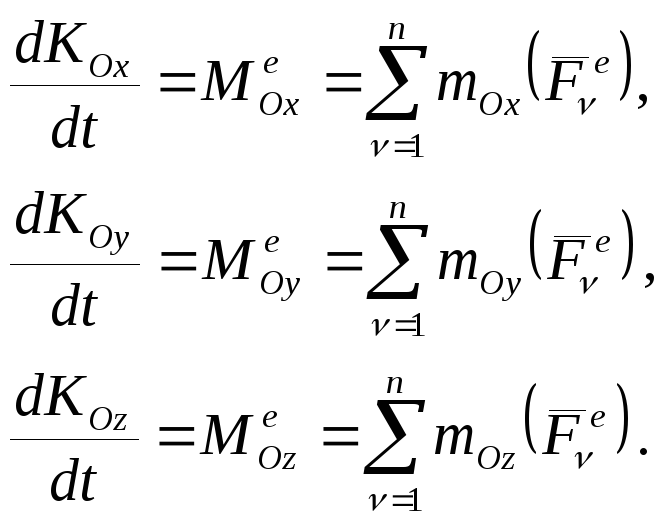(5)

Отсюда следует, что производная по времени от проекции кинетического момента СМТ на какую-либо ось равна проекции главного момента всех внешних сил, действующих на СМТ, на эту ось или сумме моментов всех внешних сил, действующих на СМТ, относительно этой оси.

Следствия:

• Если 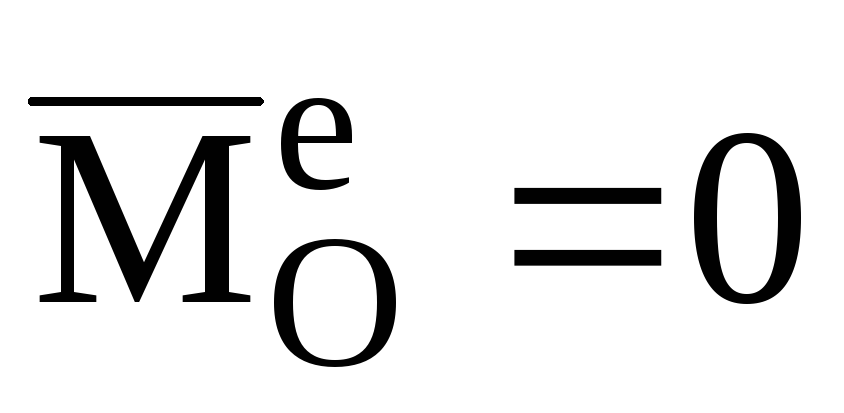, то из соотношения (4) следует, что

. (6)

Если главный момент внешних сил, действующих на СМТ, относительно какого-либо центра равен нулю, то кинетический момент СМТ относительно того же центра постоянен по величине и направлению и равен кинетическому моменту СМТ относительно того же центра в начальный момент времени:

Если (для определенности выбрана ось х), то из первого соотношения (4.25) следует, что

.

Если проекция главного момента всех внешних сил, действующих на СМТ, на какую-либо ось (сумма моментов всех внешних сил относительно какой-либо оси) равна нулю, то проекция кинетического момента на эту ось является постоянной величиной и равняется проекции кинетического момента на эту ось в начальный момент времени