27Обобщенные координаты, обобщенные силы. Условия равновесия смт в обобщенных координатах

Независимые параметры, достаточные для однозначного определения положения рассматриваемой механической системы, называются ее обобщенными координатами .

Число независимых параметров , однозначно определяющих положение системы в пространстве, называется числом ее степеней свободы.

Для каждой из МТ, входящей в СМТ, радиус-вектор можно выразить через обобщенные координаты, которые являются функциями времени:

=1,2,…,n (1)

Найдем вариацию радиуса-вектора -й точки системы:

. (2)

Подставляя эти значения в соотношение (1.11) и изменяя порядок суммирования, получим:

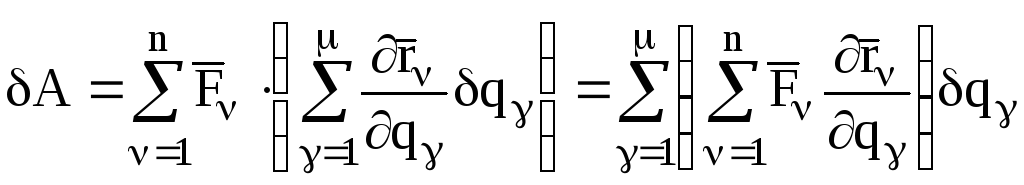. (3)

Введем обозначения:

. (4)

Тогда выражение для работы сил на виртуальных перемещениях через обобщенные координаты примет вид:

. (5)

Множители Q₁,Q₂,…,Q_, стоящие в формуле (6) перед вариациями обобщенных координат, называются обобщенными силами, отнесенными к соответствующим обобщенным координатам.

Возможны три способа нахождения обобщенных сил:

• по формуле (4).

• по формуле (5), определив обобщенные силы как коэффициенты при вариациях обобщенных координат в выражении суммы элементарных работ всех сил на виртуальных перемещениях. Учитывая, что вариации обобщенных координат независимы и могут принимать произвольные значения, дадим системе такое виртуальное перемещение, при котором вариации всех обобщенных координат, кроме одной, будут равны нулю, например, 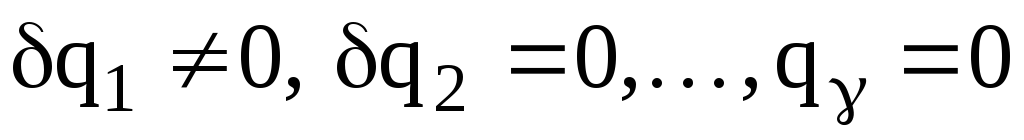, (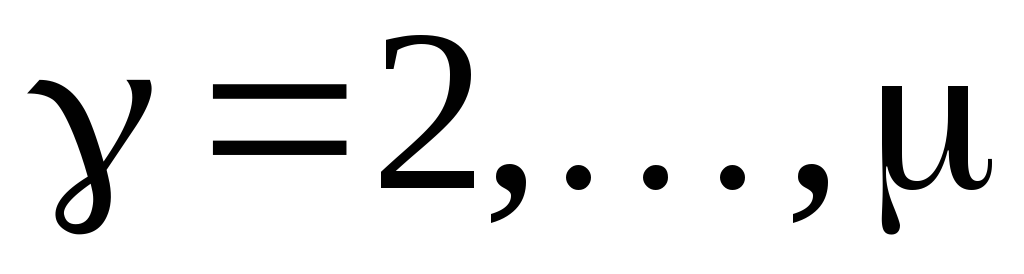). Тогда из соотношения (5) находим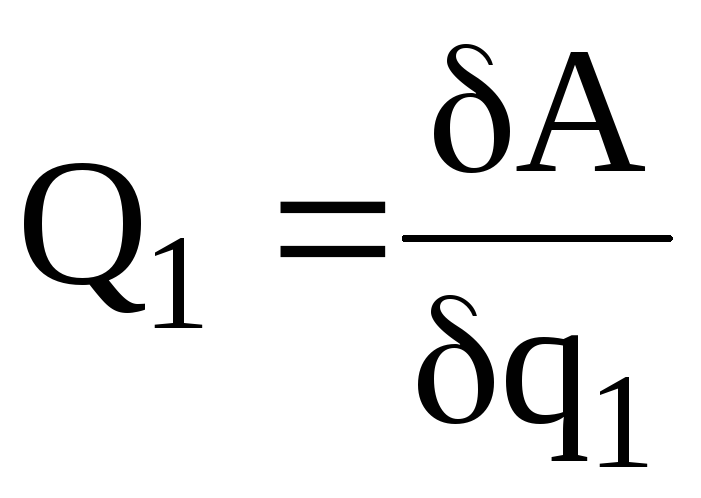, и так далее для всех обобщенных сил.

• когда система находится в потенциальном силовом поле для проекций силы, приложенной к -й точке, можно записать:

,

где U(x,y,z) – силовая функция, а – потенциальная энергия. Подставляя эти значения в соотношения (5) и учитывая, что П зависит от обобщенных координат сложным образом, имеем:

.

Условия равновесия механической системы в обобщенных координатах: Для равновесия СМТ, на которую наложены стационарные, удерживающие и идеальные связи, необходимо и достаточно, чтобы все обобщенные силы равнялись нулю:

.

Запишем выражение принципа виртуальных перемещений с учетом соотношения (5):

. (6)

Доказательство: Так как вариации обобщенных координат независимы и произвольны, то можно сообщить системе такое виртуальное перемещение, при котором вариации всех обобщенных координат, кроме одной, например первой, равны нулю

(7)

Подставляя (7) в (6) получим и так далее для всех обобщенных сил.

28. Уравнения Лагранжа второго рода (Уравнения движения смт в обобщенных координатах)

Используем следующую форму общего уравнения динамики:

. (1)

Пусть на механическую систему, имеющую  степеней свободы, нало­жены голономные, удерживающие и идеальные связи. Введем в рассмотрение  обобщенных координат q_ (=1,…,) и выразим через них радиус-вектор -й точки:

, . (2)

Варьируя это соотношение, получим:

, . (3)

Подставляя соотношение (3) в соотношение (1) и изменяя порядок суммирования, имеем:

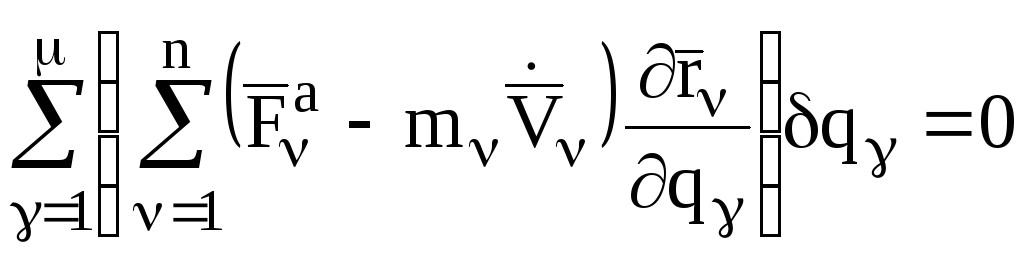. (4)

Так как все независимы и произволь­ны, то равенство (4) может выполняться только тогда, когда каждый из коэффициентов при равен нулю, поэтому нахо­дим:

. (5)

Эту систему  уравнений запишем в виде:

. (6)

Правая часть соотношения (6) представляет собой обобщенную силу соответствующую обобщенной координате :

. (7)

Преобразуем выражение, входящее в левую часть соотношения (6) следующим образом:

(8)

Учитывая, что радиус-вектор -й МТ зависит от времени t сложным образом, получим из(2)следующее выражение для ее скорости:

, (9)

где – называется обобщенной скоростью ( = 1, 2,…, ).

Так как множители ( = 1, 2,…, ) зависят только от обобщенных координат и времени t (и не зависят от обобщенных скоростей), то дифференцируя правую и левую часть соотношения (9) по обобщенной скорости , приходим к соотношению:

. (10)

Найдем частную производную скорости по обобщенной координате, учитывая, что обобщенные координаты входят в правую часть равенства (9) через коэффициенты при обобщенных скоростях:

. (11)

Частная производная зависит от времениt явно и через обобщенные координаты , (). Вычисляя полную производную по времени от частной производной находим:

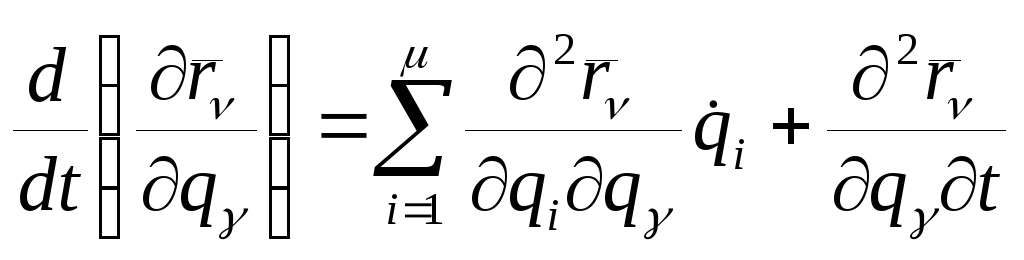. (12)

Сравнивая правые части выражений (11) и (12), замечаем, что

. (13)

Возвращаясь к формуле (8) и подставляя в нее тождества (19) и (13), получаем:

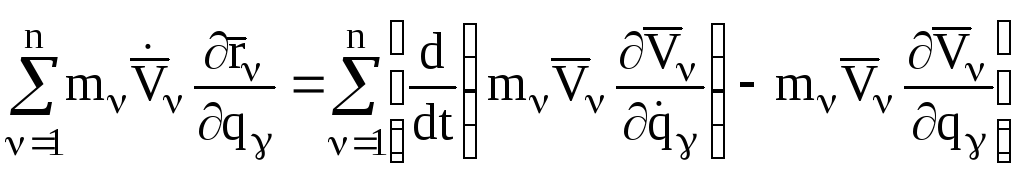. (14)

Учитывая, что

и

приведем последнее равенство к виду:

. (15)

Кинетическая энергия системы определяется формулой:

,

тогда (15) примет вид:

. (16)

Подставляя выражения (7) и (16) в уравнения (6), получим:

. (17)

(17)- уравнения Лагранжа второго рода. Число уравнений Лагранжа второго рода равно числу независимых обобщен­ных координат, т. е. числу степеней свободы этой голономной системы.

Кинетическая энергия системы при подстановке в эти уравнения должна быть предварительно выражена как функция обобщенных скоростей и координат . Это будет квадратичная функция обобщенных скоростей , в коэффициенты которой могут входить обобщенные координаты (в частных случаях кинетическая энергия может быть квадратичной функцией скоростей с постоянными коэффициен­тами). Обобщенные силы тоже могут быть в общем случае функция­ми обобщенных координат , и скоростей .Таким образом, в выражения , и могут входить обобщенные координаты и их производные . Поэтому в выражение войдут уже вторые производные . Следовательно, уравнения Лагранжа второго рода (3.18) представляют собой обыкновенные дифференциальные уравнения второго порядка относительно обобщенных координат .