13. Моменты инерции относительно пучка прямых, тензор инерции

Выбираем систему декартовых координат с началом в центре О. Проведем через начало координат произвольную ось О, образующую с осями координат Ох, Оу и Оz соответственно углы

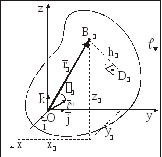
Рис. 28

На основании определения для момента инерции СМТ относительно оси O имеем:

. (1)

Для прямоугольного треугольника OD_B_ можно записать

, (2)

где ,

(3)

Здесь – единичный вектор оси О.

Преобразуем соотношение (2), с учетом формулы (3) и соотношения , следующим образом:

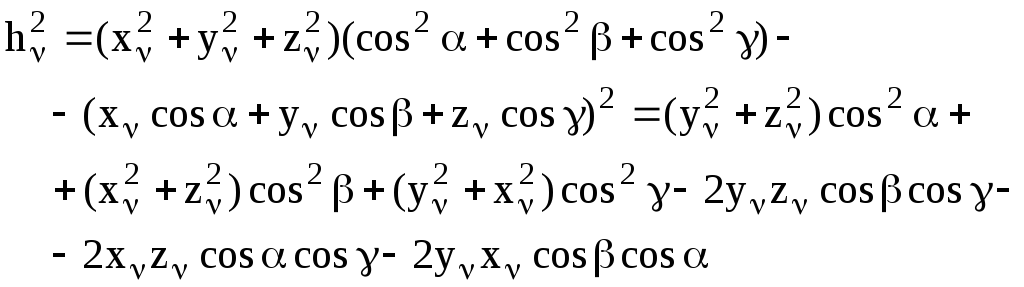(4)

Подставим соотношение (4) в соотношение (1):

(5)

Учтем, что на основании соотношений определений для осевых моментов можно записать:

(6)

где J_xx, J_yy, J_zz – моменты инерции СМТ относительно координатных осей. Величины

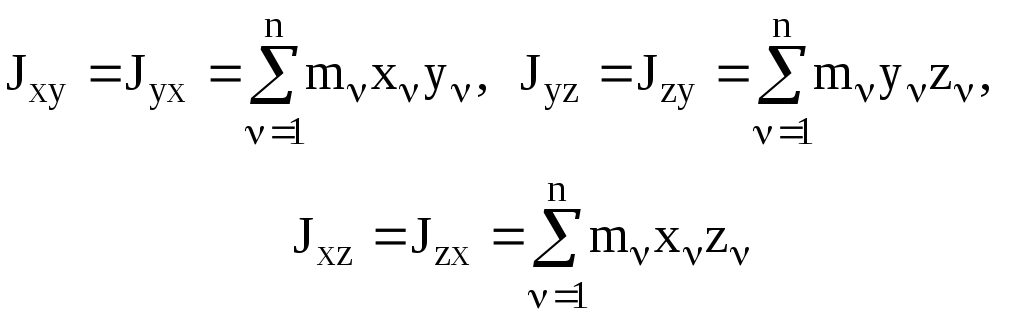(7)

называются произведениями инерции или центробежными моментами инерции СМТ.

С учетом (6) и (7) соотношение (5) примет вид:

(8)

Из равенства (8) следует, что для определения момента инерции СМТ относительно любой оси, проходящей через начало координат О, достаточно знать шесть величин J_xx, J_yy, J_zz, J_xy, J_yz, J_xz и направление этой оси, определяемое косинусами углов , , . Шесть величин J_xx, J_yy, J_zz, J_xy, J_yz, J_xz зависят от положения точки О и от направления координатных осей, так как с их изменением изменяются x_, y_, z_. Указанные величины можно расположить в виде симметричной матрицы:

, (9)

которая называется тензором инерции, элементы этой матрицы называются компонентами тензора инерции.

14 эллипсоид инерции, главные оси инерции

Для характеристики распределения моментов инерции СМТ относительно различных осей, проходящих через заданную точку, используется поверхность второго порядка – эллипсоид инерции. Для построения этой поверхности на каждой оси , проходящей через точку , откладывается вектор , модуль которого равен:

. (1)

Здесь

(2)

Выразим косинусы углов через координатывектора :

(3)

Подставив в соотношение (2) формулы (3), получим уравнение поверхности второго порядка:

. (4)

Геометрическое место концов вектора располагается на поверхности, которая называется эллипсоидом инерции. Для каждой точки O имеется свой эллипсоид инерции. Эллипсоид инерции для центра масс СМТ называется центральным эллипсоидом инерции. Оси эллипсоида инерции называются главными осями инерции. В общем случае эллипсоид инерции имеет три взаимно перпендикулярные главные оси инерции. Они являются его осями инерции.

Моменты инерции относительно главных осей инерции называются главными моментами инерции, а относительно главных центральных осей инерции – главными центральными моментами инерции.

Если уравнение эллипсоида инерции отнести к его главным осям Ox', Oy', Oz', то оно примет вид:

, (5)

где x', y', z' – текущие координаты точки, расположенной на эллипсоиде инерции, относительно главных осей инерции; – главные моменты инерции.

Центробежные моменты инерции относительно главных осей инерции равны нулю

.

15 Теорема об изменении количества движения смт

Второй основной закон динамики для -й МТ, входящей в СМТ, с учетом классификации сил, действующих на нее, можно записать в форме:

(=1, 2, ..., n). (1)

Просуммировав эти выражения и учитывая, что сумма производных равна производной от суммы, получим:

(2)

Используем формулу для главного вектора сил и учтем свойство внутренних сил:

,, (3)

где – главный вектор всех внешних сил,– главный вектор всех внутренних сил.

Количеством движения СМТ называется геометрическая сумма количеств движений МТ, входящих в СМТ:

. (4)

Подставляя выражение (3) и (4) в соотношение (2), получим теорему об изменении количества движения СМТ в дифференциальной форме:

(5)

Теорема: Производная по времени от количества движения СМТ равна главному вектору внешних сил, действующих на СМТ.

Проектируя соотношение (5) на оси декартовой системы координат, получим:

,,. (6)

Из формулы (6) следует, что производная по времени от проекции количества движения СМТ на какую-либо ось декартовой системы координат равна сумме проекций на эту же ось приложенных к СМТ внешних сил.

Умножим обе части соотношения (5) на dt:

.

Проинтегрировав это выражение, считая, что в начальный момент времени количество движения СМТ было равно , получим теорему об изменении количества движения СМТ в конечной форме:

. (7)

Здесь ,– скорость движения-й МТ в начальный момент времени, а – импульс главного вектора внешних сил или сумма импульсов внешних сил, действующих на СМТ за промежуток времениt:

. (8)

Теорема: Изменение количества движения СМТ за конечный промежуток времени равно сумме импульсов всех внешних сил, действующих на СМТ, за тот же промежуток времени.

В проекциях на оси декартовой системы координат эта теорема в конечной форме имеет вид:

,

, (9)

т.е изменение проекции количества движения СМТ за конечный промежуток времени равно сумме проекций импульсов всех внешних сил, действующих на СМТ, за тот же промежуток времени.

Следствия:

• Если , то из соотношения (5) следует, что

.

Если главный вектор внешних сил, действующих на СМТ, равен нулю, то количество движения СМТ постоянно по величине и направлению и равняется количеству движения СМТ в начальный момент времени:

. (10)

• Если (для определенности выбрана ось х), то из первого соотношения (6) следует, что

Соотношение (10) представляет собой закон сохранения количества движения СМТ.