Дополнительная часть д.1. Трубопроводы с непрерывной раздачей по длине

Предположим, что расход равномерно разбирается по пути движения, рис.Д.1.1 К такой схеме приближается работа магистральной газовой сети низкого давления вдоль улицы города, а также наружного водопровода. Допустим, что расход жидкости, раздаваемый на единице длины, равен q

q = Q/l

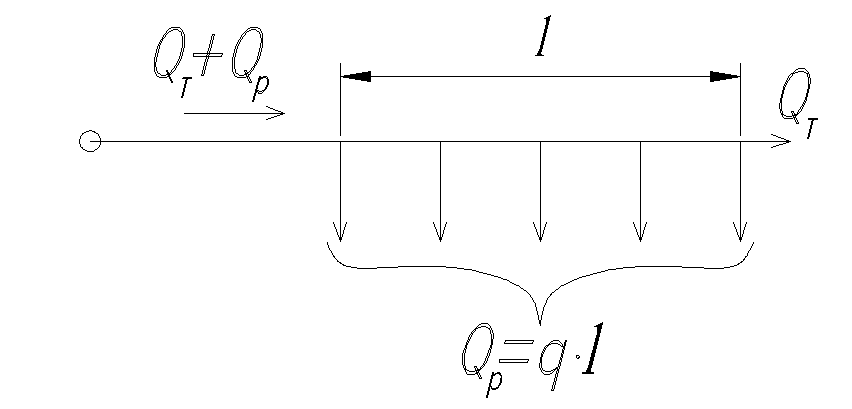
Рис. Д.1.1 Рис.Д.1.2

Тогда расход, проходящий через элементарный участок длины dxравен

Q_x = Q – q · x,

а потери напора на этом участке

откуда потери напора по всей длине трубопровода

Сравнивая полученный результат с аналогичным для потока с постоянным расходом получаем, что при равномерной раздаче расхода потери энергии в трубопроводе в три раза меньше, чем в случае транзитного расхода.

На практике обычно встречается смешанный случай, когда часть расхода Q_T проходит транзитом, а другаяQ_P отбирается вдоль пути, рис. Д.1.2. В этом случае потери энергии определяются по формуле

где расчетный расход Q_расч определяется по формуле

Д.2. Течение в трубопроводе в условиях теплообмена.

До сих пор рассматривались изотермические потоки, для которых температура, плотность и вязкость жидкости остаются постоянными на всем протяжении потока и в любой точке его поперечного сечения.

При эксплуатации систем теплоснабжения приходится встречаться с потоками жидкости, которые либо подогреваются за счет внешнего источника тепла либо охлаждаются, отдавая тепло в окружающую среду.

О

Рис.Д.2.1.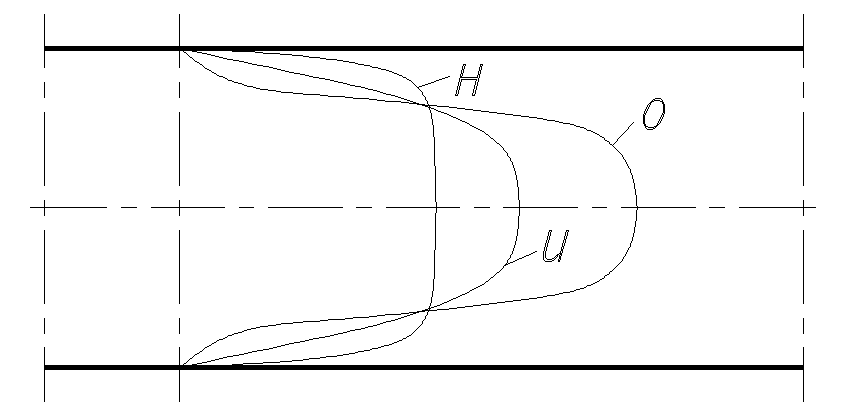

пыт и теория показывают, что распределение скоростей в поперечном сечении потока зависит от направления теплового потока. Например, при охлаждении ламинарного потока жидкости в трубе круглого сечения струйки жидкости, находящиеся вблизи стенок будут иметь более низкую температуру, чем осевая струйка; соответственно, вязкость в периферийной области будет больше, чем в центральной.

Учитывая закон внутреннего трения Ньютона и основное уравнение равномерного движения возможно получить зависимость

.

Из последнего выражения следует, что если в слое жидкости на расстоянии rот оси трубы в результате охлаждения увеличится вязкость, то соответственно уменьшиться градиент скорости. Это приведет к изменениям обычного параболического распределения скорости в поперечном сечении трубы; характер этих изменений показан на рис. Д.2.1. Криваяи относится к изотермическому течению, криваяо – к случаю остывания, криваян – к случаю нагревания. По мере продвижения жидкости по трубопроводу температура потока приближается к температуре окружающей среды и кривая распределения скоростей все меньше отличается от нормальной параболы. Скорость жидкости будет поэтому, функцией не только радиуса, но и расстояния от начального сечения.

Уравнение неразрывности будет в этом случае будет иметь вид

где L– расстояние вдоль оси потока, изменение плотности от температуры не учитывается.

Для практического применения рекомендуется зависимость

,

в которой λ_Н – коэффициент гидравлического сопротивления неизотермическом режиме, определяемый по известным формулам, ν_ср – кинематический коэффициент вязкости, соответствующий средней температуре жидкости, ν_ст – кинематический коэффициент вязкости, соответствующий температуре стенки.