|
|
|
|
x (u ,u |
|
,...,u |
|
) |
|
|
|
|
1 |
1 |
|
2 |
|
n |
|
x r(u) r(u ,u |
2 |
,...,u |
n |
) x2 (u1 |
,u2 ,...,un ) . |
1 |
|
........................ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
(u1 |
,u2 |
,...,un ) |
Если r - биективное (взаимно однозначное) отображение, то будем говорить, что задана криволинейная система координат, так как в этом случае положение точки x D однозначно определяется точкой u D1 . Если вектор-
функция r дифференцируема, то криволинейную систему координат будем называть регулярной. Заметим, что в этом случае, по теореме о производной обратной функции [раздел 2.5], обратное отображение, осуществляемое век- тор-функцией r 1 , дифференцируемо.
Система вектор-функций x r(u) r(u1 ,u2 ,...,un ) при ul const образует, как и в случае декартовых координат,
систему координатных поверхностей. Пересечения координатных поверхностей образуют координатные поверхности меньшей размерности. В частности при n 2 , отображение r r(u,v) задаёт криволинейную систему координат на плоскости, а кривые
(x, y)T r(u,C2 ) x(u,C2 )i y(u,C2 )j, (x, y)T r(C1,v) x(C1,v)i y(C1,v)j ,
образуют координатные линии. Аналогично при n 3 отображение r r(u,v, w) задаёт криволинейную систему ко-
ординат в пространстве R3 , поверхности
(x, y, z)T r(u,v,C3 ) x(u,v,C3 )i y(u,v,C3 )j z(u,v,C3 )k ,
(x, y, z)T r(u,C2 , w) x(u,C2 , w)i y(u,C2 , w)j z(u,C2 , w)k ,
(x, y, z)T r(C1,v, w) x(C1,v, w)i y(C1,v, w)j z(C1,v, w)k ,
образуют координатные поверхности, а их пересечения, то есть кривые







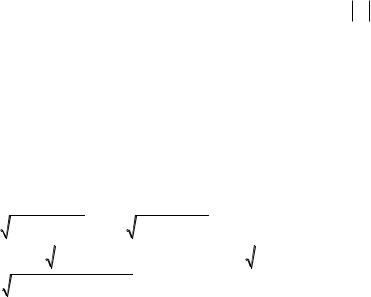




 r
r 
 du
du


 - модуль якобиана
- модуль якобиана 