
Математика (семестр 2, часть 2).-1
.pdfТомский государственный университет систем управления и радиоэлектроники
Приходовский М.А.
Математика
Учебно-методическое пособие (курс практических занятий)
2-й семестр (часть 2)
для специальности:
09.03.03 «прикладная информатика в экономике» (группа 445)
Томск
ТУСУР
2016
1
Электронное пособие составлено и скорректировано с учѐтом реального проведения практических занятий на ФСУ в группе 445 весной 2016 года.
Во втором семестре, согласно рабочей программе, на специальности 09.03.03 во второй половине весеннего семестра изучаются следующие темы:
1.Основы комплексных чисел.
2.Числовые и функциональные ряды.
3. Степенные ряды, ряды Тейлора и Лорана. 4. Ряды Фурье.
Может представлять методический интерес для преподавателей, работающих на аналогичных специальностях, как материал для планирования занятий.
2
445 ПРАКТИКА № 10 29.04.2016
Комплексные числа |
|
Задача 1. |
|
Умножить и поделить в алгебраической форме 7 i |
и 2 4i . |
Решение. Умножим эти числа. |
(7 i)(2 4i) = 14 2i 28i 4i 2 = |
||||||||||||||||||
14 4 30i |
= 10 30i . |
|
|
|
|
|
|
|
|
|
|||||||||
Поделим, с помощью умножения на сопряжѐнное: |
|
|
|
|
|||||||||||||||
|
7 i |
|
|
|
|
(7 i)(2 4i) |
14 4i 2 2i 28i |
|
14 4 26i |
|
18 26i |
||||||||
|
|
|
|
|
= |
|
|
|
= |
|
= |
|
= |
|
|
|
|||
|
2 4i |
|
(2 4i)(2 4i) |
4 16i 2 8i 8i |
4 16 |
20 |
|
||||||||||||
= |
9 |
|
13i |
= 0,9 1,3i . |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10 |
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|||||
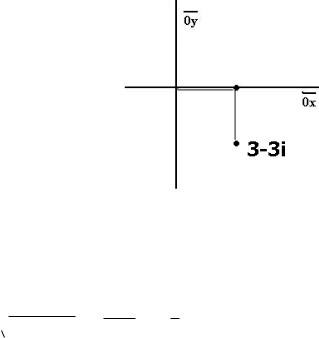
Задача |
2. |
Запишите |
число |
z 3 3i |
в |
тригонометрической и |
|||||||||||||
показательной формах. |
|
|
|
|
|
|
|
|
|
||||||||||
Решение. |
Здесь первая |
координата x |
положительна, |
вторая |
|
координата y |
отрицательна, то есть от начала координат к данной |
||||
точке нужно |
двигаться вправо и вниз, т.е. |
точка расположена в |
|||
четвѐртой четверти. |
|
|
|
|
|
Вычислим |
модуль |
и |
аргумент |
данного |
числа. |

 32 ( 3)2
32 ( 3)2 
 9 9 3
9 9 3
 2 .
2 .
3

|
y |
|
3 |
|
arctg 1 |
|
|
|
arctg |
|
|
arctg |
|
|
|
. Впрочем, также будет |
|
|
|
|
||||||
x |
|
3 |
|
|
4 |
|
||
верно принять 74 , что отличается на полный оборот 2 .
Тригонометрическая форма числа z 3 3i :
(cos i sin ) = 3 |
|
|
|
|
|
|
|
|
|
||||||||
2 cos |
|
i sin |
. |
|||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|||
i
Показательная форма: z ei = 3
 2e 4 .
2e 4 .
Задача 3. Разделить |
2 2i |
двумя способами: |
|
1 i |
|
1)с помощью умножения на сопряжѐнное число.
2)в показательной форме.
Решение. |
|
1) |
|
2 2i |
= |
( 2 2i)(1 i) |
= |
4i |
|
2i . |
|
|
|
|
|
||||||||||
|
|
|
1 i |
|
|
(1 i)(1 i) |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
i3 |
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2i |
|
2 2 e |
4 |
|
|
|
|
|
|
i |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 e |
3 |
|
|
2 e |
2 = 2 cos |
|
i sin |
|
= |
|
|||
2) |
|
= |
|
|
|
|
|
|
|
|
= |
|
4 |
4 = |
|
|
|
|
2i |
||||||
1 i |
|
|
|
|
ei 4 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
||||
Задача 4. Возвести в степень в алгебраической и показательной |
|
||||||||||||||||||||||||
форме: 1 i 4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Перейдѐм к показательной форме, для этого сначала найдѐм |
||||||||||||||||||
модуль и аргумент числа |
1 i с помощью чертежа. Число в 1-й |
|
|
|||||||||||||||
четверти, угол 45 градусов. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
i |
4 |
|
1 i |
|
|
|
i sin |
= |
2e 4 . По формуле Муавра, |
2e 4 |
|
= |
|||||||||
|
2 cos |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 ei |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
4 4 |
= 2 2 ei |
4 4 = 4ei |
= 4 cos i sin = 4 1 0i = 4 . |
|
|
||||||||||||
2 |
|
|
||||||||||||||||
4
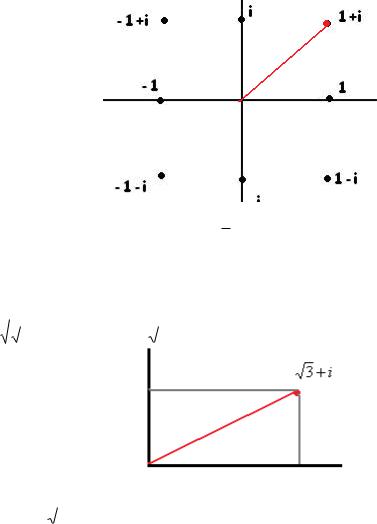
Чертѐж, показывающий, расположение 1 i на плоскости, это число выделено красным цветом:
Задача 5. Возвести в степень 
 3 i 18 .
3 i 18 .
Решение. Аналогично прошлой задаче, сначала переводим в
показательную форму. Угол здесь 30 градусов, то есть |
|
, модуль |
|||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
i = 2ei |
|
|
|
|
|
|
2 12 2 . Итак, |
|
|
|
|||
|
|
|
|
6 . |
|
|
|||
|
|
3 |
3 |
|
|
||||
|
|
|
|
i |
|
18 |
i |
|
18 |
|
|
Тогда |
3 i 18 |
= |
2e |
6 |
|
= 218 e |
6 |
= |
218 ei3 |
= 218 cos 3 i sin 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь можем отнять полный оборот 2 , косинус и синус при этом не меняются. тогда получим 218 cos i sin = 218 1 i0 = 218 =21028 1024 256 = 262144.
5
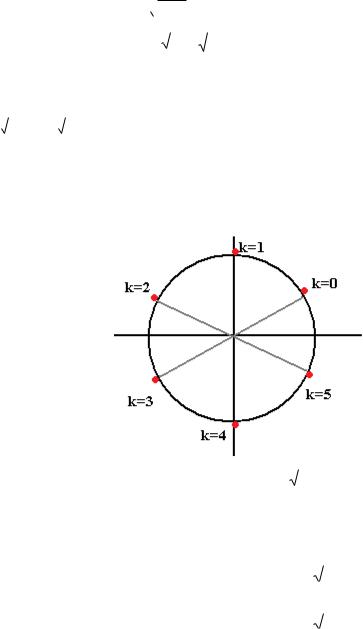
Задача 6. Вычислить 6  64 .
64 .
|
|
|
|
|
2 k |
|
|
|
|||
Решение. По формуле n z n cos |
|
||||
|
|
|
|
|
n |
i sin |
2 k |
|
|
. |
|
|
n |
|
Сначала запишем число в тригонометрической форме.
64 64(cos i sin ) . Тогда
|
|
|
|
|
|
|
|
|
|
2 k |
|
|
2 k |
|||
6 64 |
6 |
|
|
|
|
i sin |
||||||||||
64 cos |
|
|
|
|
= |
|||||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
6 |
|
|
|
|
k |
|
|
|
|
|
k |
|
|
|||||
2 cos |
|
|
|
i sin |
|
. Начертим окружность радиуса 2 и |
||||||||||
|
6 |
|
|
3 |
|
6 |
|
|
|
|
|
|||||
|
|
|
|
|
|
3 |
|
|
||||||||
отметим там 6 точек, первой соответствует угол 300, остальные больше на 600 , 1200 и так далее.
|
|
|
|
|
|
|
z |
|
|
|
|
|
|||||
k 0 |
|
3 i |
|
||||||||||||||
z 2 cos |
|
|
i sin |
|
|
|
|
||||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
6 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
z 2i |
|
|
|
|
|
|||||||
k 1 z 2 cos |
|
|
i sin |
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||
k 2 z 2 cos |
|
|
|
i sin |
|
|
|
z |
3 |
i |
|||||||
|
|
|
|
||||||||||||||
|
|
|
6 |
|
|
6 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
7 |
|
|
7 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||
k 3 z 2 cos |
|
|
|
i sin |
|
|
|
z |
3 |
i |
|||||||
|
|
|
|||||||||||||||
|
|
|
6 |
|
|
6 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||
6
|
|
|
|
|
|
|
|
|
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
k |
4 z |
2 cos |
|
|
i sin |
|
|
|
|
|
z 2i |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
6 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
11 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
k |
5 z |
2 cos |
|
|
|
i sin |
|
|
|
|
z |
|
3 |
i . |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
6 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Задача 7. Дано z 2 i |
. Найти e z . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 i |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2 |
|
|
i |
|
|
|
2 |
3 |
|
|
1 |
|
|||||||||||||||
Решение. |
e |
6 |
e |
|
e |
6 = e |
cos |
|
|
i sin |
|
|
= e |
|
|
|
|
|
|
|
i |
= |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
6 |
|
|
|
2 |
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
e2 |
|
|
|
|
e2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задача 8. Найти все значения Ln(i) . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Решение. |
По формуле Ln(z) ln i( 2k) |
|
( k Z ): |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 k |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Ln(i) = ln(1) i |
|
|
2 k |
= 0 i |
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Задача 9. Начертить область, удовлетворяющую условиям:
Re( z) 0, Im( z) 0 .
Решение. Эти множества можно записать так: x 0, y 0 .
Первое есть правая полуплоскость, второе - перхняя полуплоскость.
В пересечении получается первая четверть. Чертѐж очевиден: заштриховать 1-ю четверть.
Задача 10. Начертить область, удовлетворяющую условиям:
{Im(z) 1, z i 2}.
Решение. Первое множество соответствует y 1 на плоскости, обозначено зелѐным цветом. Второе это круг радиуса 2 вокруг точки i , обозначено красным цветом. Пересечение двух множеств, то есть именно то, что надо найти, показано жѐлтым цветом.
7

Домашняя задача.
Возвести в степень в показательной форме: 1 i 6 Ответ 8i.
Тема: Числовые ряды.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 11. |
|
Найти сумму ряда. |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
n |
2 |
6n |
8 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. |
Чтобы разбить на группы слагаемых, часть из которых |
|
|
|
||||||||||||||||||||||||||||||||||||||
будет взаимно скращаться, сначала разложим знаменатель на |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
множители: |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
затем надо разбить на |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
n2 6n 8 |
(n 2)(n 4) |
|
|
|
|
|||||||||||||||||||||||||||||||||||
простейшие дроби. |
|
|
|
|
2 |
|
|
|
|
|
A |
|
|
|
|
B |
|
= |
A(n 4) B(n 2) |
, |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(n 2)(n 4) |
|
|
n 2 |
|
|
n 4 |
|
(n 2)(n 4) |
|
|
|
||||||||||||||||||||
откуда A(n 4) B(n 2) 0n 2, |
|
An Bn (4A 2B) 0n 2 , |
|
|
|
|
||||||||||||||||||||||||||||||||||||
получаем систему |
|
A B 0 |
|
, отсюда |
|
A 1, B 1. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4A 2B 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
1 |
|
|
|||||
Тогда ряд можно представить так: |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
2 |
|
|
6n 8 |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 5 |
n |
|
|
|
n 5 n 4 |
|
n |
|
2 |
||||||||||||
|
1 |
|
1 |
|
1 |
|
|
|
1 |
|
|
1 |
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
Здесь для любого |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
3 |
|
2 4 |
|
|
|
3 5 |
|
|
4 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
знаменателя, начиная от 3 и выше, всегда есть отрицательная дробь с таким знаменателем, а через 2 шага точно такая же положительная.
Таким образом, сокращается всѐ, кроме 1 12 32 . Ответ: 32 .
8
Выяснить сходимость по признакам сравнения или интегральному признаку Коши:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Задача 12. Выяснить, сходится или расходится ряд |
|
. |
|
|
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 2 |
n ln n |
|
|
||||
Решение. По интегральному признаку Коши, можем рассмотреть |
|
||||||||||||||||||||||||||||
несобственный интеграл, эквивалентный данному ряду по |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
1 |
1 |
|
|
|
1 |
|
ln x = |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
= |
= |
|
|
|
|
|
|
. |
||||||||||||||
сходимости. |
|
|
|
dx |
|
|
|
|
|
dx |
|
d |
ln(ln x) |
2 = |
|||||||||||||||
|
|
|
|
2 |
x ln x |
|
2 |
|
ln x x |
|
|
2 |
ln x |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Интеграл расходится, значит, и ряд расходится. |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Задача 13. Выяснить, сходится или расходится ряд |
|
|
|
. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
3 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 3 n |
|
ln n |
|
|
|||
Решение. Заметим, что |
|
|
1 |
|
|
1 |
для любого n 3 . |
Тогда ряд (по |
|||||||||||||||||||||
|
n3 ln n |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
признаку сравнения) можно ограничить сверху другим рядом, |
|
|
|||||||||||||||||||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
|
, который, в свою очередь, сходится, так сходится |
|||||||||||||||||||||||||
|
3 |
3 |
|||||||||||||||||||||||||||
n 3 n |
ln n |
|
n 3 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
эквивалентный ему несобственный интеграл |
dx (заменяем по |
|
|||||||||||||||||||||||||||
3 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интегральному признаку Коши). Итак, ответ: ряд сходится (добавим, что сходится абсолютно, так как все слагаемые и так положительны).
|
|
|
|
|
|
|
|
|
|
|
||||
Задача 14. Выяснить, сходимость ряда |
|
ln n |
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
n 3 n |
|
|
|
|
|
||||
Решение. По признаку сравнения в непредельной форме, |
ln n |
|
1 |
, |
||||||||||
n |
n |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
таким образом, этот ряд получается больше, чем некоторый |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
расходящийся |
ln n |
> |
1 |
. Гармонический ряд |
1 |
расходится, |
||||||||
|
|
|
||||||||||||
n 3 n |
n 3 n |
|
|
n 3 n |
|
|
|
|
|
|||||
9

ln n
это было доказано в лекциях ранее. Поэтому ответ:
n 3 n
расходится.
Выяснить сходимость по признаку Даламбера:
3n
Задача 15. Выяснить, сходимость ряда .
n 1 n!
Решение. Запишем предел отношения последующего (n+1) члена ряда к предыдущему (n). Модули здесь не особо нужны, так как все члены ряда и так положительны, т.е. если сходимость есть, то она заодно и абсолютная.
|
| a |
n 1 |
| |
|
|
|
a |
n 1 |
|
|
|
3n 1 |
|
3n |
|
|
|
3n 1 n! |
|
|
3 |
|
|
|||||
lim |
|
|
|
lim |
|
|
= lim |
|
|
|
: |
|
|
= |
lim |
|
|
|
|
= |
lim |
|
|
=0. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||||||||||||
n | an | |
|
|
n an |
|
|
|
(n 1)! |
|
|
|
|
n 3 |
(n 1)! |
|
n n 1 |
|
||||||||||||
|
|
|
n |
|
n! |
|
|
|
|
|||||||||||||||||||
Итак, |
q 0 1, ряд сходится (абсолютно). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
n |
(n 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Задача 16. |
|
( 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
n 1 |
|
2n n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Запишем предел отношения модуля (n+1) члена ряда к модулю n-го. При этом мы отбрасываем знакочередование.
|
|
| a |
n 1 |
| |
|
|
|
(n 2) |
|
(n 1) |
|
|
|
(n 2) |
2n n! |
|
||||||||||
lim |
|
|
= |
lim |
|
|
|
|
|
: |
|
|
|
|
= |
lim |
|
|
|
|
|
|
= |
|||
|
|
|
|
|
n 1 |
|
|
|
n |
|
|
n 1 |
|
|
|
|||||||||||
n | an | |
|
|
|
2 |
(n 1)! |
|
2 |
n! |
|
|
|
2 |
(n 1)! |
(n 1) |
|
|
||||||||||
|
|
n |
|
|
|
|
|
|
n |
|
|
|
||||||||||||||
lim |
|
n 2 |
lim |
1 |
|
|
= 1 0 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
n n 1 n 2(n 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Итак, q 0 1, ряд сходится (абсолютно).
10
