Математика-2-й семестр (курс лекций)

x t3 ,

y cos2 t,

2.9. Производная функции, заданной неявно

(предполагая её существование):

131

Аналогично может быть получено выражение для производной третьего, четвертого порядков и т.д.

Производную второго порядка y можно найти по другому,

xx

дважды продифференцировав тождество (x, y(x)) 0 по x :

Рассмотрим несколько примеров, иллюстрирующих сказанное.

Пример 1. Найти y , если y задана неявно уравнением

x

y2 x2 y 2xy 0.

Дифференцируя обе части по x , с учетом, что y y(x) ,

имеем 2yy 3x2 y x3 y 2y 2xy 0.

Разрешая это уравнение относительно y , получаем

Сравните с результатом, полученным по формуле (2.20).

Пример 2. Найти y для функции, заданной неявно уравне-

xx

нием y2 x2 y 2xy 0.

Дифференцируя обе части по x , имеем

(2y x3 2x) y 3x2 y 2y 0.

x

132

цию z(x, y) . Тогда (x, y, z(x, y)) – сложная функция переменных x, y , а (x, y, z(x, y)) 0 – тождество. Дифференцируя обе части этого тождества по x , получаем

Для функции трех и большего числа переменных вывод формул для вычисления производных проделайте самостоятельно.

Для отыскания z продифференцируем дважды тождество

xx

(x, y, z(x, y)) 0 :

133

Дифференцируя обе части тождества (2.21) по y , имеем

Аналогично получаем выражение для второй производной по y

Подобным образом могут быть вычислены частные производные любого порядка для функции, заданной неявно.

134

или, с учетом выражения для z y

135

Пусть система двух уравнений

ции z1(x, y) , z2 (x, y) . Тогда в D имеем два тождества

то по формулам Крамера из (2.23) находим

136

Если тождества (2.22) продифференцировать по переменной y ,

то аналогично можно найти частные производные z1 , z2 .

y y

Пример 5. Найти, z1 , z2 , если z1 и z2 заданы неявно сис-

x x

темой уравнений

x y z1 z2 0,

x sin z2 y sin z1 0.

Дифференцируя эти тождества по x , получаем систему уравнений

из которой по формулам Крамера находим

Таким же способом можно найти частные производные функций z1, z2 ,..., zm по переменным x1, x2 ,..., xn , если эти функции заданы неявно системой уравнений

2.10. Геометрический и механический смысл производной

Приложение производной в геометрии и механике основано на её геометрическом и механическом смыслах.

137

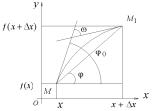
Пусть f – дифференцируемая функция одной переменной. Построим график функции f и проведем секущую, соединяю-

щую точки M 0 (x, f (x)) и M (x x, f (x x)) . Определение. Предельное положение секущей M 0M ,

когда точка M стремится к точке M 0 , называется касательной к кривой в точке M 0 .

Тангенс угла , изображенного на рисунке, равен

Таким образом, геометрический смысл производной заключает-

параллельный касательной к кривой r(t) в точке r(t0 ) , причём вектор r (t) направлен в сторону возрастания аргумента t . Ана-

логично, в случае плоской кривой r r(t) (x(t), y(t))T вектор

138

r (t) (x (t), y (t))T параллелен касательной к кривой r(t) в точ-

ке r(t0 ) .

Поскольку параметрическое задание кривой

эквивалентно векторному r r(t) (x(t), y(t))T , то из сказанного

Если в каждой точке графика функции провести касательную, то эта касательная при перемещении точки касания будет вращаться. Введем понятие средней кривизны кривой на участке MM1 как отношение угла между касательными в точках

Mи M1 к длине дуги участка кривой MM1 .

Кривизной графика функции в точке M называют число

K : K lim .

0

Можно показать, что для кривой, заданной векторно уравнением r r(t) , кривизна находится по формуле

K [r (t), r (t)] , r (t) 3

где [r (t), r (t)] – векторное произведение [1] векторов r (t) и r (t) .

Для плоской кривой, заданной параметрически, последняя формула принимает вид

139

Если функция f (x) имеет конечную вторую производную,

то

Как видим, величина второй производной определяет степень искривленности графика функции.

Скалярная функция скалярного аргумента отображает отре-

определения дифференцируемости следует, что для дифференцируемой функции эта длина отличается на бесконечно малую

образом, модуль производной есть коэффициент искажения длины при дифференцируемом отображении из R в R .

Вектор-функция

рядка малости, чем u и v . Можно показать, что площади

140