Математика-2-й семестр (курс лекций)

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Пример 12. В интеграле

подынтегральная

Пример 12. В интеграле

подынтегральная

..pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

11.03 Mб

Скачать

☆

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 2728 / 3528 29 30 31 32 33 34 35 > Следующая >>>

ды

можно сделать

про

несобственные

интегралы

(x a)

(b x)

Интегралы

используются в

(x a)

(b x)

признаке сравнения в качестве эталонных.

Пример 2. В интеграле

подынтегральная функ-

ln x

ция имеет особенность в точке x 1, поэтому

ln x

lim

lim 2

ln x

2 .

lim

ln e 2

ln(1 )

Следовательно, интеграл сходится и его значение равно

Пример 3. В интеграле dx подынтегральная

0 x ln x

функция имеет особенность в точках x 0

и x 1, поэтому ин-

теграл

разбиваем

на

сумму

двух,

например,

0,5

Для

первого

из них

x ln x

ln x

0,5

d ln x

0,5

lim

lim 2

ln x

0 x ln x

ln x

) .

lim

ln 0,5

Следовательно, интеграл рас-

ходится, и поэтому исходный интеграл также расходится.

1/ e

Пример 4. В интеграле

подынтегральная функ-

x ln 2

ция

имеет

особенность

точке

x 0 ,

поэтому

271

1/ e			dx						1/ e d ln x																	1			1/ e							1					1
1/ e			dx						1/ e d ln x																	1			1/ e							1					1
								lim
		x ln		2		x		lim			ln			2	x				lim						ln x						lim					ln	1									1
0		x ln				x		0			ln				x				0						ln x						0					ln	e			ln
0																			0												0						e
Следовательно, интеграл сходится и его значение равно 1.
																																						1					dx
					Пример					5.				Выясним						сходимость											интеграла												dx				.


																																						0			1 x2
Подынтегральная функция имеет особенность в точке																																										x 1.
																1			dx							1					dx														10
Поэтому																					lim												lim arcsin x


																				2
																		1 x		2			0							1 x		2			0
																0		1 x						0						1 x
lim(arcsin(1 ) arcsin 0) .																							Следовательно,													интеграл										схо-
	0																	2
дится и его значение равно .
																		2
																																				2			dx
					Пример 6. Выяснить сходимость интеграла																																		dx					.


																																							x 1
																																				1
					Подынтегральная функция имеет особенность в точке
x 1.												По										определению																				имеем
2			dx						2			dx														2								2
2									2																									2


							lim									lim 2					x			1			2				x 1)					2		.			Следо-
							lim									lim 2					x			1			2				x 1)					2		.			Следо-
			x 1					0				x 1						0								1								1
			x 1					0				x 1						0								1
1								1
вательно, интеграл сходится и его значение равно 2.
																																				2			dx
					Пример 7. Выяснить сходимость интеграла																																		dx							.


																																							2 x
																																							2 x
																																				1
					Подынтегральная функция имеет особенность в точке
x 2 .												По										определению																				имеем
2			dx					2					dx				lim 2											2
			dx					lim					dx										2 x								2 .				Следовательно,


1			2 x					0	1				2 x						0									1
1									1

интеграл сходится и его значение равно 2.

Пример 8. Выяснить сходимость интеграла dx .

1 3 2 x

272

		Подынтегральная функция имеет особенность в точке
x 2 .			Поэтому					разбиваем						интеграл			на		сумму		двух
3		dx		2	dx			3		dx
		dx			dx					dx		.	Для		первого			из		них	имеем

3				3				3
3		2 x		3	2 x			3		2 x
1				1				2
2		dx			2		dx						3				2	3
																	2
																2
			lim						lim					3 (2	x)				.	Аналогично
	3		lim			3			lim					3 (2	x)				.	Аналогично
1		2 x		0	1		2 x				0		2				1	2
1					1												1

доказывается сходимость второго слагаемого. Следовательно, исходный интеграл сходится.

Аналогично случаю несобственных интегралов первого рода формулируются и доказываются критерий Коши и признаки сравнения для несобственных интегралов второго рода.

Теорема 4.15. (Критерий Коши). Несобственный интеграл второго рода сходится тогда и только тогда, когда для вся-

кого 0 существует	0 такое, что для всех		1, 2	вы-
	b 2
	b 2
полняется неравенство	f (x)dx	.
	b 1

Доказательство этого результата опустим.

Теорема 4.16. Пусть для всякого b x b выполнено

	b
неравенство 0 f (x) g(x) . Тогда если интеграл	g(x)dx схо-
	a
b		b
дится, то интеграл f (x)dx сходится, а если интеграл		f (x)dx
a		a

расходится, то интеграл g(x)dx расходится.

Доказательство аналогично случаю несобственного интеграла первого рода.

273

Теорема 4.17. Если f (x) и g(x) - бесконечно большие

одного порядка роста, то есть lim f (x) K 0, , то интегралы

x b g(x)

b b

f (x)dx и g(x)dx либо оба сходятся, либо оба расходятся.

a a

Доказательство аналогично случаю несобственного интеграла первого рода.

Замечание. После изучения теоремы 4.17 может сложиться впечатление, что для сходимости несобственного интеграла второго рода, в том числе и абсолютной, необходимо, чтобы подынтегральная функция была бесконечно большой при x b . То, что это не так, показывает следующий пример.

Пусть функция

f (x) 0 ,

lim f (x)

интеграл

x b

f (x)dx

сходится. Пусть

xn n 1

–

возрастающая последова-

тельность точек интервала

(a,b) , сходящаяся к точке b . Возь-

мем функцию (x) , график которой на отрезке [a, x1 ]

совпадает

с графиком функции f (x) , а на интервале (x1,b)

состоит из от-

резков прямых, соединяющих

точки

x2k 1, 0 ,

x2k , f x2k ,

x2k 1, 0 ,

k 1, 2,... .

Функция

(x)

не

является бесконечно

большой,

так

как

lim (x)

не

существует

( lim x2k 1 0, lim x2k ).

x b

По

теореме 4.16,

интеграл

(x)dx сходится, так как по построению 0 (x) f (x) .

Пример 9. Для интеграла

подынте-

x 2 3 3 x2

гральная функция имеет особенность в точках x 2 и x 3 . Точки x 3 в промежуток интегрирования не входят. По-

274

этому, находя порядок роста этой функции относительно

x 2

имеем

(x 2)

если 0,5;

lim

если 0,5;

x 2

3 x

x 2

если 0,5.

Таким образом, порядок роста равен 0,5, и интеграл схо-

дится.

Пример 10. В интеграле

подынтеграль-

x 1 3

9 x2

ная функция имеет особенность в точках x 1 и x 3 . Точки

x 1 и	x 3 в промежуток интегрирования не входят. Поэто-
му, находя порядок роста этой функции относительно																											1		,
му, находя порядок роста этой функции относительно																											3 x		,
имеем
						lim				(3 x)

										x 1		9 x
						x 3					3				2
													,				если				1			;
																					1
			(3 x)																		3
	lim		(3 x)									1				, если						1
												1										1			;
																						3
		x 1			3 x			3					2		6							3
	x 3	x 1		3	3 x		3	3	x				2	3	6					1
																	если									.
																	если									.
												0,								3
																				3

	Таким образом, порядок роста равен																1	, и интеграл схо-
	Таким образом, порядок роста равен																	, и интеграл схо-
																3
дится.
																			1
																			1				x2
																							x2
	Пример 11. Выясним сходимость интеграла																			sin x								dx .
	Пример 11. Выясним сходимость интеграла																		0									dx .
																			0

Подынтегральная функция имеет особенность в точке x 0 . Находя порядок роста этой функции относительно 1x ,

имеем

275

если 1,5;

sin x x

lim

если 1,5;

x 0

если 1,5.

Таким образом, порядок роста равен 1,5, и интеграл расходится.

функция имеет особенность в точке x 0 . Находя порядок роста этой функции относительно 1x , имеем

										,			если		2			;
										,			если					;
					3 sin x x			3 sin x x						3
														3
				lim			lim			1,			если			2			;
						x										3
																3
				x 0			x 0 3 x 3 x2							2
											0,		если							.
											0,		если				3			.
		Таким образом, порядок роста равен										2	, и интеграл схо-
		Таким образом, порядок роста равен									3		, и интеграл схо-
											3
дится.
		Пример			13.		Выясним		сходимость					интеграла
1
1	ln 1	5	x
	ln 1	5	x	dx.
		x		dx.
0		x
0

Подынтегральная функция имеет особенность в точке

x 0 . Находя порядок роста этой функции относительно

имеем

если 0,8;

ln 1 5 x x

lim

если 0,8;

x 0

5 x 5 x4

если 0,8.

Таким образом,

порядок роста равен

0,8 , и интеграл

сходится.

276

Пример

14. В

интеграле

подынтегральная

функция имеет особенность в точке

x 0 . Находя порядок

роста этой функции относительно

1 , имеем

если 0,5;

e x

1 x

e x 1 x

lim

если 0,5;

x 0

если 0,5.

Таким образом, порядок роста равен 0,5 , и интеграл сходится.

Пример 15. Выяснить сходимость интеграла dx .

0 x (x 1)

Подынтегральная функция имеет особенность в точках x 0 и x 1. Обе входят в промежуток интегрирования. Разбиваем интеграл на два

0,5

x (x 1)

0,5

Первый из этих интегралов сходится, так как порядок

роста подынтегральной функции при

x 0

относительно

равен 12 , а второй расходится, так как порядок роста подынте-

гральной функции при x 1 относительно	1	равен 1. По-

	1 x
	1 x
этому интеграл расходится.

4.7. Приложения определённого интеграла

4.7.1. Вычисление площадей плоских фигур

Пусть f (x) 0	для x [a,b]. Рассмотрим криволиней-
ную трапецию, ограниченную		кривыми	y 0, x a, x b ,
y f (x) . Разобьём	отрезок	[a,b] на	части точками
	277

a x0 x1 ... xn b , выберем внутри каждого элементарного отрезка [xi , xi 1 ] по точке i [xi , xi 1 ] . Заменим криволинейную


трапецию,		ограниченную	линиями
y 0, x xi , x xi 1, y f (x) ,			прямоуголь-
ником	y 0, x xi , x xi 1,		y f ( i ) .
Площадь		этого прямоугольника		равна
f ( i )(xi 1	xi ) f ( i ) xi и, если f			- не-

прерывная функция, то при достаточно малом xi близка площади заменяемой

трапеции. Просуммировав, получим, с одной стороны, приближенное значение площади криволинейной трапеции, с другой

			n 1
	стороны, интегральную сумму		f ( i ) xi
			i 0
		b
	для интеграла	f (x)dx . Переходя к преде-
		a
	лу при увеличении числа точек разбиения,
	получаем площадь S исходной			криволи-
		b
	нейной трапеции S f (x)dx .
		a
Назовём трапецию простейшей областью, если она огра-
ничена	кривыми x a, x b, y f1 (x), y f2 (x)		и	для	всех
x [a,b]	выполнено неравенство	f1 (x) f2 (x) . Нетрудно			ви-

			b
деть, что для простейшей области S ( f2 (x) f1 (x))dx .
			a
	Аналогично, если 1		( y) 2 ( y) для всех y [c, d ] , то
для	криволинейной трапеции, ограниченной			кривыми
y c, y d,		x 1 ( y), x 2	( y) (простейшей области	второго
типа),	имеем

S ( 2 ( y) 1 ( y))dy .

278

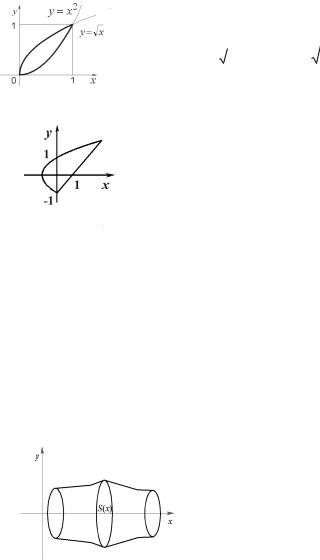
В общем случае плоскую область разбивают на простейшие области рассмотренных выше типов.

Пример 1. Найти площадь фигуры, ограниченной ли-

ниями

y x2

x y2 .

Эти кривые пересека-

ются в точках

A(0,0)

и B(1,1) . Поэтому

1 .

S (

2 )dx

Пример 2. Найти площадь фигуры, ограниченной ли-

ниями

y2 2x 1 и

x y 1 0 .

Эти кривые

пересекаются в точках

A(0, 1)

и B(4,3) . В

данном случае лучше рассматривать простей-

шую область второго типа. Поэтому

y2 1

y 1

Пример 3. Найти площадь криволинейной трапеции, ог-

раниченной линиями

x 2 ,

x 1,

y 0 ,

y e

. В данном

случае

S e

dx e

dx ex dx e x dx

0 e x

1 1 e 2 e 1 1 2 e 1 e 2 .

4.7.2. Вычисление объёмов

Пусть область такова,

что для x [a,b]

известна пло-

щадь

S(x) сечения

плоскостью

x const. Тогда,

заменяя объём об-

ласти, заключенной между плоско-

стями

x xi ,

x xi 1 ,

на объём ци-

линдра

S( i ) xi ,

где i

- некоторая

279

						b
точка отрезка [xi , xi 1]получаем V S (x)dx .
						a
		Для тел, полученных вращением криволинейной трапе-
				ции	a x b, 0 y f (x)				вокруг оси
						b		b
				OX , имеем V y 2 dx f 2 (x)dx . Ес-
						a		a
				ли эту трапецию вращать вокруг оси OY ,
									b
				то можно показать, что V 2 xf (x)dx .
									a
		Аналогично для тел, полученных вращением криволи-
нейной трапеции				c y d, 0 x ( y) вокруг оси OY ,						имеем
	d		d
V x2dy 2 ( y)dy .					Если эту	трапецию		вращать		вокруг
	c		c
				d
оси OX , то			V 2 y ( y)dy .
				c
		Пример		1.	Трапеция	ограничена			кривыми

y	x, y 0, x 1. Вычислить объём тела, полученного враще-
нием этой трапеции вокруг оси OX.
		Подставляя в формулу, получаем
					1	1
				V f 2 (x)dx xdx
				V f 2 (x)dx xdx			2
					0	0	2
					0	0
		Пример		2.	Трапеция	ограничена			кривыми
y x, y 0, x 1.				Вычислить объём тела, полученного вращени-
ем этой трапеции вокруг оси OY.
		Подставляя в формулу, получаем
					1	1		2 .
				V 2 xf (x)dx 2 x2 dx				2 .
					0	0		3

280

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 2728 / 3528 29 30 31 32 33 34 35 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023641.56 Кб2Математика (семестр 2, часть 2).-1.pdf
#
05.02.2023938.68 Кб2Математика (семестр 2, часть 2)..pdf
#
05.02.2023722.47 Кб4Математика 3 семестр..pdf
#
05.02.20231.9 Mб12Математика для гуманитарных, экологических и экономико-юридических специальностей. Часть 1.pdf
#
05.02.20234.98 Mб3Математика для гуманитарных, экологических и экономико-юридических специальностей. Часть 2.pdf
#
05.02.202311.03 Mб8Математика-2-й семестр (курс лекций)..pdf
#
05.02.20234.95 Mб4Математика-3-й семестр(курс лекций)..pdf
#
05.02.20231.56 Mб2Математика. Дополнительные главы.pdf
#
05.02.2023984.92 Кб12Математика. Математический анализ.pdf
#
05.02.20232 Mб4Математика.-1.pdf
#
05.02.20232.61 Mб3Математика.-2.pdf