
нахождения коэффициента |
k |
(2) |
вместо (5.39), |
|
|||
|
1 |
|
|
правильности определения коэффициентов 0 |
, k |
так
0 и
и
k |
(2 |
|
|
1 |
|
)
для проверки
.
Пример |
5.1. На |
входе |
нелинейного |
элемента, имеющего |
||
статическую |
квадратичную |
зависимость |
x = ( y) = ky |
2 |
между |
|
|
||||||
входным и |
выходным |
сигналом, действует случайный |
сигнал |
|||
|
|
|
|
|
|
|
Y (t) = my + Y (t) , имеющий |
нормальный |
закон распределения. |
||||
Определить эквивалентные статистические коэффициенты усиления
|
|
и k |
(2) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1. Поскольку характеристика |
нелинейного |
|
элемента является |
|||||||||||||||||||
четной, то в соответствии с (5.25) функция 0 |
равна |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
= m |
|
= M[ X (t)] = M[kY |
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
(t)] |
= M[k{m |
|
+Y (t)}] = |
|
||||||||||||
|
|
|
|
|
|
0 |
x |
|
y |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= k(my |
+D y ) = kDy (1+ my / Dy ) . |
|
|
|||||||||||
|
|
2. На основании (5.40), дифференцируя полученное выражение |
||||||||||||||||||||||
для |
|
|
определяем коэффициент k |
( |
2) |
|
: |
|
|
|
|
|
|
|
||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
k |
(2) |
= d 0dmy = 2kmy . |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
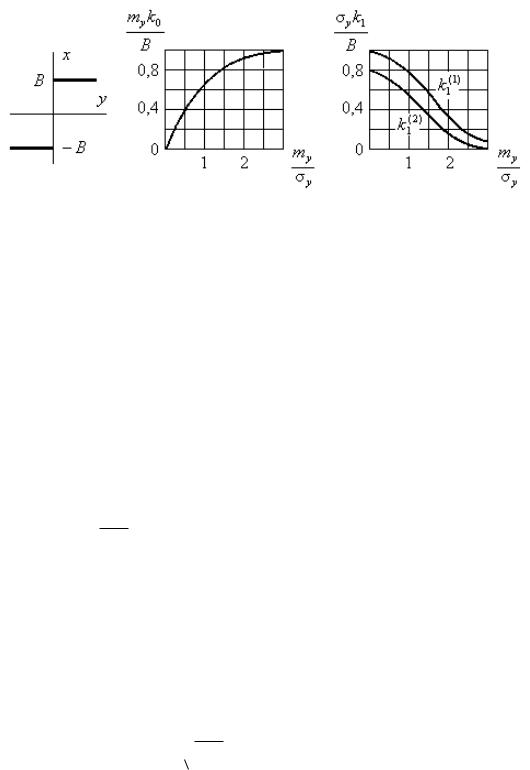
Пример 5.2. На входе нелинейного элемента типа идеального |
||||||||||||||||||||||
реле (рис. 5.7, а) с характеристикой |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
x = ( y) = B sign y = |
|
B |
при |
|
y 0; |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− B |
при |
|
y |
0, |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
действует случайный сигнал Y (t) = my + Y (t) , |
имеющий нормальный |
|||||||||||||||||||||||
закон |
|
|
распределения. Определить |
|
эквивалентные статистические |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
k (1) |
k (2) |
|
коэффициенты усиления нелинейного элемента |
|
0 |
, 1 , |
1 |
. |
|||||||||||||||||||
127
а |
б |
в |
Рис. 5.7
Решение. Для вычисления коэффициентов статистической
линеаризации достаточно знать математическое ожидание |
my |
и |
||
дисперсию |
Dy |
случайного процесса на входе нелинейного элемента и |
||
значения функции Крампа для аргументов, определяемых через |
my |
и |
||
Dy : |
|
|
|
|
|
|
x |
|
|
|
|
Ф(x) = (1/ 2π) e− z 2 / 2dx , |
(5.41) |
|
|
|
0 |
|
|
где z = ( y − m y )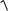
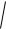 Dy .
Dy .
|
|
Вычисленные |
по приведенным формулам |
||
графики |
коэффициентов k0 = k0 (my , Dy ) , k1(1) |
||||
k |
(2) |
= k |
(2) |
(my , Dy ) |
статистической линеаризации |
|
|
||||
1 |
1 |
|
|
||
ипостроенные
=k1(1) (my , Dy ) и
идеального реле
приведены на рис. 5.7, б, в. Из этих графиков видно, что релейный элемент по отношению к среднему значению входного сигнала т ведет себя как линейное звено, коэффициент усиления которого k0
зависит от величины m y / 
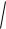 Dy .
Dy .
Таким образом, случайная составляющая входного сигнала создает эффект линеаризации нелинейного элемента для регулярной составляющей (среднего значения) сигнала. Метод статистической линеаризации формально похож на метод вибрационной линеаризации нелинейного элемента колебаниями высокой частоты постоянной амплитуды.
В свою очередь регулярная составляющая входного сигнала
128
оказывает влияние на прохождение случайной составляющей. Так, например, для рассмотренного нелинейного элемента типа идеального реле передача случайной составляющей ослабляется за счет насыщения нелинейного элемента регулярной составляющей
сигнала, поскольку коэффициенты
my .
k |
(1) |
|
|
1 |
|
и
k |
(2) |
|
|
1 |
|
уменьшаются с ростом
Ограничения в использовании метода статистической линеаризации обусловлены требованиями нормального закона распределения случайного процесса на входе нелинейного элемента, что выполняется достаточно хорошо, если линейная часть системы будет обладать свойствами низкочастотного фильтра.
Метод статистической линеаризации особенно эффективен при анализе стационарного режима работы системы автоматического управления. В этом случае my = const , Dy = const и коэффициенты
статистической линеаризации не зависят от времени. Линеаризованная система является при этом системой с постоянными параметрами и ее исследование может быть проведено сравнительно просто.
В нестационарном режиме, который может быть вызван, например, переходным процессом, нестационарностью воздействий или самой системы, коэффициенты статистической линеаризации изменяются во времени. Линеаризованная система оказывается при этом системой с переменными параметрами и ее исследование усложняется. Исследования системы в этом случае могут производиться с помощью цифровых вычислительных машин.
5.5. Расчет нелинейных систем методом статистической линеаризации
При расчете нелинейных систем ставится задача определения в стационарном режиме статистических характеристик любой координаты системы [регулируемой величины X (t) , ошибки E(t) и
др.] по известным статистическим характеристикам входного случайного сигнала. Входной сигнал G(t) в данном случае может
представлять собой либо полезный сигнал, либо линейную комбинацию полезного сигнала и помехи. При этом должны быть заданы передаточная функция линейной части системы W ( p) и
129

характеристика нелинейного элемента
.
Рассмотрим применение метода статистической линеаризации для расчета как разомкнутых, так и замкнутых систем, содержащих один безынерционный нелинейный элемент.
5.5.1. Расчет разомкнутых нелинейных систем
Структурная схема разомкнутой системы, имеющей нелинейный элемент с характеристикой и линейную часть с передаточной
функцией W ( p) , показана на рис. 5.8, а.
а
б
в
Рис. 5.8
Пусть на входе нелинейного элемента действует стационарный
случайный процесс G(t) с нормальным законом распределения |
|
||
|
|
|
|
G(t) = mg + G(t) , |
|
(5.42) |
|
где mg – математическое ожидание входного сигнала; |
|
– |
|
G(t) |
|||
центрированная составляющая случайного входного сигнала. |
|
|
|
Искомая выходная величина системы X (t) |
будет представлять |
||
собой также стационарный случайный процесс |
|
|
|
|
|
|
|
X (t) = mx + X (t). |
|
(5.43) |
|
На основе метода статистической линеаризации исходную структурную схему системы (рис. 5.8, а) можно эквивалентно заменить двумя структурными схемами: для расчета математического
130
ожидания выходной величины |
mx |
(рис. 5.8, б) и для расчета |
|
центрированной составляющей |
случайного процесса на |
выходе |
|
|
|
|
|
системы X (t) (рис. 5.8, в). |
|
|
|
Используя приведенные схемы, можно найти математическое |
|||
ожидание случайного процесса на выходе системы: |
|
||
mx = mg k0 (mg , Dg )W (0) |
(5.44) |
||
и центрированную составляющую |
случайного процесса на выходе |
|||||
системы: |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
X (t) = G(t)k1(mg , Dg )W ( p) , |
(5.45) |
||
где |
k0 (mg , Dg ) |
– эквивалентный статистический коэффициент |
||||
усиления |
нелинейного |
элемента |
по математическому |
ожиданию; |
||
k1(mg , Dg ) |
– эквивалентный статистический коэффициент усиления |
|||||
нелинейного элемента по случайной составляющей; W (0) = W ( p) | p =0
– коэффициент передачи линейной части системы. |
||
Центрированная составляющая |
|
случайного процесса на |
G(t) |
||
входе системы обычно задается своими статистическими
характеристиками: центрированной корреляционной функцией |
Rg (τ) |
|
|
|
|
или центрированной спектральной плоскостью |
S g (ω) , зная которые |
|
|
|
|
можно найти центрированную корреляционную функцию |
Rx (τ) и |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Sx (ω) |
|
|
центрированную |
спектральную |
плотность |
случайного |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
процесса на выходе системы: |
|
|
|
|
|
|
|
|
|
|
|
||||
R (τ) = k 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(m |
g |
, D |
g |
) |
|
dλ |
|
k (λ)k (η)R (τ + λ − η)dη ; |
(5.46) |
||||||
x |
1 |
|
|
|
|
|
|
|
g |
|
|
||||
|
|
|
|
|
|
|
− |
− |
|
|
|
|
|
||
|
S (ω) =| W ( jω) |2 |
[k (m |
g |
, D )]2 S (ω) , |
|
(5.47) |
|||||||||
|
x |
|
|
|
|
|
|
|
|
1 |
g |
g |
|
|
|
где k (λ) и k (η) |
– импульсная переходная функция (функция веса) |
||||||||||||||
линейной части системы; W ( jω) |
– частотная передаточная функция |
||||||||||||||
линейной части системы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсия |
Dx центрированной составляющей X (t) |
случайного |
|||||||||||||
процесса на выходе системы |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dx = Rx (0) |
= (1/ π) S x (ω)dω . |
|
(5.48) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
131
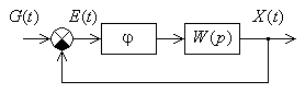
5.5.2. Расчет замкнутых нелинейных систем
Структурная схема замкнутой системы автоматического управления с одним нелинейным безынерционным элементом всегда может быть приведена к виду, показанному на рис. 5.9.
Рис. 5.9
Допустим, что входной сигнал
G(t)
, который в общем случае
может представлять собой линейную комбинацию полезного сигнала и помехи, является стационарным случайным процессом с
нормальным законом распределения |
|
|
|
|
|
G(t) = mg + G(t) . |
(5.49) |
|
В результате расчета требуется по заданным статистическим характеристикам входного сигнала определить математическое ожидание, дисперсию или другие статистические характеристики любой интересующей нас координаты системы, например ошибки E(t) , регулируемой величины X (t) и т. п.
Рассмотрим метод расчета замкнутых систем на примере определения статистических характеристик ошибки E(t) системы.
Заметим, что закон распределения случайного сигнала на выходе нелинейного элемента в общем случае отличается от нормального закона распределения, однако, проходя через линейную часть системы, обладающую в большинстве случаев свойством низкочастотного фильтра, он нормализуется и, таким образом, закон распределения выходного сигнала X (t) будет близок к нормальному.
На основе этого можно считать, что случайная ошибка E(t) на входе
нелинейного элемента также имеет нормальный закон распределения. Поэтому при расчетах можно пользоваться формулами и графиками эквивалентных статистических коэффициентов усиления k0 и k1
обычно приведенных в приложении учебников.
Ошибка системы будет представлять собой стационарный случайный процесс
132
где E(t)
|
|
|
|
|
E(t) = mε + |
E(t) , |
(5.50) |
mε |
– математическое ожидание |
(среднее значение) |
ошибки; |
– центрированная составляющая случайной ошибки.
Для простоты будем считать, что нелинейный элемент имеет
однозначную нечетную характеристику |
u = (ε) . В этом случае на |
основе метода статистической линеаризации сигнал на выходе нелинейного элемента приближенно может быть записан следующим
образом: |
|
|
|
||
|
U (t) = mu +U (t) = k0 |
(mε , Dε )mε + k1(mε , Dε )E(t) , (5.51) |
где mu – математическое ожидание сигнала на выходе нелинейного |
|
|
|
элемента; U (t) |
– центрированная составляющая случайного процесса |
на выходе нелинейного элемента; k0 (mε , Dε ) – эквивалентный статистический коэффициент усиления нелинейного элемента по
математическому ожиданию; |
k1(mε , Dε ) |
– эквивалентный |
статистический коэффициент усиления нелинейного элемента по случайной составляющей.
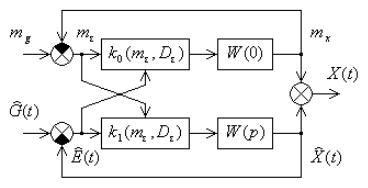
В результате статистической линеаризации нелинейный элемент эквивалентно заменяется двумя линейными безынерционными элементами: один из них с коэффициентом усиления k0 и второй – с
коэффициентом усиления k1 .
При этом исходная нелинейная замкнутая система (рис. 5.7) эквивалентно заменяется двумя замкнутыми связанными линеаризованными системами (рис. 5.10): по математическому ожиданию; по центрированной случайной составляющей.
Рис. 5.10
Передаточные функции разомкнутых линеаризованных систем
133

равны: по математическому ожиданию
Wm |
( p) = k0 (mε , Dε )W ( p) , |
ε |
|
по центрированной случайной составляющей
W ( p) = k (m , D )W ( p) . ε 0 ε ε
Передаточные функции замкнутых линеаризованных относительно ошибки равны:
по математическому ожиданию
Wm m |
( p) = |
1 |
= |
|
|
1 |
; |
||
+W |
1 + k |
(m |
, D )W ( p) |
||||||
g |
ε |
1 |
( p) |
|
|||||
|
|
|
m |
ε |
0 |
ε |
ε |
|
|
|
|
|
|
|
|
|
|
||
по центрированной случайной составляющей
(5.52)
(5.53)
систем
(5.54)
|
W |
( p) = |
|
|
1 |
|
= |
|
1 |
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
gε |
|
1 +Wmε |
( p) 1 |
+ k0 (mε , Dε )W ( p) |
|
||||
|
|
|
|
|||||||
Передаточные функции (5.52) и (5.53) взаимосвязаны |
||||||||||
коэффициенты |
k0 |
и |
1 |
, которые |
являются функциями |
|||||
|
|
|
|
k |
|
|
|
|
|
|
неизвестных величин mε |
|
и |
Dε . |
|
|
|
|
|
||
(5.55)
через
пока
Заметим, что полученные таким образом две связанные линеаризованные системы будут линейными только при
определенных постоянных значениях m |
и |
D |
т. е. при стационарном |
ε |
|
ε |
|
режиме системы. При нестационарном режиме система остается
нелинейной, так как коэффициенты |
k0 и |
1 |
зависящие от |
mε |
и |
Dε , |
|
|
|
|
k |
|
|
|
|
будут переменными. |
|
|
|
|
|
|
|
Если случайный процесс |
G(t) |
на входе системы стационарный, |
|||||
то
mg
=
const
. В этом случае математическое ожидание
mε
ошибки
связано с математическим ожиданием mg входного сигнала следующим соотношением:
m |
= W |
(0)m |
|
= |
|
|
1 |
|
g |
|
|
|
|
||||
ε |
m m |
|
1 |
+ k |
(m |
, |
D )W |
|
|
g |
ε |
|
|||||
|
|
|
0 |
ε |
|
ε |
||
|
|
|
|
|
|
Дисперсия ошибки
D = |
1 |
S |
(ω)dω = |
1 |
| W |
( jω) |2 |
||
|
|
|||||||
ε |
2π |
|
ε |
|
2π |
|
gε |
|
|
− |
|
|
− |
|
|
||
|
|
|
|
|
|
|
||
(0) mg .
Sg (ω)dω ,
(5.56)
(5.57)
где Sg (ω) – спектральная плотность центрированной случайной составляющей G(t) входного сигнала; Sε (ω) =| Wgε ( jω) |2 Sg (ω) | – спектральная плотность центрированной случайной составляющей
134

ошибки.
Уравнения (5.56) и (5.57) образуют систему алгебраических уравнений:
m |
− |
|
|
|
|
1 |
|
|
m |
|
= 0; |
|
|
|
|
|
|
|
|
|
g |
|
|
||||
ε |
|
1 + k |
(m |
, |
D )W (0) |
|
|
|
|||||
|
|
|
|
|
|
||||||||
|
|
|
0 |
|
ε |
|
|
ε |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
2 |
|
|
− |
|
| |
|
|
|
|
|
| |
|
|||
ε |
|
|
|
|
|
|
|
g |
|||||
|
|
|
|
|
|
|
|
||||||
D |
|
|
|
|
|
|
|
|
|
S |
|||
|
|
2π |
− |
1 + k |
(m |
, D )W ( j ) |
|
|
|||||
|
|
|
|
|
1 |
ε |
ε |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
(ω)dω = 0. |
|
|
|
||
|
||
|
|
(5.58)
Система уравнений
коэффициенты k0 и |
k1 |
(5.58) содержит два неизвестных |
mε |
и |
Dε |
и |
являющиеся функциями этих неизвестных.
Решая систему уравнений, можно найти математическое ожидание
mε |
и дисперсию |
Dε |
ошибки в установившемся режиме. Решение |
системы уравнений (5.58) можно произвести либо методом последовательных приближений, либо графоаналитическим методом.
При решении методом последовательных приближений
задаются вначале некоторыми значениями коэффициентов k0 и |
1 |
и |
|||
|
|
|
|
k |
|
по (5.56) и (5.57) находят m |
и |
D |
в первом приближении. По |
||
ε |
|
ε |
|
|
|
найденным значениям
mε
и
Dε
уточняют величины
k0
и k1 пользуясь
(5.37), (5.38), (5.39), (5.34) или графиками зависимостей
k |
(m |
, |
0 |
ε |
|
Dε
)
,
k |
(m |
, |
1 |
ε |
|
Dε )
. Затем весь цикл вычислений коэффициентов
k0
и |
1 |
|
k |
повторяется многократно до тех пор, пока в процессе приближений последующие значения коэффициентов не будут с достаточной точностью совпадать с предыдущими значениями.
Решение графоаналитическим методом производится обычно тогда, когда уравнения системы (5.58) имеют сложный вид. В этом случае в координатах mε и Dε строят кривые, соответствующие
обоим уравнениям системы (5.58); точка пересечения этих кривых дает решение указанной системы уравнений.
После того как будут определены математическое ожидание и дисперсия ошибки, по известным методам линейной теории можно при необходимости рассчитать математическое ожидание и дисперсию случайного сигнала в любой интересующей нас точке системы.
В заключение следует отметить, что метод статистической линеаризации может быть применен и к системам с несколькими нелинейными элементами. Если несколько нелинейных элементов
135
включены последовательно друг с другом, то они могут быть заменены одним нелинейным элементом с результирующей нелинейной характеристикой, построенной по характеристикам отдельных нелинейных элементов. После этого производят статистическую линеаризацию результирующего нелинейного элемента и методом, изложенным выше, находят математическое ожидание и дисперсию в любой интересующей нас точке системы.
Если нелинейные элементы разделены друг от друга инерционными линейными звеньями, то каждый из нелинейных элементов заменяется статистически эквивалентным линейным элементом. Поскольку для каждого линейного элемента нужно определить два статистически эквивалентных коэффициента k0 и k1
то в результате, чтобы найти все коэффициенты линейных элементов,
приходится решать систему уравнений, содержащую |
q |
уравнений, |
где q – число нелинейных элементов в системе. |
В |
результате, |
естественно, расчеты значительно усложняются.
Хотя метод статистической линеаризации и является приближенным, он нашел широкое применение при инженерных расчетах нелинейных систем автоматического управления, описываемых дифференциальными уравнениями высокого порядка. Точность метода статистической линеаризации тем выше, чем уже полоса пропускания линейной части систем и чем больше плотность вероятности на входе нелинейного элемента приближается к нормальной.
5.6.Контрольные вопросы
1.Какие законы распределения случайных величин вы знаете?
2.Какими параметрами характеризуется нормальный закон распределения?
3.Что такое математическое ожидание?
4.Какими соотношениями характеризуется дисперсия?
5.Что такое корреляционная функция?
6.Как определяется спектральная плотность?
7.Как связаны корреляционные функции на входе и на выходе линейного звена?
8.Как связаны спектральные плотности на входе и на выходе линейного звена?
136
