
воздействий
Rg
(τ)
,
R |
f |
(τ) |
|
|
и
R |
gf |
(τ) |
|
|
и корреляционными функциями
искомой координаты, например корреляционной регулируемой случайной величины X (t) , может
функцией |
Rx (τ) |
быть найдена на
основе известных соотношений. Например, если случайные процессы
G(t) |
и |
F (t) |
статистически независимы, т. е. корреляция отсутствует, |
то |
|
|
|
|
x |
|
+ |
+ |
1 |
1 |
|
g |
|
R |
(τ) = |
|
|
|
|
||||
|
|
dλ |
k |
(λ)k |
(η)R |
|
|||
|
|
|
− |
− |
|
|
|
|
|
++
+dλ k2 (λ)k2 (η)R f (τ
− −
(τ +
+λ
λ−
−
η)
η)dη +
dη ,
где ki (t) – импульсные переходные характеристики.
Зная корреляционную функцию Rx (τ) , можно определить
следующие статистические характеристики случайной регулируемой величины:
среднее значение регулируемой величины
x = |
Rx ( ) ; |
среднее значение квадрата регулируемой величины x 2 = Rx (0) ;
дисперсию регулируемой величины
Dx = Rx (0) − R( ) ;
(5.1)
(5.2)
(5.3)
среднее квадратическое отклонение регулируемой величины
σ |
x |
= |
D |
x |
|
|
|
=
R |
(0) − R( ) |
x |
|
.
(5.4)
Спектральные плотности искомых координат определяют заданным спектральным плотностям внешних воздействий S g (
по
ω) ,
S |
f |
(ω) |
|
|
и
S |
gf |
(ω) |
|
|
на основе известных соотношений. Например, если
случайные процессы G(t) и
F (t)
статистически независимы, т. е.
корреляция отсутствует, то
S |
|
(ω) =| W |
|
( jω) | |
2 |
S |
|
(ω)+ | W |
|
( jω) | |
2 |
S |
|
(ω). |
x |
gx |
|
g |
fx |
|
f |
||||||||
|
|
|
|
|
|
|
|
|
|
После того как будет определена, например, спектральная плотность Sx (ω) регулируемой величины, среднее значение квадрата
регулируемой величины может быть найдено по формуле
117

|
2 |
|
1 |
+ |
1 |
|
|
x |
= |
S x (ω)dω = |
S x (ω)dω , |
||||
|
|
||||||
|
2π |
π |
|||||
|
|
|
- |
0 |
|||
|
|
|
|
|
которая получается из
|
1 |
|
|
jωτ |
|
1 |
|
jωτ |
|
|
Rx (τ) = |
|
S x (ω)e |
dω = |
S x (ω)e |
dω |
|||||
|
|
|||||||||
2π |
|
π |
|
|||||||
|
− |
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
||||
при τ = 0.
(5.5)
При расчетах систем автоматического управления часто интересуются динамической точностью системы, которая при стационарных случайных воздействиях определяется средним значением квадрата случайной ошибки системы, равной
ε |
2 |
= lim |
1 |
|
|||
|
|
||
|
|
t → 2T |
|
+T |
2 |
|
|
ε |
(t)dt |
||
|
|||
−T |
|
|
,
(5.6)
где
ε(t)
– любая реализация случайной ошибки;
T
– интервал
наблюдения.
Среднее значение квадрата определено через спектральную
формуле, аналогичной (5.5), т. е.
случайной
плотность
ошибки может |
быть |
|
ошибки |
Sε (ω) |
по |
ε |
2 |
|
|
1 |
+ |
|
= |
Sε (ω)dω = |
||
2π |
|||
|
- |
||
|
|
1 π
Sε
0
(ω)dω
.
(5.7)
Средняя квадратическая ошибка
ε |
|
= |
ε |
2 |
ск |
|
|||
|
|
|
|
.
(5.8)
Разумеется, статистические характеристики случайной ошибки
можно определять и по корреляционной функции ошибки |
Rε (τ) , |
используя формулы, аналогичные (5.1) – (5.4), однако в практических расчетах чаще всего пользуются формулой (5.7), которая быстрее и проще приводит к цели. Входящую в (5.7) спектральную плотность
ошибки |
Sε (ω) |
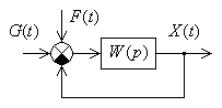
для рассматриваемой системы (рис. 5.1) при |
коррелированных полезном сигнале и помехе вычисляют по формуле
S |
(ω) =| W |
|
( jω) | |
2 |
S |
|
(ω) +W |
(− jω)W |
|
( jω)S |
|
( jω) + |
gε |
|
g |
fε |
gf |
||||||||
ε |
|
|
|
|
gε |
|
|
|
где |
S g (ω) , |
помехи; S gf
+Wgε ( jω)W fε (− jω)S fg ( jω)+ | W fε ( jω) | |
2 |
S f (ω) , |
(5.9) |
|
S f (ω) – спектральные плотности полезного сигнала и (ω), S fg (ω) – взаимные спектральные плотности между
118
полезным сигналом и помехой;
W |
gε |
( jω) =1/[1 +W ( jω)] |
|
|
– частотная
передаточная функция, связывающая ошибку |
ε(t) |
и полезный сигнал |
g (t) ; |
W fε ( jω) = W2 ( jω) /[1 +W ( jω)] |
– частотная передаточная |
функция, связывающая
1 |
|
2 |
|
– |
|
W ( jω) = W |
( jω)W |
|
( jω) |
2 |
|
разомкнутой системы; |
|
||||
|
|
|
|
W |
( |
ошибку |
ε(t) |
и |
помеху |
f (t) ; |
|
частотная |
передаточная |
функция |
|||
jω) |
– частотная |
передаточная |
функция |
||
|
|
|
|
|
|
части разомкнутой системы между точкой приложения помехи и выходом системы.
При отсутствии корреляции между полезным сигналом и помехой их взаимные спектральные плотности равны нулю и выражение для спектральной плотности ошибки упрощается:
Sε (ω) =| Wgε ( jω) | |
2 |
Sg (ω)+ | W fε ( jω) | |
2 |
S f (ω) . |
(5.10) |
||
|
|
||||||
Среднее значение квадрата ошибки системы |
ε |
2 |
в общем случае |
||||
|
|||||||
состоит из отдельных составляющих, определяемых слагаемыми
(5.9), т. е.
ε |
2 |
2 |
|
2 |
2 |
2 |
|
(5.11) |
|
= εg |
+ εgf |
+ ε fg + ε f . |
|
||||
|
|
|
2 |
для S g (ω) , |
2 |
для S f (ω) и т. д., а |
||
Обычно находят отдельно ε g |
ε f |
|||||||
затем суммируют все составляющие ошибки в соответствии с (5.11). В частном случае, когда помеха действует на входе в месте
приложения управляющего воздействия (рис. 5.4) и корреляция между полезным сигналом и помехой отсутствует, (5.10) можно записать в виде
S |
(ω) =| 1/[1 +W ( jω)] | |
2 |
S |
|
(ω)+ | W ( jω) /[1 +W ( jω)] | |
2 |
|
g |
|
||||
ε |
|
|
|
|
|
S f
(ω)
. (5.12)
Рис. 5.4
Заметим, что (5.9), (5.10) и (5.12) для спектральной плотности ошибки Sε (ω) могут быть легко переписаны для спектральной
плотности регулируемой величины Sx (ω) , если в них заменить
119
частотную передаточную функцию для ошибки |
Wgε ( jω) |
частотную передаточную функцию замкнутой системы Wgx ( jω) .
на
Чтобы найти среднее значение квадрата ошибки системы при случайных воздействиях, необходимо, зная спектральную плотность
ошибки |
Sε (ω) , вычислить интеграл (5.7). Вычисление этого |
интеграла довольно сложно, поэтому на практике его выполняют двояко: либо аналитическим методом с помощью табличных интегралов, либо методом графоаналитического интегрирования.
5.4. Статистическая линеаризация нелинейных элементов
Нелинейные элементы в общем случае вызывают искажение входного случайного сигнала. В нелинейных системах принцип суперпозиции неприменим, поэтому при одновременном воздействии на систему, например, полезного регулярного сигнала и случайной помехи из-за нелинейного преобразования этих сигналов помеха может значительно уменьшить эффект действия полезного сигнала.
Исследование нелинейных систем, находящихся под воздействием случайных процессов, значительно сложнее, чем линейных систем. Общих точных методов исследования подобных систем нет, и для изучения систем в этом случае обычно используют приближенные методы.
Наибольшее распространение в практике расчета нелинейных систем при случайных воздействиях получил приближенный метод,
называемый методом статистической линеаризации. Этот метод был разработан в 1954 г. одновременно И. Е. Казаковым в СССР и Р. Бутоном в США.
Идея метода основана на приближенной замене нелинейных преобразований процессов, происходящих в системе, статистически эквивалентными им линейными преобразованиями, при этом нелинейный элемент заменяется статистически эквивалентным линейным элементом. В результате такой замены система в целом линеаризуется и для ее исследования можно применять аппарат линейной теории.
Возможны различные критерии статистической эквивалентности, которые могут быть положены в основу метода статистической линеаризации. В тех случаях, когда линеаризуют
120
безынерционный нелинейный элемент, у которого нелинейная зависимость между входным y(t) и выходным x(t) сигналами имеет
вид |
|
|
|
|
|
x(t) = [ y(t)], |
(5.13) |
где |
|
– статическая характеристика |
нелинейного элемента, |
применяют следующие два критерия:
1.Критерий равенства математического ожидания и дисперсии случайного процесса на выходе нелинейного элемента и эквивалентного ему линейного элемента.
2.Критерий минимума математического ожидания квадрата разности случайных процессов на выходе нелинейного элемента и эквивалентного ему линейного элемента.
Познакомимся с этими критериями, ограничиваясь рассмотрением только однозначных нелинейных характеристик, которые могут быть либо нечетными, либо четными.
Напомним, что для нечетных и четных характеристик соответственно справедливы соотношения
|
|
(− y) = −( y) , |
(5.14) |
|
|
|
(− y) = ( y) . |
(5.15) |
|
Случайные процессы на входе и выходе нелинейного элемента |
||||
могут быть представлены следующим образом: |
|
|||
|
|
|
|
|
|
Y (t) = my (t) + Y (t) ; |
(5.16) |
||
|
|
|
|
|
|
X (t) = mx (t) + X (t) ; |
(5.17) |
||
где my (t) , |
mx (t) – математические ожидания входного и выходного |
|||
сигналов |
соответственно, |
включающие медленно |
меняющиеся |
|
|
|
|
|
|
регулярные составляющие; |
Y (t) , |
X (t) – центрированные случайные |
||
составляющие процессов на входе и выходе нелинейного элемента соответственно.
Заметим, что для четных нелинейных характеристик, обладающих выпрямляющими свойствами, математическое ожидание mx (t) отлично от нуля даже при my (t) = 0.
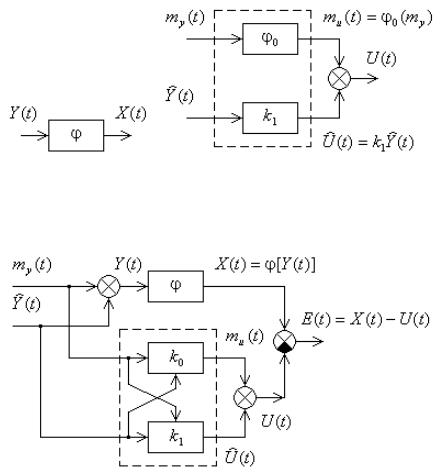
В общем случае для однозначной нелинейной функции ( y)
произвольного |
вида |
сигнал |
на |
выходе |
эквивалентного |
линеаризованного элемента |
|
|
|
||
|
|
|
|
||
|
U (t) = 0 (my ) + k1Y (t) |
= mu (t) +U (t) , |
(5.18) |
||
121
где
k1
0 |
(my ) – математическое ожидание нелинейной |
функции ( y) ; |
– |
эквивалентный статистический коэффициент |
усиления по |
случайной центрированной составляющей.
Таким образом, в общем случае нелинейный безынерционный элемент (рис. 5.5, а) заменяют двумя безынерционными элементами: нелинейным по математическому ожиданию и линейным по случайной центрированной составляющей (рис. 5.5, б).
а |
б |
Рис. 5.5
Рис. 5.6
В частном случае, когда нелинейный безынерционный элемент
имеет нечетную характеристику, функция 0 |
может быть |
представлена в виде |
|
0 = k0my (t) , |
(5.19) |
где k0 – эквивалентный статистический коэффициент усиления
нелинейного элемента по математическому ожиданию (по средней составляющей).
122

В этом случае нелинейный элемент можно эквивалентно заменить двумя линейными элементами с коэффициентами усиления
k0 |
и |
k1 |
(рис. 5.6). Численные значения этих коэффициентов при |
заданной нелинейной зависимости определяются значениями
математического ожидания и дисперсии случайного сигнала на входе нелинейного элемента.
Покажем сначала, как находят коэффициенты |
0 |
, |
k0 |
и k1 в |
случае статистической линеаризации, основанной на первом критерии статистической эквивалентности, состоящем в выполнении равенства математического ожидания и дисперсии случайного процесса на выходе нелинейного элемента и эквивалентного ему линейного элемента, т. е. когда
mx (t) = mu (t) ; |
(5.20) |
Dx (t) = Du (t) . |
(5.21) |
Принимая во внимание (5.18), получаем |
|
0 = mu (t) = mx (t) . |
(5.22) |
Для нечетных нелинейностей, учитывая (5.19), получим |
|
k0 = mx (t) / my (t) . |
(5.23) |
Чтобы найти статистически эквивалентный коэффициент
k1
перепишем (5.21) следующим образом:
D |
(t) = D |
2 |
] = M |
(t) = M [{U (t)} |
|||
x |
u |
|
|
|
2 |
] = |
|
||
[{k Y (t)} |
||
1 |
|
|
k |
2 |
D |
|
|
y |
||
1 |
|
||
(t)
,
откуда
k |
= k |
(1) |
|
||
1 |
1 |
|
= |
D |
(t) / D |
(t) |
|
x |
y |
|
=
σ |
x |
(t) / |
|
|
σ y
(t)
.
(5.24)
Обозначение k |
(1) |
показывает, что коэффициент |
k1 найден по |
||||||||
|
|
||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
первому критерию эквивалентности. |
|
|
|
|
|
|
|
|
|||
Статистические |
коэффициенты |
|
0 |
, |
k |
0 |
и |
k (1) |
можно также |
||
|
|
|
|
|
|
|
|
1 |
|
||
выразить через нелинейную зависимость и плотность вероятности w( y) случайного сигнала Y (t) на входе нелинейного элемента:
|
|
|
|
|
|
|
|
|
|
0 = mx (t) = |
( y)w( y)dy ; |
(5.25) |
|||||
|
|
|
|
|
− |
|
|
|
|
|
mx (t) |
|
|
1 |
|
|
|
k0 |
= |
= |
|
|
( y)w( y)dy ; |
(5.26) |
||
|
|
|
||||||
|
|
my (t) |
|
my ( y) − |
|
|||
123

X (t)
Знаки и U (t)
|
|
|
|
|
|
|
|
|
|
1 |
|
|
(1) |
|
1 |
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
||||||
|
= |
|
|
|
|
( y)w( y)dy − m |
(t) . |
(5.27) |
|||
1 |
|
|
x |
||||||||
k |
|
|
|
|
|
||||||
|
|
|
Dy (t) − |
|
|
|
|
|
|||
в (5.24) и (5.27) следует выбирать такими, чтобы знаки совпадали.
Второй критерий статистической эквивалентности требует выполнения условия минимума математического ожидания квадрата разности процессов на выходе нелинейного элемента и эквивалентного линейного элемента, т. е.
|
2 |
= |
|
Подставляя в (5.28)
M [{X (t) −
значения
U (t)}2 X (t)
] =
и
min U (t
.
) ,
(5.28)
определяемые по
(5.17) и (5.18),
|
2 |
|
получим
= M[{m |
(t |
x |
|
|
|
|
|
|
2 |
|
) + X (t) − |
|
(m |
|
|
] = min |
|
0 |
y |
) + k Y (t)} |
||||
|
|
1 |
|
|
||
.
После выполнения операции возведения в квадрат и вычисления математического ожидания имеем
|
2 |
2 |
(t) + D |
2 |
(m |
|
|
= m |
(t) − |
y |
|||
|
|
x |
x |
0 |
|
− 2k R |
(0) |
1 xy |
|
) + k D |
y |
(t) − 2 |
m |
x |
(t) − |
1 |
0 |
|
|
||
= min , |
|
|
|
|
|
(5.29)
где mx (t) – математическое ожидание случайного процесса на выходе |
|||||||
нелинейного элемента; |
|
2 |
] , |
|
2 |
|
– |
|
Dx (t) = M [{X (t)} |
] |
|||||
Dy (t) = M [{Y (t)} |
|
||||||
дисперсия центрированного случайного процесса на входе и выходе |
||
нелинейного элемента соответственно; |
Rxy |
|
(0) = Dxy (t) = M [ X (t)Y (t)] |
||
|
|
|
– математическое ожидание (среднее значение) произведения двух |
||||||
|
|
|
|
|
|
|
случайных функций |
X (t) и Y (t) |
, |
равное |
начальному |
значению |
|
взаимной корреляционной функции |
Rxy (0) . |
|
|
|||
|
|
|
|
|
|
|
При заданных значениях mx (t) , |
D y (t) , |
Dx (t) , Rxy (0) |
величина |
|||
|
|
|
|
|
|
|
ε 2 является функцией параметров |
0 |
и k . |
|
|
||
Значения 0 и |
1 |
|
1 |
|
|
|
при которых выполняется (5.28) найдем, если |
||||||
|
k |
|
|
|
|
|
приравняем нулю частные производные функции ε 2 по параметрам
|
0 |
и k |
. Имеем ε 2 / |
0 |
= 2 |
0 |
− 2m |
x |
(t) = 0 |
, откуда |
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 = mx (t) . |
|
(5.30) |
||
|
|
В |
случае нечетной |
нелинейной характеристики |
, учитывая |
|||||||
(5.19) получаем следующее выражение для коэффициента k0 :
124

|
|
|
|
|
|
k0 = mx (t) / my (t) . |
|
||
Значение коэффициента k1 находим из |
|
||||||||
|
ε |
2 |
/ |
k |
= 2k D |
|
(t) − 2R (0) = 0 |
||
|
|
y |
|||||||
|
|
|
|
|
1 |
1 |
xy |
|
|
откуда |
|
|
|
|
|
|
|
|
|
k1 |
= k |
(2) |
= Rxy (0) / Dy (t) = Rxy |
(0) / Ry (t) . |
|||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Обозначение |
k |
(2) |
|
показывает, что коэффициент |
|||||
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
второму критерию эквивалентности.
k1
(5.31)
(5.32)
найден по
Статистический коэффициент |
k |
(2) |
|
||
|
1 |
|
плотность вероятности w( y) входного нелинейную зависимость , т. е.
можно выразить также случайного сигнала Y
через
(t) и
|
(2) |
|
|
1 |
|
|
|
|
= |
|
|
( y |
|||
|
|
|
|
||||
1 |
|
|
|
||||
k |
|
D |
|
(t) |
|
||
|
|
|
y |
− |
|||
|
|
|
|
|
|||
−
my
) ( y)w( y)dy
,
(5.33)
где
|
|
|
|
||
( y − my ) ( y)w( y)dy = x(t) y(t) = D |
||
− |
||
Обычно значение коэффициента
|
|
= |
xy |
|
|
k |
(1) |
|
|
||
|
1 |
|
Rxy |
(0) . |
|
|
, определенное из первого
критерия по (5.24), является несколько завышенным, a |
k |
(2) |
|
||
|
1 |
|
определенное из второго критерия по (5.32), – несколько заниженным, поэтому при расчетах рекомендуется брать их среднеарифметическое значение, т. е.
1 |
= (k |
(1) |
+ k |
(2) |
) / 2 |
. |
(5.34) |
|
|
||||||
k |
|
|
|
|
|||
|
1 |
1 |
|
|
|
||
Сравнивая полученные выражения, видим, что коэффициенты0 и k0 получаются одинаковыми при статистической линеаризации
как по первому критерию, так и по второму.
Из (5.25), (5.26), (9.27) и (5.33) видно, что статистически эквивалентные коэффициенты усиления зависят не только от вида
характеристики нелинейного элемента |
( y) , но и от закона |
распределения (плотности входе нелинейного элемента
вероятности) случайного процесса на w( y) .
При использовании метода статистической линеаризации приближенно полагают, что закон распределения случайного процесса является нормальным. Такое предположение можно сделать потому, что при прохождении случайного сигнала с любым законом распределения через линейные инерционные звенья на выходе
125
последних закон распределения случайного сигнала оказывается близким к нормальному. При этом, чем инерционнее система, тем закон распределения случайного сигнала на ее выходе ближе к нормальному. Наличие нелинейного элемента в системе нарушает это, однако при достаточно узкой полосе пропускания линейной части системы имеется тенденция к восстановлению нормального закона распределения.
При нормальном законе распределения плотность вероятности однозначно определяется математическим ожиданием и дисперсией случайного процесса, поэтому в этом случае коэффициенты k0 и k1
будут лишь функциями математического ожидания my и дисперсии Dy входного сигнала, т. е.
k |
0 |
= k |
(m |
, D |
); |
|
0 |
y |
y |
|
k1
= k |
(m |
, |
1 |
y |
|
Dy
)
.
(5.35)
To обстоятельство, |
что коэффициенты |
k0 |
и |
1 |
|||
|
|
|
|
|
|
|
k |
параметров |
my |
и |
Dy |
входного сигнала, отражено |
|||
зависят от на рис. 5.6
пунктирными линиями.
Формулы (5.25), (5.26), (9.27) и (5.33) при нормальном законе распределения будут иметь вид:
|
|
|
|
|
0 |
k |
0 |
= |
|
|
|
|
|
|
|
|
1 |
|
|
= |
|
|
( y) |
|
|||
|
|
2 D |
|
||||
|
− |
|
y |
||||
|
|
|
|||||
1 |
|
|
1 |
|
|||
|
( y) |
|
|||||
m |
|
2 D |
|||||
y − |
|||||||
|
|
|
|
||||
|
−( y −m |
|
) |
2 |
|
e |
y |
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
e |
−( y −m |
y |
||
|
|
|
|
||
|
|
|
|
|
|
y |
|
|
|
|
|
/(2D |
y |
) |
||
|
|
|
|
|
) |
2 |
/(2D |
||
|
||||
dy ; |
||
y |
) |
dy |
|
||
|
|
|
;
(5.36)
(5.37)
k |
(1) |
= |
1 |
|
|||
|
|
||
1 |
|
D |
|
|
|
|
|
|
|
|
y |
k |
(2) |
= |
1 |
|
|||
|
|
||
1 |
|
D |
|
|
|
|
|
|
|
|
y |
|
|
2 |
|
1 |
|
−( y −m |
y |
) |
2 |
/(2D |
y |
) |
|
|
|
|
2 |
|
|
( y) |
e |
|
dy |
||||||||||||||
|
|
|
|
|
|
|
|
|
− m |
|
||||||||
|
|
|
|
2 Dy |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
−( y −m |
|
) |
2 |
/(2D |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
( y − my ) ( y) |
|
|
e |
y |
|
y |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
− |
|
|
|
2 D |
y |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1/ 2 |
|
|
||
|
; |
|
|
|
|
|
|
|
) |
dy . |
|
|
||
(5.38)
(5.39)
Если умножить выражение (5.37) продифференцировать произведение k0my по
на
my
my , затем и сопоставить
полученное выражение с (5.39), то можно убедиться в выполнении следующего равенства:
k (2) |
= d (k |
m |
y |
) / dm |
y |
= dm / dm |
y |
= d |
0 |
/ dm |
y |
. |
(5.40) |
||
1 |
|
0 |
|
|
|
x |
|
|
|
|
|||||
Соотношение |
(5.40) |
может |
быть |
|
использовано |
как для |
|||||||||
126
