
Сборник задач
.pdf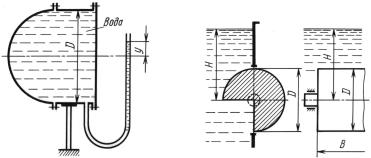
Показать в виде векторов горизонтальные и вертикальные со- |
|
ставляющие сил давления воды на днища. |
|
Ответ. Горизонтальные составляющие сил давления на правое и ле- |
|
вое днища одинаковы и равны +1,54 кН; –1,54 кН и 0; |
вертикальные соста- |
вляющие сил давления на полусферу одинаковы для трех случаев и равны |
|
2,57 кН. |
|
Задача 3.2. В прямоугольном окне вертикальной стенки резер- |
|
вуара установлен на цапфах цилиндрический затвор диаметром |
|
D = 0,8 м и длиной B = 3 м. |
|
1. Определить усилие на цапфы и момент от действия воды на |
|
затвор в изображенном на эскизе положении при напоре H = 1 м. |
|
2. Какими будут усилия на цапфы и момент, |
если повернуть за- |
твор на 180◦? |
момент от действия |
Ответ. 1. Усилие на обе цапфы P = 23,8 кН; |
|
жидкости M = 628 Н ∙ м. 2. P = 24,7 кН; M = 0. |
|
К задаче 3.1 |
К задаче 3.2 |
Задача 3.3. Показание манометра, присоединенного к днищу |
|
бака, M = 10 кПа. |
воздуха, находящегося над водой, если |
Найти давление Px |
|
Определить растягивающее Pраст и срезающее Pсрез усилия |
|
h1 = 1,8 м и h2 = 1 м. |
|
болтов, крепящих к вертикальной стенке бака коническую крышку |
|
с размерами d = 0,8 м и l = 0,6 м; массой крышки пренебречь. |
|
Найти зависимость этих сил от давления M. |
|
Ответ. Px = −17,5 кПа (разрежение); Pраст = −3,82 кН (крышка |
|
прижимается к баку давлением снаружи); Pсрез = 0,98 кН. |
|
Задачи 3.4. |
Цилиндрический затвор диаметром D = 1,2 м и |
длиной L = 16 |
м, масса которого 40 т, может открываться путем |
|
61 |
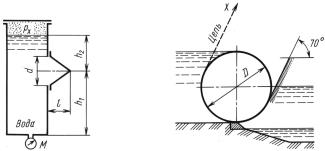
выкатывания его вверх по наклонным направляющим (α = 70◦) |
|
с помощью цепи. |
|
Определить величину и направление силы P давления воды на |
|
закрытый затвор. |
|
Найти натяжение X цепи при трогании затвора с места и при |
|
выходе его из воды. |
|
Как изменятся сила давления воды на затвор и натяжение цепи, |
|
если уровень воды за плотиной поднимется до оси затвора? |
|
Ответ. |
P = 144 кН; угол с горизонтом 38◦100; X = 123 кН при тро- |
гании и 184 |
кН при выходе из воды. |
К задаче 3.3 |
К задаче 3.4 |
Задача 3.5. Определить силу Q, прижимающую стальной (от- |
|
носительная плотность δ |
= 8) шаровой всасывающий клапан ра- |
диусом R = 100 мм к седлу, имеющему диаметр d = 125 мм, если |
|
диаметр насосного цилиндра D = 350 мм, а усилие, действующее |
|
на шток поршня, P = 4 000 Н. |
|
Седло клапана расположено ниже оси цилиндра на h1 = 0,5 м |
|
и выше свободной поверхности в резервуаре с атмосферным давле- |
|
нием на h2 = 6,5 м, причем труба под клапаном заполнена водой. |
|
Ответ. Q = 1 640 Н. |
|
Задача 3.6. Секторный затвор радиусом R = 5 м и длиной |
|
L = 4,5 м поддерживает напор воды H = 3,5 м. Для пропуска воды |
|
затвор поднимается цепью, поворачиваясь вокруг горизонтальной |
|
оси на цапфах диаметром d = 150 мм. |
|
Масса затвора равна 3 |
т, его центр тяжести расположен на бис- |
сектрисе угла сектора радиус
При закрытом затворе( ось егоr =вращения0,75 R). и верхний обрез секто ра лежат в одной горизонтальной плоскости расположенной выше- свободной поверхности на h = 1 м. ,
62

|
К задаче 3.5 |
К задаче 3.6 |
|
1. Определить силу P , действующую на подшипники закрытого |
|||
затвора. |
|
|
|
2. |
Найти силу N, прижимающую затвор к порогу. |
||
3. |
Вычислить начальное натяжение Q цепи при подъеме затвора |
||
(коэффициент трения в цапфах принять f = 0,3). |
|||
Ответ. |
1. P = 398 кН; угол с горизонтом 47◦. 2. N = 42,8 кН. |
||
3. Q = 20,5 кН. |
|
||
Задача 3.7. Секторный затвор плотины радиусом R = 4,5 м под- |
|||
держивает напор воды |
H = 3 м. |
||
Поворачиваясь вокруг оси O, затвор может погружаться в вы- |
|||
емку, |
выполненную в теле плотины и заполненную водой. |
||
Пренебрегая трением в опорах вращения, определить усилие T , |
|||
с которым затвор прижимается к уступу A плотины (приходящееся |
|||
на 1 м длины затвора), |
если масса 1 м длины затвора равна 1 т; раз- |
||
меры a = 4 |
м и b = 0,3 |
м, плечо центра тяжести затвора c = 0,6 м. |
|
Ответ. |
T = 47,1 кН. |
||
К задаче 3.7 |
К задаче 3.8 |
63
Задача 3.8. Горизонтальный цилиндрический сосуд диаметром |
||||
d = 0,8 м с полусферической и конической тонкостенными крыш- |
||||
ками заполнен жидкостью плотностью ρ1. Правая половина цилин- |
||||
дра (с конической крышкой) вставлена в замкнутый резервуар и на- |
||||
ходится под уровнем другой жидкости (плотностью ρ2) на глубине |
||||
a = 2 м. |
|
|
|
|
Определить горизонтальные Pг и вертикальные Pв составля- |
||||
ющие сил давления жидкости на полусферическую и коническую |
||||
крышки A и B, если показание вакуумметра V = 10 кПа, показание |
||||
манометра M = 30 кПа и |
ρ1 |
= ρ2 = 1 000 кг/м3. |
||
Показать в виде векторов горизонтальные и вертикальные со- |
||||
ставляющие сил давления жидкости на полусферу и конус. Как из- |
||||
менятся силы при ρ1 = 0,8ρ2 = 800 кг/м3? |
||||
Ответ. Для полусферы Pг |
= −5,03 |
кН и Pв = 1,31 кН; для конуса |
||
Pг = −30 кН и P = 0; при P |
= 0,8ρ2 |
горизонтальные составляющие |
||
не изменятся; вертикальная составляющая, |
действующая на полусферу, |
|||
Pв0 = 1,05 кН, на конус P 0 = −0,263 кН. |
|
содержащего масло отно- |
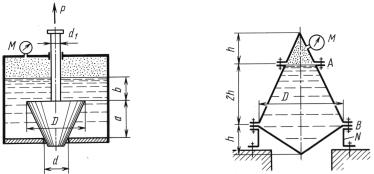
||
Задача 3.9. Отверстие в дне сосуда, |
||||
сительной плотностью δ |
= 0,83, закрыто конической пробкой с |
|||
размерами D = 100 мм, |
d = 50 мм и a = 100 мм, укрепленной |
|||
на штоке диаметром d1 = 25 |
мм. Уровень масла расположен выше |
|||
пробки (b = 50 мм). |
|
1. Определить начальное усилие P , необходимое для подъема |
|
пробки при избыточном давлении в сосуде M = 10 кПа. |
ока- |
2. Найти избыточное давление M, при котором усилие P |
|
жется равным нулю. |
|
К задаче 3.9 |
К задаче 3.10 |
64
|
|
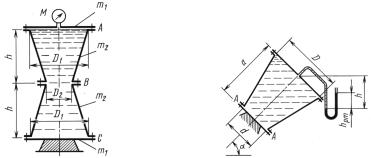
К задаче 3.11 |
|
|
|
|
|
|
К задаче 3.12 |
|
|
|
|
|||||||||||
|
Массой пробки и трением в сальнике пренебречь. |
|
|
|
|
|||||||||||||||||||
|
Ответ. |
1. P = 13,5 |
Н. |
|
2. M = 1,04 |
кПа. |
|
|
|
|
|
|
|
|
|
|||||||||
|
Задача |
3.10. Определить усилия, |
нагружающие болтовые груп- |
|||||||||||||||||||||
пы A и B сборного конического резервуара, содержащего воду, если |
||||||||||||||||||||||||
h = 1 |
м, наибольший внутренний диаметр сосуда D = 3 |
м, а пока- |
||||||||||||||||||||||
зание манометра M = 40 |
кПа. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Ответ. |
PA = 31,4 кН; Pв = 355 кН. |
нагружающие болтовые груп- |
|||||||||||||||||||||
|
Задача |
3.11. Определить усилия, |
||||||||||||||||||||||
пы A, B и C симметричного сосуда размерами D1 |
= 1,8, D2 = 0,9 |
м |
||||||||||||||||||||||
и h = 1,2 |
м; m1 = 600 |
кг и m2 = 900 кг – массы крышки и кониче- |
||||||||||||||||||||||
ской обечайки сосуда. |
Сосуд заполнен водой, |
избыточное давление |
||||||||||||||||||||||
M = 50 кПа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Как изменятся усилия, действующие на болты, если вместо ука- |
|||||||||||||||||||||||
занной на эскизе опоры подвесить сосуд за верхнюю крышку? |
кН |
|
||||||||||||||||||||||
|
Ответ |
. |
PA = 121 |
кН |
; |
PB = 7,1 |
кН |
; PC = 128 |
кН |
; |
A |
= 185 |
; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
P 0 |
|
|
||||||||||||
B |
|
|
кН |
|
C |
|
|
кН |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
P 0 |
Задача |
3.12. |
Определить растягивающее Pраст и срезающее |
|||||||||||||||||||||
= 71,5 |
|
|
|
; |
P 0 |
= 192 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Pс |
ез |
усилия, действующие на болты фланца A конического ре- |
||||||||||||||||||||||
зервуара размерами D = 1 м; d = 0,5 м и a = 1 |
м, |
заполненного |
||||||||||||||||||||||
жидкостью плотностью |
ρ = 750 кг/м3. |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Давление в резервуаре измеряется ртутным манометром, пока- |
|||||||||||||||||||||||
зание которого hрт = 300 |
мм; высота h = 0,5 |
м. |
|
|
|
|
|
|
|
|
||||||||||||||
|
Угол наклона оси резервуара к горизонту |
α = 45◦; массу резер- |
||||||||||||||||||||||
вуара не учитывают. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Ответ. |
Pраст |
= 5,76 кН; Pсрез = 2,38 кН. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
Задача |
3.13. |
Полый барабан диаметром D = 250 мм и дли- |
|||||||||||||||||||||
ной l |
= |
|
|
1 м отформован и заливается чугуном |
(относительная |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65 |
||
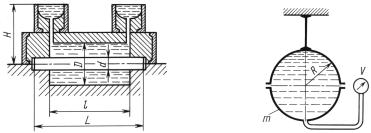
плотность δ Для получения внутреннего отверстия в фор му заложен чугцилиндрический= 7). стержень относительная плотность- δ диаметром мм и длиной ( м Уровень чугуна в литнике= 2,5) расположенd =на80высоте Н Lм=над1,2осью. формы
Определить максимальный изгибающий= 0,5 момент . дей ствующий1. на стержень при заливке формы Mизг, - Найти вертикальную силу которая.стремится поднять опо ку при2. заливке формы P , - Стержень при отливке. рассматривать как балку свободно лежа
щую на двух опорах Влиянием литников на искомую, силу прене- бречь. . -
Ответ Н м кН
Задача. 1. MизгШаровой= 33,4 сосуд∙ . 2радиусом.P = 7,12 . м заполненный водой висит3.14на. тяге прикрепленной к егоRверхней= 0,4 ,половине Ка кое наименьшее, давление, в центре сосуда показание пружинного. - вакуумметра удержит свободную нижнюю( половину сосуда мас сой кгV ) -
Ответитьm = 150 на?поставленный вопрос, принимая m = 0.
Ответ. Разрежение в центре: V1 = 5,55 кПа; V2 = 2,62 кПа.
Задача |
К задаче 3.13 |
К задаче 3.14 |
3.15. Каков наименьший уровень H воды в сосуде, при |
||
котором стальной шар (относительной плотностью δ = 8) ради- |
||
усом R = 100 мм, перекрывающий круглое отверстие диаметром |
||
d = 1,5 R в вертикальной стенке, будет находиться в равновесии? |
||
Ответ. |
H = 1,48 м. |
|
Задача |
3.16. Определить растягивающие Pраст и срезающие |
|
Pсрез усилия в болтах диаметрального фланцевого соединения ша- |
||
рового сосуда радиусом R = 0,4 |
м, заполненного наполовину водой |
|
66 |
|
|
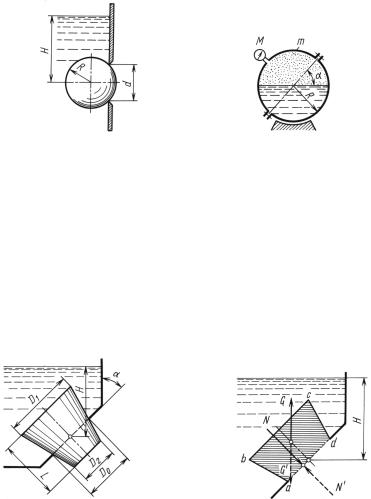
К задаче 3.15 |
К задаче 3.16 |
и находящегося под внутренним избыточным давлением сжатого |
|
газа M = 20 кПа. |
|
Плоскость стыка наклонена к горизонту под углом α = 45◦; |
|
масса полушара m = 300 кг. |
кН. |
Ответ. Pраст = 7,98 кН; Pсрез = 2,32 |
|
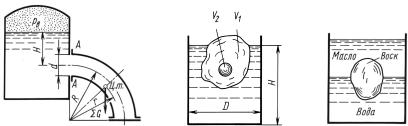
Задача 3.17. Отверстие диаметром D0 = 200 мм в плоской стен- |
|
ке, наклоненной к вертикали под углом α = 45◦, перекрыто кони- |
|
ческой пробкой, размеры которой D1 |
= 300 мм, D2 = 150 мм и |
мм Уровень воды в сосуде мм L =Определить300 . силу давления водыHна=пробку500 . .
К задаче 3.17 |
|
|
|
|
К решению задачи 3.17 |
||
Указание. Помимо общего способа нахождения сил по двум задан- |
|||||||
ным направлениям, силу давления на смоченную поверхность пробки |
|||||||
abcd можно определить при помощи следующего приема. Предположим, |
|||||||
что жидкость находится с противоположной стороны этой поверхности |
|||||||
(при таком же уровне H); тогда из условия равновесия заштрихованного |
|||||||
объема «фиктивной» жидкости найдем, что сила ее давления на рассма- |
|||||||
триваемую поверхность |
|
|
|
|
|
||
|
|
0 |
= |
|
0 + |
|
0, |
|
P |
N |
G |
||||
|
|
|
67 |
||||
где |
|
|
0 – |
сила давления на плоскую стенку ad; |
|
0 – вес заштрихованного |
||||||||||||||||
N |
G |
|||||||||||||||||||||
объема жидкости. |
|
|
|
|
||||||||||||||||||
|
|
Так как сила давления на каждый элемент поверхности определяется |
||||||||||||||||||||
глубиной его погружения под уровень жидкости, при замене действитель- |
||||||||||||||||||||||
ной жидкости «фиктивной», значение силы давления на поверхность не |
||||||||||||||||||||||
изменяется, но изменяется ее направление на противоположное. Следова- |
||||||||||||||||||||||
тельно, |
искомая сила давления |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
0 и |
|
|
|
|
P = N + G, |
|
|
|
|
||||||
|
|
|
|
= − |
|
0. |
|
|
|
|
||||||||||||
N = −N |
G |
G |
|
|
|
|
||||||||||||||||
|
|
Ответ. |
Составляющая силы P , нормальная плоскости отверстия, |
|||||||||||||||||||
P1 = 85,3 Н, |
а параллельная плоскости отверстия P2 = 68,7 Н. |
|||||||||||||||||||||
|
|
Задача 3.18. Определить отрывающее Pотр и сдвигающее Pсдв |
||||||||||||||||||||
усилия и изгибающий момент M на фланце |
A, крепящем колено |
|||||||||||||||||||||
90◦ |
|
к баку если разрежение воздуха в баке |
pв |
= 10 |
кПа и глубина |
|||||||||||||||||
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Диаметр колена d = 400 мм, радиус кривизны его оси R = 1 м |
||||||||||||||||||||
H = 1,8 м. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и масса m = 100 кг. Центр тяжести колена, |
заполненного водой, |
|||||||||||||||||||||
принять расположенным на биссектрисе в точке r = 0,9 R. |
||||||||||||||||||||||
|
|
Как влияет давление воздуха в сосуде на искомые усилия и мо- |
||||||||||||||||||||
мент? |
|
|
Pотр = 0,96 кН; Pсдв = 2,92 кН; M = 1 850 Н ∙ м. |
|||||||||||||||||||
|
|
Ответ. |
||||||||||||||||||||
|
К задаче 3.18 |
К задаче 3.19 |
К задаче 3.20 |
Задача 3.19. В цилиндрическом сосуде плавает кусок льда отно- |
|||
сительной плотностью δ1 = 0,9, в который впаян стальной шарик |
|||
относительной плотностью δ2 = 7,8. Объем льда V1 = 12 дм3, объ- |
|||
ем шарика V2 = 50 см3. |
|
|
|
1. |
Какая часть Vx объема тела находится над водой? |
||
2. |
Как изменится уровень |
H в сосуде, |
когда лед растает, если |
диаметр сосуда D = 500 мм? |
|
|
|
68 |
|
|
|
Ответить на поставленные вопросы еще для следующих двух |
||||||
вариантов задачи. |
|
|
|
|||
1. |
Вместо стального шарика объем V2 заполнен льдом. |
|||||
2. |
Объем V2 представляет воздушную полость. |
|||||
Ответ. |
1. Vx |
= 0,86 |
л. |
2. |
Уровень понизится на 1,73 мм. |
|
Задача |
3.20. |
В сосуд, |
заполненный водой и маслом (ρм = |
|||
= 900 кг/м3), погружен кусок воска (ρ = 960 кг/м3). |
||||||
Определить, какая часть объема воска погрузится в воду и какая |
||||||
останется в масле? |
|
|
|
|||
Ответ. |
В воду погрузится 0,6 объема воска. |
|||||
Задача |
3.21. 1. Прямоугольный параллелепипед относительной |
|||||
плотностью δ = 0,7 со стороной квадратного основания a = 250 мм |
||||||
и высотой b плавает в воде. |
|
|||||
Какому условию должна удовлетворять высота b, чтобы равно- |
||||||
весие плавающего параллелепипеда было устойчивым? |
||||||
2. |
В той же жидкости плавает куб со стороной a. Какому усло- |
|||||
вию должна удовлетворять относительная плотность δ материала |
||||||
куба, чтобы равновесие плавающего куба было устойчивым? |
||||||
Ответ. |
1. b ≤ 0, 222 |
м. |
2. δ не должна быть в пределах 0,211. . . 0,789 |
|||
и не может быть больше |
1, |
так как в этом случае куб потонет. |
||||
Задача |
3.22. На понтоне с размерами дна 12×4 м, высотой бор- |
|||||
та 1,2 |
м и массой 8 т перевозят котел массой 16 т, центр тяжести |
|||||
которого расположен на высоте 1 м над палубой понтона. |
||||||
1. |
Определить глубину x погружения понтона при установке ко- |
|||||
тла на его середине. |
|
|
|
|||
2. |
Найти максимальный момент Mизг, изгибающий поперечное |
|||||
сечение корпуса понтона. |
|
|||||
3. |
Подсчитать момент устойчивости Mуст при боковом крене |
|||||
θ = 10◦. |
|
|
|
|
|
|
Считать массу понтона распределенной равномерно по всему |
||||||
дну, а центр тяжести его поперечных сечений расположенным на |
||||||
0,8 м ниже палубы. |
2. Mизг = 235 кН ∙ м. 3. Mуст = 51 кН ∙ м. |
|||||
Ответ. |
1. x = 0,5 м. |
|||||
Задача |
3.23. |
Бензин (относительная плотность δ = 0,7) под из- |
||||
быточным давлением p = 30 кПа подводится к поплавковой камере |
|
карбюратора по трубке диаметром d = 4 мм. |
|
Шаровой поплавок массой 25 г и игла массой 12 г, перекрываю- |
|
щая доступ бензина, укреплены на рычаге (a = 40 мм, b = 15 |
мм), |
который может поворачиваться вокруг неподвижной оси O. |
|
|
69 |
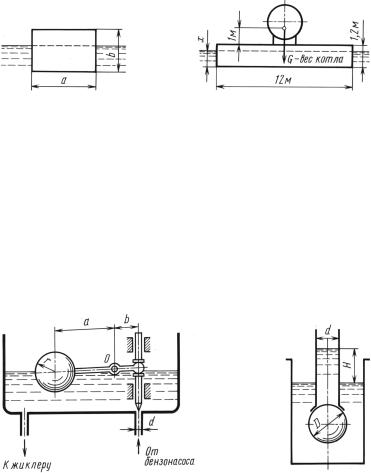
К задаче 3.21 |
К задаче 3.22 |
Определить радиус r поплавка из условия, что в момент откры- |
|
тия отверстия поплавок был погружен наполовину. Трением в шар- |
|
нирах и массой рычага пренебречь. |
|
Ответ. r = 28,8 |
мм. |
Задача 3.24. Погруженный в воду полый шаровой клапан диа- |
|
метром D = 150 мм и массой m = 0,5 кг закрывает выходное |
|
отверстие внутренней трубы диаметром d = 100 мм. |
|
При какой разности уровней H клапан начнет пропускать воду |
|
из внутренней трубы в резервуар? |
|
Ответ. H = 161 |
мм. |
К задаче 3.23 К задаче 3.24
Задача Подводный железобетонный туннель круглого сечения с внутренним3.25. диаметром м и толщиной стенки δ мм удерживается от всплыванияD = тросами3 расположен ными= 250попарно через каждые м длины туннеля T , - Определить натяжение тросов6 принимая что. дополнительная нагрузка приходящаяся на м длины, туннеля, кН а плот ность бетона, 2,5 т/м3. 1 , G = 10 , -
Ответ. 75,5 кН на один трос.
70
