Сборник задач

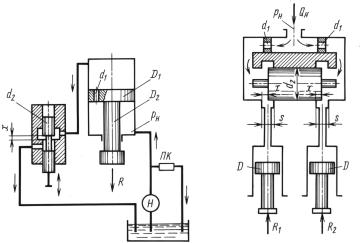
К задаче 7.48

К задачам 7.49 и 7.50

Для синхронизации работы гидроцилиндров использован дели-

тель расхода (порционер), в котором две ветви потока проходят че-

рез дроссельные шайбы диаметром d1 = 2 мм и цилиндрические

золотниковые окна высотой s = 2 мм, перекрываемые плавающим

поршеньком диаметром d2 = 10 мм.

При неодинаковых нагрузках гидроцилиндров поршенек сме-

щается в сторону менее нагруженной ветви, изменяя сопротивле-

ния ветвей (за счет неодинаковых открытий золотниковых окон) и

поддерживая равенство расходов, поступающих в гидроцилиндры.

Определить скорость vп

установившегося движения поршней

гидроцилиндров, давление p

насоса на входе в делитель и смеще-

ние х поршенька из крайнего левого положения при нагрузках ги-

дроцилиндров R1 = 20 000 Н и R2 = 15 000 Н.

Коэффициент расхода дроссельных шайб принять μ = 0,6 и зо-

лотниковых окон μ2 = 0,5.

Потерями напора в трубах, трением и утечками в гидроцилин-

драх пренебречь.

Ответ. vп = 6,1 см/с; pн = 12 МПа; х = 1,9 мм.

Задача 7.50. В делителе расхода по схеме задачи 7.49 нагрузки

гидроцилиндров равны R1 = 25 000 Н и R2 = 20 000 Н.

Определить скорость vп

установившегося движения поршней,

если известно, что давление на входе в делитель pн = 20 МПа, а

плотность жидкости ρ = 850

кг/м3.

191

Каким будет при этом смещение х плавающего поршенька в де-

лителе?

Ответ. vп = 12,5 см/с; x = 1,8 мм.

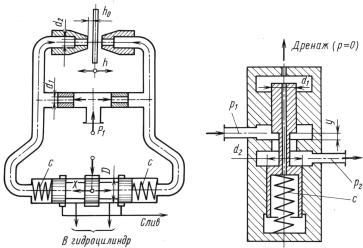
Задача 7.51. В двухсопловом гидроусилителе заслонка переме-

щена в сторону одного из сопл на величину h от среднего поло-

жения h0, чем вызван перепад давления

p

на торцах распредели-

тельного золотника и, как следствие этого,

его перемещение

от

нейтрального положения. Считая, что силы давления на торцах зо-

лотника уравновешиваются только пружинами, определить х, если

давление питания гидроусилителя p1 = 6 ∙ 106 Па и перемещение

заслонки h = 0,5h0.

Жесткость каждой из пружин золотника c = 130 Н/мм, его диа-

метр D = 10 мм.

Расход через сопло определять по формуле

Q = μ2 πd2(h0 − h)s

,

2ρ

p

где μ2 – коэффициент расхода сопла; р –

давление перед соплом;

ρ – плотность жидкости.

К задаче 7.51

К задаче 7.52

Задачу решить для случая, когда πd2h0 =

πd12

и μ1 = μ2, где

μ1 – коэффициент расхода входного дроссельного отверстия и d1 –

его диаметр.

4

2c p1 = 0, 9 мм, где n = h0 .

Ответ. x = 4 + n4

n

πD2

h

Задача 7.52. Для понижения давления на некотором участке ги-

дросистемы применяют редукционный клапан, в котором требуе-

мая разница давлений создается за счет потерь напора в клапанной

щели. В показанной на рисунке конструкции задано давление на

входе 1 = 20 МПа и давление на выходе 5 МПа.

Пренебрегая трением, определить диаметр клапана d1 и его

подъем у, если диаметр дифференциального поршня d2 = 15 мм

и расход жидкости через клапан

Q = 6,3

л/с. Жесткость пружины

c = 20,2 Н/мм и ее натяг при у

= 0 L0

= 5 мм. Коэффициент

расхода клапана μ = 0,6. Плотность жидкости ρ = 900 кг/м3.

Указание. Силу давления на клапан определять по формуле

π

P =

d22 − d12 p2.

4

Ответ. d1 = 12 мм; у = 1 мм.

Задача 7.53. Для понижения давления на некотором участке ги-

дросистемы применен редукционный клапан, схема которого пока-

зана на рисунке.

что сила давления на клапан

Пренебрегая трением и считая,

определяется выражением Р =

p2

πd2

, определить редуцирован-

ное давление p2, которое будет иметь место при расходе через кла-

4

пан Q = 0,6 л/с, если давление на входе в клапан p1 = 10 МПа.

Вычислить для этого случая подъем

у клапана, приняв его коэффи-

циент расхода μ = 0,6.

Как изменится расход через клапан и его подъем, если редуци-

рованное давление изменится до p2 = 7 МПа при том же давле-

нии p1?

= 235 Н/мм, ее сжатие l = 2 мм. Диаметр

Жесткость пружины

клапана d = 10 мм. Плотность жидкости ρ = 900 кг/м3.

Ответ. р2 = 6 МПа; у

= 0,4 мм.

При р2 = 7 МПа у = 0,1 мм и

Q = 0,27 л/с.

193

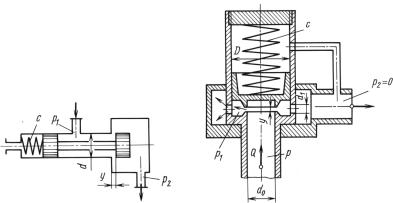
К задаче 7.53

К задаче 7.54

Задача 7.54. Для защиты гидросистемы от недопустимого по-

вышения давления применяют предохранительный клапан.

Открытие клапана и перепуск жидкости в линию слива проис-

ходит в тот момент, когда сила давления жидкости на клапан ста-

новится равной силе натяжения пружины, прижимающей клапан к

седлу.

Особенность показанной на рисунке конструкции состоит в том,

что при открытом клапане поток жидкости в нем проходит после-

довательно через два сопротивления

– клапанную щель (d0, у) и

дроссельные отверстия (d1), благодаря чему в промежуточной меж-

ду этими сопротивлениями камере создается некоторое избыточное

давление p1, которое дает дополнительное усилие сжатия клапан-

ной пружины.

Определить внешний диаметр клапана D, если требуется, что-

бы при расходе через клапан Q = 2 л/с давление

в подводящем

патрубке перед клапаном было равно давлению открытия клапана

p = p0 = 2, 5 МПа. Определить при этом подъем клапана у. Диа-

метр подвода 15 мм.

принять равным коэффици-

Коэффициент расхода клапана μ0

енту расхода дроссельного отверстия

μ1: μ0 = μ1

= 0,6. Число

отверстий i = 4, диаметр каждого d1

= 4,5 мм. Жесткость пружи-

ны c = 600 Н/мм.

Плотность жидкости ρ = 900 кг/м3.

Ответ. D = 30

мм; у = 1,0 м.

194

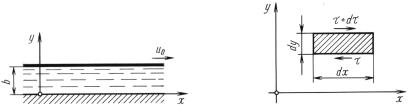
Рис. 8.1

Рис. 8.2

трения τBdx и (τ + dτ)Вdx, поэтому уравнение равномерного дви-

жения имеет вид

−τBdx + (τ + dτ)Bdx = 0,

откуда

dτ = 0 или τ = C,

где C – постоянная.

Воспользуемся теперь законом жидкостного трения Ньютона,

согласно которому касательное напряжение, возникающее в слое

жидкости, пропорционально угловой скорости деформации сдвига

элементов этого слоя. Для равномерного плоскопараллельного дви-

жения закон Ньютона имеет вид

τ = ±μ

du

(8.1)

,

dy

где μ – динамическая вязкость; u – скорость движения слоя.

В рассматриваемом случае при выбранном направлении осей

координат следует взять знак плюс (du > 0 при dy > 0),

поэтому

первый интеграл уравнения движения имеет вид

μ

du

= C.

dy

Интегрируя вторично, получаем

C

u =

y + C1.

Постоянные C и C1

μ

найдем из условий на границах потока:

u = 0 при у = 0; u = u0

при у = b.

196

u0y

(8.2)

u =

.

b

T = τF = μ

u0

F.

(8.3)

Расход жидкости через поперечноеbсечение зазора шириной B

b

Q = Z0 uBdy =

u

0

Bb.

(8.4)

2

Очевидно, что средняя скорость такого фрикционного течения

равна половине скорости движения пластинки, т. е. v = u0/2.

При выводе предполагалось, что температура в слое неизменна

и, следовательно, вязкость жидкости постоянна.

Приведенные рассуждения позволяют вычислить момент тре-

ния на вращающемся с постоянной угловой скоростью

валу

Рис. 8.3

Рис. 8.4

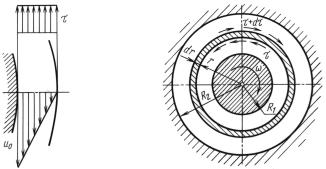
При малом относительном зазоре кривизной слоя жидкости

можно пренебречь, рассматривая движение жидкости в зазоре как

плоскопараллельное. Эпюры скоростей и касательных напряже-

ний будут тогда такими, как показано на рис. 8.5,

и момент трения

(формула Н.П. Петрова)

μ0

M = τπDL

D

=

μ

πD2L,

(8.5)

2

2b

где u0 – окружная скорость вала; L –

длина подшипника.

Заметим, что фрикционное движение жидкости в зазоре между

валом и подшипником имеет ламинарный характер для чисел Рей-

нольдса, определяемых неравенством Re ≤ 30r b , если вращает-

D

ся вал, а подшипник неподвижен. В случае же вращения наружного

цилиндра при неподвижном внутреннем ламинарное движение со-

храняется в области чисел Рейнольдса Re ≤ 2 000, причем число

Рейнольдса определяется как

Re =

u0Dг

=

u0

2b

.

v

v

Рис. 8.5

Рис. 8.6

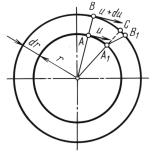
Выделим кольцевой бесконечно малый элемент жидкости, раз-

мер которого в радиальном направлении равен

dr, а по образую-

щей – l (рис. 8.6).

Поскольку движение жидкости в зазоре является фрикционным,

внешними силами, приложенными к выделенному кольцу, являют-

ся только касательные силы трения: τ ∙ 2πrl на его внутренней по-

верхности и (τ + dτ)2π(r + dr)l – на наружной.

Составляя уравнение моментов сил трения относительно оси

вращения, получаем

τ ∙ 2πrlr − (τ + dτ)2π(r + dr)l(r + dr) = 0.

После несложных преобразований и исключения членов более

высокого порядка малости последнее уравнение приводится к виду

где A – постоянная. d(τr2) = 0, или τr2 = A,

(8.6)

Рассматриваемое плоское движение

является криволинейным, поэтому вы-

ражение закона Ньютона (8.1) для жид-

костного трения здесь неприменимо.

Получим выражение закона Ньютона

для этого случая движения. Выделим во

вращающейся жидкости два слоя на ра-

диусах r и r + dr (рис. 8.7) и опреде-

лим скорость сдвига одного слоя отно-

сительно другого. За некоторый проме-

Рис. 8.7

жуток времени t точка

A внутреннего

слоя переместится в A1

, а точка В, которую примем для простоты

рассуждений лежащей на продолжении радиуса точки A, переме-

стится в В1.

Если скорость внутреннего слоя жидкости принять равной u и

скорость наружного слоя u+du, то очевидно дуга AA1 = ut, а дуга

Следовательно, сдвиг наружного слоя относительно внутрен-

BB1 = (u + du)t.

него

r + dr

dr

CB1 = BB1 − BC = (u + du) t − u

t =

du − u

t,

r

r

а скорость сдвига

199