
Сборник задач
.pdf
Отношение приближенного и точного выражений моментов
MП |
|
1 |
" |
R1 |
|
R1 |
2 |
# . |
|
= |
+ |
|
|||||||
M |
2 |
R2 |
R2 |
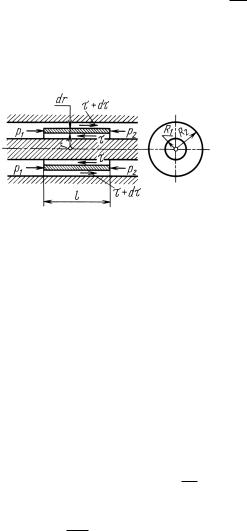
Рассмотрим напорное ламинарное движение жидкости в трубе |
||||||||||
круглого поперечного сечения, вызываемое перепадом давлений по |
||||||||||
длине трубы. |
|
|
|
|
|
|
|
|
|
|
Выделив объем жидкости в виде горизонтального цилиндра, со- |
||||||||||
осного с трубой (рис. 8.8), и составив уравнение равновесия прило- |
||||||||||
женных к нему сил, приходим к следующему дифференциальному |
||||||||||
уравнению: |
−μ |
∂u |
|
p r |
||||||
|
|
|
= |
|
|
|
|
, |
||
|
dr |
l |
2 |
|||||||
где r – радиус выделенного цилиндра; u – скорость жидкости на |
||||||||||
этом радиусе; |
– перепад давлений на длине трубы l, р = p1 − 2. |
|||||||||
Интегрируядифференциальное уравнение, получаем закон рас- |
||||||||||
пределения скоростей по сечению трубы: |
||||||||||
|
|
p |
|
|
|
|
|
|||
|
u = |
|
C |
− r2 . |
||||||
|
4μl |
|||||||||
|
|
|
Рис. 8.8 |
|
|
|||||
Определяя постоянную C из граничного условия, что скорость |
||||||||||
частиц жидкости на стенке равна нулю, находим |
|
|
||||||||
u = |
p |
R2 − r2 |
|
= umax 1 − |
r2 |
, |
(8.11) |
|||
4μl |
|
R2 |
||||||||
где R – радиус трубы. |
|
|
|
|
|
|
|
|||
Скорости распределяются в поперечном сечении трубы по пара- |
||||||||||
болическому закону, максимум скорости имеет место на оси трубы: |
||||||||||
|
|
|
|
|
|
p |
|
|
||
|
|
|
umax = |
|
|
R2. |
|
|
||
|
|
|
|
4μl |
|
|
||||
|
|
|
|
|
|
|
|
|
|
201 |

Средняя скорость v равна половине максимальной скорости:
|
umax |
|
pR2 |
|
v = |
|
= |
|
. |
2 |
8μl |
|||
Заменяя в этом выражении R через D и р через hп ρg, где hп – потеря напора и ρ – плотность жидкости2, получаем
|
|
|
|
|
gρD2 |
|
|
|
|
|
||||||||||
|
|
|
v = |
|
|
|
|
|
|
|
|
hп. |
|
|
||||||
|
32μl |
|
|
|||||||||||||||||
|
|
Решая это уравнение относительно hп, находим выражение по- |
||||||||||||||||||
терь напора при ламинарном течении в трубе: |
|
|
||||||||||||||||||
|
|
|
hп = 32 |
|
|
μl |
v. |
|
|
|||||||||||
|
|
|
ρgD2 |
|
|
|||||||||||||||
|
|
Так как μ = νρ, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
hп = 32 |
|
νl |
|
|
|
(8.12) |
|||||||||||
|
|
|
|
|
|
|
v. |
|||||||||||||
|
gD2 |
|||||||||||||||||||
|
|
Формулу (8.12) можно привести к виду |
|
|
||||||||||||||||
|
|
|
h = λ |
l |
|
|
v2 |
, |
|
(8.13) |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
п |
|
|
|
D 2g |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где λ – коэффициент сопротивления трения (λ = |
64 |
, здесь Re = |
||||||||||||||||||
|
||||||||||||||||||||
|
vD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Расход жидкости через поперечное сечение трубы (формула Пу- |
||||||||||||||||||
азейля) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
πD2 |
|
πg D4 |
|
|
||||||||||||
|
|
|
Q = v |
|
|
= |
|
|
|
hп. |
(8.14) |
|||||||||
|
|
|
4 |
|
128 |
νl |
||||||||||||||
|
|
Следует заметить, что полученные выше зависимости, справед- |
||||||||||||||||||
ливые для стабилизированного ламинарного течения непримени мы для входного участка трубы где происходит формирование, ла- минарного потока Длина входного, начального участка ламинарно-
. -
202
го течения зависит от диаметра трубы и числа Рейнольдса и опре деляется выражением -
Lнач ≈ 0,03ReD.
Для приближенного вычисления потерь на начальном участке можно пользоваться формулой (8.13), принимая λ = 70 .
Более сложным случаем ламинарного движения являетсяRe осе вое течение жидкости под действием перепада давлений в кольце- вом зазоре образованном двумя соосно расположенными цилин- дрическими, поверхностями (рис. 8.9). -
Рис
Чтобы найти закон распределения. 8.9 скоростей по сечению зазо ра выделим бесконечно малый кольцевой элемент рассмотрим дей- ствующие, на него силы и составим уравнение его, движения: -
(p1 − p2)2πrdr − τ2πrl + (τ + dτ)2π(r + dr)l = 0.
Обозначая и пренебрегая членом π τ имею щим более высокийp1 − pпорядок2 = p малости по сравнению2 сldостальнымиdr, - членами после несложных преобразований получаем следующее дифференциальное, уравнение:
prdr + ld(τr) = 0,
интегрируя которое (с учетом того, что τ = μdudr ), находим
pr2
u = −4μl + C1 ln r + C2.
203

Постоянные С1 и С2 находятся из граничных условий при |
||||||||||||||||||||||||
r = R2, u = 0 |
и при r = R1, u = 0. |
Закон распределения скоростей |
||||||||||||||||||||||
по поперечному сечению кольцевого зазора будет следующим: |
||||||||||||||||||||||||
|
u = |
p |
R2 |
r2 + |
|
R22 − R12 |
|
ln |
r |
. |
(8.15) |
|||||||||||||
|
4μl |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 − |
|
|
|
ln |
R2 |
|
|
R2 |
|
|
||||||||||
|
|
|
|
|
|
|
R1 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Произведя далее интегрирование скорости по сечению зазора, |
||||||||||||||||||||||||
получим выражение для расхода жидкости |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Z |
|
∙ |
|
|
|
8μl |
|
2 − |
1 |
|
|
ln R1 |
|
|
|
|||||||||
R2 |
|
|
|
|
πp |
|
R4 |
|
|
|
R22 − R12 |
|
2 |
. |
|
|||||||||
Q = |
u |
|
2πrdr = |
|
R4 + |
|
|
(8.16) |
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
R1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При R1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0 выражение (8.16) переходит в формулу Пуазейля |
||||||||||||||||||||||||
для труб круглого поперечного сечения: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
πR4p Q = 8μ2l .
При решении задачи о плоском ламинарном течении в зазоре между неподвижными параллельными пластинками (рис. 8.10) из
рассмотрения равномерного движения выделенного элемента жид кости приходим к следующему дифференциальному уравнению: -
−μdudy = pl y,
где перепад давления на длине зазора Интегралp = p1 − pэтого2 – уравнения с учетом граничного условияl.
ства нулю скорости на стенках) дает
|
pb2 |
1 − |
y2 |
, |
u = |
|
4 |
||
8μl |
b2 |
где b – зазор между пластинками.
(равен-
(8.17)
204
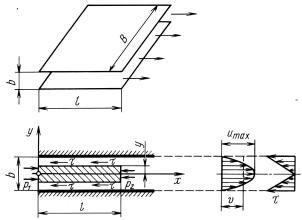
Рис. 8.10
Закон распределения скоростей по высоте зазора параболиче ский (в пространстве – параболический цилиндр), средняя– скорость-
|
|
|
|
v = 3umax, |
или v = 12 |
μlb2. |
|||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
p |
||
|
Из последней формулы легко получить выражение для расхода |
||||||||||||||||||||
жидкости в зазоре между пластинками |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
Q = |
1 |
|
|
|
p |
b3B |
(8.18) |
||||||||
|
|
|
|
|
|
|
|
||||||||||||||
и для потери напора |
|
|
12 μl |
|
|
|
|
|
|
|
|
||||||||||
hп |
|
|
|
|
νl |
|
Q |
|
|
|
|
||||||||||
|
|
|
|
|
|
= 12 |
|
, |
(8.19) |
||||||||||||
|
|
|
|
|
|
3 |
|
||||||||||||||
где |
B – ширина зазора. |
|
|
|
|
|
gb |
|
|
B |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Формулу (8.19) можно привести к виду |
|
|||||||||||||||||||
|
|
|
|
|
|
h |
= λ |
l |
|
v2 |
, |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
п |
|
|
|
Dг |
2g |
|
|
|
|
|
|||||
где |
λ = Re |
Re = |
ν г ; |
|
|
гидравлический диаметр |
|||||||||||||||
|
Dг |
|
|
– |
|
||||||||||||||||
|
|
96 |
|
|
|
vD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Dг = 2b).
205
|
|
|
|
|
|
|
Рис. 8.11 |
|
|
|
|
|
|
|
||||||
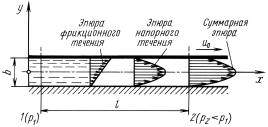
Если одна из пластинок перемещается параллельно другой с по- |
||||||||||||||||||||
стоянной скоростью u0, |
то течение жидкости в зазоре будет более |
|||||||||||||||||||
сложным, представляя собой сумму двух течений: |
фрикционного, |
|||||||||||||||||||
наведенного перемещением верхней пластинки, и напорного, вы- |
||||||||||||||||||||
званного перепадом давлений p = p1 |
− p2. Следовательно, эпю- |
|||||||||||||||||||
ра скоростей представляет сумму отдельных эпюр составляющих |
||||||||||||||||||||
движений и имеет вид, показанный на рис. 8.11. |
Ее уравнение (при |
|||||||||||||||||||
расположении начала координат в середине зазора) |
|
|||||||||||||||||||
|
u |
|
|
u |
|
|
|
y2 |
|
|
|
|||||||||
u = |
0 |
y + |
|
0 |
|
+ umax 1 − |
4 |
|
, |
(8.20) |
||||||||||
b |
|
2 |
b2 |
|||||||||||||||||
где umax – максимальная скорость напорного течения на оси зазора. |
||||||||||||||||||||
Имея функцию u = f(y), можно легко подсчитать расход через |
||||||||||||||||||||
поперечное сечение зазора и силу трения на пластинке. |
||||||||||||||||||||
При перемещении пластинки со скоростью – |
u0, т. е. в противо- |
|||||||||||||||||||
положном направлении |
(рис. 8.12), |
закон изменения скоростей по |
||||||||||||||||||
сечению зазора будет иметь вид |
|
1 − |
|
|
|
. |
|
|||||||||||||
|
|
|
y |
|
u |
|
y2 |
|
||||||||||||
u = −u0 |
|
− |
|
0 |
+ umax |
4 |
|
(8.21) |
||||||||||||
b |
2 |
|
b2 |
|
||||||||||||||||
Полученным решением можно воспользоваться для определе- |
||||||||||||||||||||
ния утечек в зазоре между поршнем и цилиндром, если только зазор |
||||||||||||||||||||
b мал по сравнению с диаметром D и если поршень расположен в |
||||||||||||||||||||
цилиндре соосно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
после подстановки |
||||
При неподвижном поршне по формуле (8.18) |
||||||||||||||||||||
B = πD имеем |
|
|
|
|
|
|
|
1 πb3D |
|
|
|
|
|
|
|
|||||
|
|
|
Q = |
|
p, |
|
|
(8.22) |
||||||||||||
|
|
|
12 |
|
|
μl |
|
|
||||||||||||
206 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
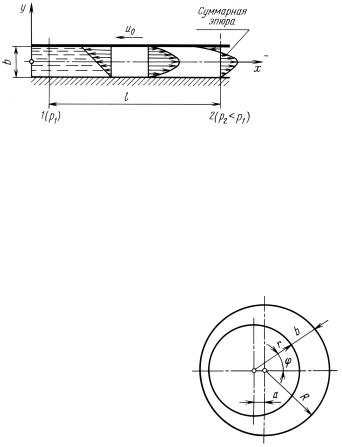
Рис. 8.12
а при движущемся с постоянной скоростью ±u0
|
|
|
|
|
|
|
1 |
|
πDb3 |
|
1 |
u0 πDb, |
|
|
(8.23) |
||||||
|
|
|
Q = |
|
|
|
|
|
|
|
p ± |
|
|
|
|||||||
12 |
|
μl |
|
|
2 |
|
|
||||||||||||||
где знак второго слагаемого зависит от направления движения |
|||||||||||||||||||||
поршня. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если поршень расположен в ци- |
|
|
|
|
|||||||||||||||||
линдре с некоторым эксцентриситетом |
|
|
|
|
|||||||||||||||||
(рис. 8.13), то зазор b |
между ними будет |
|
|
|
|
||||||||||||||||
величиной переменной в зависимости от |
|
|
|
|
|||||||||||||||||
угла ϕ, причем при малом зазоре |
|
|
|
|
|
|
|
|
|
||||||||||||
b = R + a cos ϕ − r = b0(1 + ε cos ϕ), |
|
|
|
|
|||||||||||||||||
где b0 = R − r; ε = b0 |
– |
эксцентриситет. |
|
|
|
|
|||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассматривая |
приближенно каждый |
|
|
Рис. 8.13 |
|
||||||||||||||||
элемент зазора, отвечающий прираще- |
|
|
|
||||||||||||||||||
нию угла dϕ, как плоский зазор, |
получаем следующее значение эле- |
||||||||||||||||||||
ментарного расхода: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
b3p |
|
|
|
|
b3r |
|
|
|
|
|
|
|
||||||
|
dQ = |
|
|
rdϕ |
= |
|
|
0 |
p(1 + |
ε cos ϕ)3dϕ. |
|
||||||||||
|
|
12μl |
|
||||||||||||||||||
|
|
|
12μl |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Интегрируя последнее выражение по всей окружности, находим |
|||||||||||||||||||||
расход в зазоре |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
b03rp |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
2 |
|
|||
Q = |
|
Z0 (1 + |
ε cos ϕ) |
|
dϕ = Q0 |
1 + |
|
ε , |
(8.24) |
||||||||||||
12μl |
|
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
207 |
где Q0 = 12μl |
|
– расход в зазоре при соосном расположении |
|
поршня в |
πDb03p |
||
цилиндре |
. |
||
Из полученной формулы для Q следует, что при максимальном |
|||
эксцентриситете, |
т. е. при ε = 1, |
||
|
|
|
Q = 2,5Q0. |
Заметим что при турбулентном режиме расход при наибольшем эксцентриситете, возрастает приблизительно в раза по сравне нию с расходом при концентричном кольцевом зазоре1,2 - Рассмотрим течение в клиновом зазоре вызванное. перемеще нием горизонтальной плоскости относительно, поверхности не- подвижного башмака который расположен по отношению к этой-
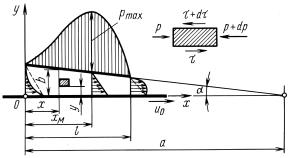
плоскости под небольшим, углом (рис. 8.14).
Рис. 8.14
Такой случай имеет место в подшипниках и подпятниках сколь жения и поэтому рассматриваемая ниже задача разъясняет суще- ство процесса, происходящего в смазочном слое - Пусть угол, клина равен α и нижняя плоскость. движется вправо
с постоянной скоростью u .
Определим расход жидкости0 в зазоре и закон распределения да вления вдоль клина предполагая поток плоскопараллельным -
Связывая оси координат, с неподвижным башмаком и распола.
гая начало координат на уровне нижней движущейся плоскости- выделим в зазоре бесконечно малый элемент жидкости и составим, уравнение его движения. Пренебрегая силами инерции по сравне-
208

нию с силами давления и трения, получаем
−dτdx − dpdy = 0, или dydτ = −dxdp .
приПоскольку при заданном направлении осей координат (du < 0 dy > 0)
|
τ = −μ |
du |
|
|||
получим |
|
, |
||||
dy |
||||||
dp |
d2u |
|
||||
|
|
|||||
|
|
= μ |
|
|
|
. |
|
|
|
|
|
||
Дважды интегрируя последнее выражение, находим |
||||||
|
dx |
dy2 |
|
|||
|
|
|
dp y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
= μu + C1y + C2. |
||||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
dx 2 |
|
|
|
|
|
|
|
и C2 используем следующие |
|||||||||||
|
|
Для определения постоянных C1 |
||||||||||||||||||||
граничные условия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
u = u0 при y = 0; u = 0 при y = b. |
||||||||||||||||||||
|
|
В итоге получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
u = u 1 |
|
y |
|
|
|
|
dp |
|
by − y2 |
. |
|
|
||||||||
− b |
|
|
|
|
||||||||||||||||||
|
|
|
|
0 |
− dx |
2μ |
||||||||||||||||
|
|
Расход жидкости в зазоре (на единицу его ширины) |
||||||||||||||||||||
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q = Z0 udy = |
|
u0b |
− |
dp |
|
b3 |
||||||||||||||
|
|
|
|
|
|
|
|
. |
|
|
||||||||||||
2 |
|
dx |
12μ |
|||||||||||||||||||
|
|
Из последнего выражения следует, что расход жидкости че- |
||||||||||||||||||||
рез поперечное сечение клина представляет сумму фрикционно- |
||||||||||||||||||||||
го расхода и расхода, обусловленного градиентом давления |
dp |
|
||||||||||||||||||||
dx |
||||||||||||||||||||||
вдоль оси х. При некотором значении координаты x = xм градиент |
||||||||||||||||||||||
|
dp |
= 0, и эпюра скоростей в этом сечении клина будет линейной. |
||||||||||||||||||||
|
|
|||||||||||||||||||||
dx |
|
|
> 0 и суммарный расход жидкости |
|||||||||||||||||||
Для всех координат x < xм |
dp |
|||||||||||||||||||||
|
||||||||||||||||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
209 |
|||||
равен разности расходов фрикционного и напорного течения; этому |
|||||||||||||
случаю соответствует левая эпюра скоростей. |
|
|
|||||||||||
Для всех координат x > xм |
|
|
|
|
dp |
< 0 и суммарный расход будет |
|||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
||
равен сумме составляющих расходов; эпюра скоростей в попереч- |
|||||||||||||
ном сечении клина показана на рис. 8.14 справа. |
|||||||||||||
Полагая далее b = ( −х) tg α ≈ (a−x)α, |
получим следующий |
||||||||||||
закон распределения давления |
по длине башмака: |
||||||||||||
|
p = |
|
6μu0x(l − x) |
. |
(8.25) |
||||||||
|
|
(2a − l)(a − x2)a2 |
|
|
|
||||||||
Кривая распределения давлении показана рис. 8.14. Исследуя |
|||||||||||||
полученную функцию p = f(x) на экстремум, находим, что макси- |
|||||||||||||
мум давления имеет место при |
|
|
|
|
|
||||||||
|
|
|
xм = |
|
a |
l |
|
|
|
||||
и равен |
|
2a |
− l |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3μu0 |
|
l2 |
|
|
|
||||||
|
pmax = |
|
|
|
|
. |
|||||||
|
|
2a2 |
|
|
(2a − l)(a − l)a |
||||||||
|
|
|
|
|
|
|
|
Зная закон распределения давле- |
|||||
|
|
|
|
ния, |
можно вычислить подъемную |
||||||||
|
|
|
|
силу на башмаке и координату цен- |
|||||||||
|
|
|
|
тра давления. |
|
|
|
||||||
|
|
|
|
|
|
|
|
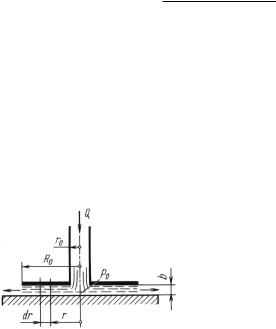
Случай течения между парал- |
|||||
|
|
|
|
лельными пластинками можно при- |
|||||||||
|
|
|
|
ближенно распространить и на зада- |
|||||||||
Рис |
. 8.15 |
|
|
чу о радиальном течении в торцевом |
|||||||||
|
|
|
зазоре, образованном двумя плоски- |
||||||||||
ми дисками (рис. 8.15). Определим расход жидкости в зазоре, если |
|||||||||||||
последний равен b, а избыточное давление подводимой жидкости |
|||||||||||||
на внутреннем радиусе r0 |
|
равно p0. |
|
|
|
|
|||||||
Применяя для кольцевого элемента бесконечно малой радиаль ной длины выведенное ранее уравнение течения между парал- лельными пластинкамиdr учитывая осевую симметрию течения и- пренебрегая силами инерции, по сравнению с силами давления и
210
