
Сборник задач
.pdf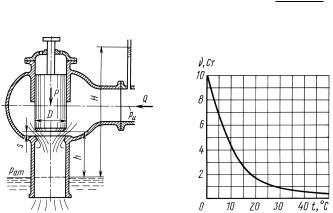
|
|
|
|
P + ρgV |
|
ρv2D2 |
||
|
|
|
|
|
= |
|
, |
|
|
|
|
|
Pм + ρмgVм |
ρмvм2Dм2 |
|||
где V/Vм = D3/Dм3. |
|
|
= 7 м/с; 3) горизонталь- |
|||||
Ответ. |
1) hп = 3,2 м; P = 90 Н; 2) v |
|||||||
ная сила |
(лобовое сопротивление) P = 400 Н; |
вертикальная (архимедова) |
||||||
P = 310 |
Н, суммарная P = 505 Н. |
|
|
|
|
|||
Задача |
5.16. |
Модель холостого выпуска гидротурбины с разме- |
||||||
ром клапана D |
= 0,2 м испытана на воздухе (ρ = 1,25 кг/м3) под |
|||||||
избыточным давлением pи = 400 |
мм вод. ст. При полном открытии |
|||||||
клапана s |
= 100 мм получен расход Qм = 1,6 м3/с; при открытии |
|||||||
sм = 20 мм получена максимальная сила действия потока на кла- |
||||||||
пан (возникающая за счет динамического разрежения на его торце) |
||||||||
Для натурного холостого выпуска диаметром D = 0,5 м, рабо- |
||||||||
Pм = 50 Н. |
|
|
|
|
|
|
|
|
тающего на воде под статическим напором H = 32 м определить |
|
(считая, что испытания модели произведены в квадратичной зоне |
|
сопротивления): |
|
1) |
расход Q при полном открытии клапана; |
2) |
максимальную силу P , действующую на клапан, если высота |
его расположения над уровнем воды м
Указание При определении силы hследует= 3 .учитывать что помимо динамического. разрежения на торце клапанаP в натуре возникает, ,статиче ское разрежение ρgh, обусловленное, весомостью жидкости и приводящее- к появлению дополнительной статической силы Pст = ρghπD2 .
Ответ. 1) Q = 3,16 м3/с; 2) P = 30,8 кН. 4
К задаче 5.16 |
К задаче 5.17 |
121

суммарный расход охлаждающей воды |
Q = 8 л/с проходит по 250 |
||||
параллельным трубкам, между которыми движется конденсируе- |
|||||
мый пар. |
|
|
|
|
|
Каков максимальный допустимый диаметр трубок, при котором |
|||||
в них еще будет турбулентное движение (обеспечивающее лучшую |
|||||
теплопередачу, чем ламинарное)? |
|
||||
Для нижней границы турбулентного режима принять Reкр = |
|||||
= 3 000. Температура воды t = 10 ◦C (ν = 0, 013 Ст). |
|||||
Ответ. dmax |
= 10 |
мм. |
|
|
|
Задача 5.19. |
В трубопроводе диаметром d и длиной l под ста- |
||||
тическим напором H |
движется жидкость, кинематическая вязкость |
||||
которой ν. Получить выражение для критического напора, при ко- |
|||||
тором ламинарный режим переходит в турбулентный, учитывая в |
|||||
трубопроводе только потери на трение. |
|
||||
Указание. Воспользоваться формулой для потерь на трение при лами- |
|||||
нарном режиме: |
|
|
H = 32νl |
v |
, |
|
|
|
gd2 |
||
|
|
|
|
|
|
имея в виду, что критический напор Hкр соответствует критической ско- |
|||||
рости vкр . |
|
3 |
кр . |
|
|
Ответ. Hкр = |
|
||||
|
32ν2lRe |
|
|
|
|
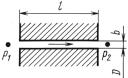
Задача Машинное масло для которого задана зависимость кинематической5.17. вязкости ν от температуры, прокачивается по тру бе диаметром мм в количестве , л с - Определитьd =режим20 движения при Q = 4 ◦/С. и ◦С и ука зать температуру соответствующую критическомуt = 10 tзначению= 40 числа-
Рейнольдса ,
Ответ (Reкр =С2 300ламинарный). С турбулентный
. t = 10 ◦ – ; t = 40 ◦ – ; tкр = = 25Задача◦C. 5.18. В поверхностном конденсаторе паровой турбины
Задача Установитьgd режим течения нефти ν Ст по трубопроводу5.20длиной. м который при располагаемом( = 2,5 ста) тическом напоре l =м1должен000 , пропускать расход л -
Найти минимальноеH = 40значение ν при котором в трубопроводеQ = 60 /c. будет еще ламинарный режим принявmin,
Указание Воспользовавшись, формуламиReкрдля= потери2 000. напора при ла минарном режиме. -
Q H = 128νl πgd4
122
и для числа Рейнольдса |
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
Re = 4 |
|
|
, |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
πdν |
|
не содержащее диа- |
|||||||||||||
найти выражение критического напора через расход, |
||||||||||||||||||||||
метра трубы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Hкр = π |
3 |
ν |
5 Reкр4 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||
Ответ. Hкр = 113 м – |
|
|
2gQ3 |
|
= 2 Ст. |
|||||||||||||||||
|
режим ламинарный; νmin |
|||||||||||||||||||||
Задача |
5.21. |
Для квадратной трубки, сторона которой a = 10 мм, |
||||||||||||||||||||
определить критическую скорость движения воды при t = 20◦С |
||||||||||||||||||||||
(ν = |
0, 01 Ст), |
воздуха при |
|
p |
|
= |
|
0,1 МПа и |
t = |
20◦С (μ = |
||||||||||||
= 1,82 ∙ 10−4 П, |
ρ = 1,17 кг/м3) |
и турбинного масла при t = 20◦С |
||||||||||||||||||||
(ν = 1 Ст), |
приняв Reкр |
= 2 000. |
воздуха – 3,1 |
м/с, масла – 20 м/c. |
||||||||||||||||||
Ответ. |
Скорость воды 0,2 м/с, |
|||||||||||||||||||||
Задача 5.22. Для узкой кольцевой щели |
|
|
|
|||||||||||||||||||
диаметром D = 250 |
мм и шириной b = 1 мм |
|
|
|
||||||||||||||||||
определить минимальный расход воды тем- |
|
|
|
|||||||||||||||||||
пературой |
10◦С |
(ν = 0, 013 Cт), при кото- |
|
|
|
|||||||||||||||||
ром сохраняется турбулентный режим; при- |
К задачам 5.22 и 5.23 |
|||||||||||||||||||||
нять в качестве нижней границы этого режи- |
||||||||||||||||||||||
ма Rекр = 3 000. |
|
|
|
|
b на значение критического расхода |
|||||||||||||||||
Будет ли влиять ширина |
||||||||||||||||||||||
(при сохранении условия, что |
|
D 1)? |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
Ответ. Qкр = 1,5 л/с независимо |
от величины b. |
|
|
|||||||||||||||||||
Задача |
5.23. |
Определить в общем виде для узкой кольцевой ще- |
||||||||||||||||||||
ли диаметром D, шириной b |
и длиной l критический перепад да- |
|||||||||||||||||||||
влений |
p = p1 |
− p2 |
, соответствующий смене режимов движения |
|||||||||||||||||||
жидкости с заданными характеристиками (плотность |
ρ, вязкость |
|||||||||||||||||||||
μ). Подсчитать |
pкр |
в частном случае (D = 250 мм, |
b = 0,5 мм, |
|||||||||||||||||||
l = 100 |
мм) для воды |
(ν = 0,01 Cт), приняв Reкр = 3 000. |
||||||||||||||||||||
Указание. Принимать, что перепад |
|
p целиком поглощается сопро- |
||||||||||||||||||||
тивлением трения: |
|
|
|
p = 12μl |
v |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
, |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
где v – средняя скорость в щели. |
|
|
|
|
|
|
|
b2 |
|
|
|
|||||||||||
Ответ. |
pкр |
= |
|
b3 |
|
Reкр; |
|
pкр = 14, 5 кПа. |
|
|
||||||||||||
|
|
|
6 |
ρν2l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
123 |

|
Глава 6. |
ИСТЕЧЕНИЕ ЖИДКОСТИ |
|
|||||
|
|
|
ЧЕРЕЗ ОТВЕРСТИЯ, |
|
||||
|
|
|
НАСАДКИ И ВОДОСЛИВЫ |
|
||||
|
ВВЕДЕНИЕ |
|
||||||
|
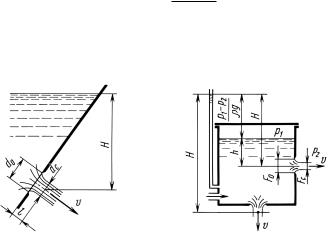
При установившемся истечении жидкости из большого откры- |
|||||||
того резервуара через круглое отверстие, размер которого мал по |
||||||||
сравнению с его заглублением под уровнем жидкости (малое отвер- |
||||||||
стие, рис 6.1), |
средняя скорость в сжатом сечении струи равна по |
|||||||
уравнению Бернулли |
|
|||||||
|
|
|
v = ϕp |
|
|
|
(6.1) |
|
где |
H – |
|
2gH, |
|||||
|
глубина центра тяжести сжатого сечения струи под уровнем |
|||||||
(напор истечения)1. Безразмерный коэффициент скорости |
|
|||||||
|
|
|
1 |
|
|
|
||
|
|
|
ϕ = p |
|
, |
(6.2) |
||
|
|
|
α + ζ |
|||||
где α коэффициент кинетической энергии в сжатом сечении струи –ζ коэффициент сопротивления отверстия выражающий потерю; напора– при истечении в долях скоростного, напора струи подсчитанного по средней скорости , В общем случае истечения из замкнутого. резервуара в газо образную среду рис напор истечения представляет раз- ность значений гидростатического( . 6.2) напора в резервуареH и в центре-
сжатого сечения струи:
1 Так как сжатое сечение находится на расстоянии от плоскости отверстия напор истечения для малого отверстия l ≈можноd0/2 приближенно относить к, его центру. (d0 H)
124
|
H = h + |
p1 − p2 |
, |
(6.3) |
|
|
ρg |
|
|
где h – глубина центра сжатого сечения струи под уровнем жидко- |
||||
сти; p1 – |
давление в резервуаре над жидкостью; p2 – |
давление среды, |
||
в которую вытекает струя; ρ – плотность жидкости.
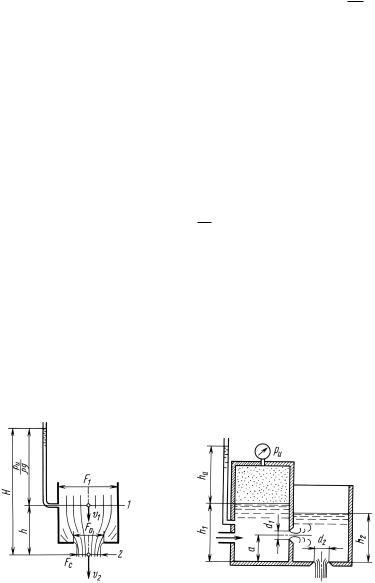
Рис. 6.1 |
|
|
|
|
|
|
Рис. 6.2 |
|
|||
Если истечение происходит в атмосферу, напор истечения пред- |
|||||||||||
ставляет глубину расположения центра сжатого сечения струи под |
|||||||||||
пьезометрическим уровнем (уровнем атмосферного давления) в ре- |
|||||||||||
зервуаре: |
h + pи |
|
|
|
|
||||||
H = |
, |
|
|
(6.4) |
|||||||
ρg |
|
|
|||||||||
|
|
|
|
|
|
|
|||||
где ри = р1 − pат – избыточное давление в резервуаре над жидко- |
|||||||||||
стью. |
|
|
|
|
|
|
|
|
|||
Степень сжатия струя, вытекающей через отверстие, характери- |
|||||||||||
зуется коэффициентом сжатия |
|
|
|
|
|
|
|
|
|||
|
Fc |
|
dc |
|
2 |
|
|||||
ε = |
= |
, |
(6.5) |
||||||||
Fо |
|
dо |
|
||||||||
где Fс, dc – площадь и диаметр сжатого сечения струи; Fo, do – |
пло- |
||||||||||
щадь и диаметр отверстия. |
|
|
|
|
|
|
|
|
|||
Расход через отверстие |
|
|
|
|
|
|
|
|
|||
Q = μFоp |
|
|
(6.6) |
||||||||
2gH, |
|||||||||||
где μ – коэффициент расхода, |
|
|
|
|
|
|
|
|
|||
|
μ = εϕ. |
|
|
|
(6.7) |
||||||
|
|
|
|
|
|
|
|
|
|
125 |
|

Значения коэффициентов истечения ϕ ε и μ круглого малого отверстия зависят от формы его кромок условий, подтока жидкости к отверстию и числа Рейнольдса, определяемого, как
|
|
|
|
|
dо√ |
|
|
|
|
|
||
|
|
Re = |
2gH |
, |
(6.8) |
|||||||
|
|
|
ν |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
где ν – кинематическая вязкость жидкости1. |
|
|||||||||||
Зависимость коэффициентов истечения от Rе для малого круг- |
||||||||||||
лого отверстия с острой кромкой дана в обработке А.Д. Альтшуля |
||||||||||||
на рис. 6.3. |
Значения μ в функции Rе приведены ниже: |
|
||||||||||
Re . . . . . . . . . 1, 5 ∙ 104 2, 5 ∙ 104 |
|
|
5 ∙ 104 |
|
|
105 2, 5 ∙ 105 5 ∙ 105 106 |
||||||
μ . . . . . . . . . . |
0,638 |
0,623 |
|
|
0,610 |
|
0,603 0,597 |
0,594 0,593 |
||||
При Rе |
≥ 105 |
число Рейнольдса практически не влияет на ко- |
||||||||||
эффициенты истечения (квадратичная зона истечения), |
и для расче- |
|||||||||||
тов можно пользоваться следующими их средними значениями: |
||||||||||||
|
ϕ = 0,97; |
ε = 0,62; |
μ = 0,60. |
|
||||||||
При этом неравномерность скоростей в сжатом сечении струи |
||||||||||||
весьма невелика и можно принимать α ≈ 1. Тогда |
|
|||||||||||
|
|
ϕ = |
|
1 |
|
, |
|
|
(6.9) |
|||
|
|
|
|
|
|
|
||||||
|
|
p |
|
|
|
|||||||
|
|
1 + ζ |
|
|
|
|||||||
откуда в среднем для круглого отверстия с острой кромкой ζ ≈ 0,06. |
||||||
Коэффициент полезного |
действия |
отверстия |
– |
отношение |
||
удельной кинетической энергии струи к напору истечения: |
||||||
η = α |
v2 |
= αϕ2 = |
α |
. |
|
|
2gH |
α + ζ |
|
|
|||
|
|
|
|
|
||
1 |
Коэффициенты истечения |
отверстий малых абсолютных размеров зависят |
||
также от числа Вебера, выражающего влияние поверхностного натяжения жидко- |
||||
сти: |
|
|
ρgHd |
|
|
We = |
о |
, |
|
|
σ |
|||
где σ поверхностное натяжение на границе струи с газообразной средой Н м При– влияние поверхностного натяжения практически отсутствует, / зо.
на автомодельностиWe ≥ 200 по We). ( -
126
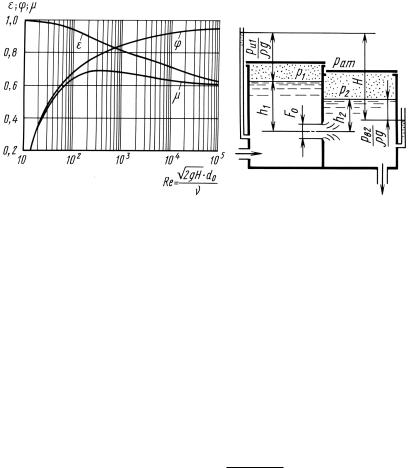
Рис. 6.3 |
|
Рис. 6.4 |
||
При больших значениях Rе можно пользоваться выражением |
||||
1 |
|
ϕ2. |
|
|
η ≈ |
|
= |
(6.10) |
|
1 + ζ |
||||
Для малых отверстий других форм при больших Rе значения |
||||
коэффициента расхода в формуле (6.6) |
можно принимать равными |
|||
При истечении под уровень (рис. 6.4) скорость жидкости в сжа- |
||||
μ = 0,6. |
|
|
||
том сечении струи и расход определяются по формулам (6.1) и (6.6), |
|||||||
в которых напор истечения H представляет разность гидростатиче- |
|||||||
ских напоров (выражаемую разностью пьезометрических уровней) |
|||||||
в резервуарах: |
|
|
|
|
pи1 − pи2 |
|
|
H = h |
1 − |
h |
2 |
+ |
. |
(6.11) |
|
|
|
|
ρg |
|
|||
Значения коэффициентов истечения для затопленного отвер- |
|||||||
стия можно принимать такими же, как при истечении свобод- |
|||||||
ной струи в атмосферу При истечении через затопленное отвер стие расход не зависит. от глубины расположения отверстия под- уровнями
Приведенные. выше значения коэффициентов истечения отно сятся к так называемому совершенному сжатию струи когда бо- ковые стенки резервуара значительно удалены от отверстия, на- расстоянии более трех линейных размеров отверстия и не влияют( на формирование струи. При расположении боковых стенок) вблизи
127
отверстия их направляющее действие уменьшает степень сжатия |
||||||||||||||||||||||||||||||
струи; при этом коэффициенты сжатия струи и расхода возрастают. |
||||||||||||||||||||||||||||||
При истечении из цилиндрического резервуара площадью F1 |
||||||||||||||||||||||||||||||
через круглое отверстие площадью F0, расположенное на его оси |
||||||||||||||||||||||||||||||
(рис. 6.5), среднее значение коэффициента сжатия струи при боль- |
||||||||||||||||||||||||||||||
ших значениях Rе можно определять по эмпирической формуле |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F0 |
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
ε = 0,62 + 0,38 |
. |
(6.12) |
||||||||||||||||||||||||
|
|
|
|
F1 |
||||||||||||||||||||||||||
Скорость истечения и расход жидкости при истечении из резер- |
||||||||||||||||||||||||||||||
вуара ограниченной площади (рис. 6.5) определяются с помощью |
||||||||||||||||||||||||||||||
уравнений Бернулли и расхода, |
записанных для сечения в резерву- |
|||||||||||||||||||||||||||||
аре перед отверстием |
(сечение |
1) |
и сжатого сечения струи (сече- |
|||||||||||||||||||||||||||
ние 2): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z1 + |
p1 |
|
+ α1 |
v12 |
|
= z2 |
+ |
p2 |
+ α2 |
v22 |
+ hп; |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
ρg |
|
|
2g |
|
|
|
|
ρg |
|
|
|
|
2g |
|
|||||||||||||||
Q = v1F1 |
= v2 εF0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Выражая потерю напора как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
hп = |
ζv22 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2g |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
и вводя напор истечения H, представляющий разность гидростати- |
||||||||||||||||||||||||||||||
ческих напоров в сечениях 1 |
и 2: |
− z2 + ρg , |
|
|||||||||||||||||||||||||||
H = |
z1 + ρg |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
p1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
||||||
получим скорость истечения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
sα2 + ζ − α1 |
F1 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
v2 = |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
p2gH |
(6.13) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
εF0 |
|
2 |
||||||||||||||
и расход |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sα2 + ζ − α1 |
F1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Q = |
|
|
|
|
|
|
|
εF0 |
|
|
|
|
|
|
p2gH. |
(6.14) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
εF0 |
|
2 |
||||||||||||||||
128 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В квадратичной зоне истечения можно приближенно принимать |
|
значения коэффициента кинетической энергии α1 = α2 = 1 |
и ко- |
эффициента сопротивления отверстия ζ = 0,06. |
=0 |
Для предельного случая неограниченного резервуара F1 |
|
F0 |
|
формулы и переходят в приведенные выше формулы и (6.13) (6.14)
(6.1)Расход(6.6)через. большое отверстие вертикальный размер которого одного порядка с напором истечения, определяется по общей фор муле в которой напор истечения, отнесенный к высоте- расположения(6.6), центра тяжестиH – отверстия при, истечении в атмосфе ру из открытого резервуара к глубине (центра тяжести отверстия- под свободной поверхностью–
На коэффициент расхода ).большого отверстия помимо факто ров, указанных для малого отверстияμ , влияет также, число Фруда -
Fr = Hh ,
где вертикальный размер отверстия
Дляh – больших отверстий с острой кромкой. коэффициент расхо да в квадратичной области истечения изменяется при разных - в пределах μ При процесс истеченияH/hста новится практически= 0,60 .автомодельным. . 0,65. Fr относительно≥ 10 числа Фруда -
В качестве примера расчета процесса истечения рассмотрим. схему на рис в которой жидкость плотностью ρ нагнетаемая в бак перетекает. 6.6,из его левой замкнутой секции в открытую, правую секцию, через отверстие диаметром d1 (расположенное в боковой
Рис. 6.5 Рис. 6.6
129

стенке на высоте и вытекает затем в атмосферу через донное от верстие диаметромa) - Определим для установившегосяd2. режима системы расход из
бака и высоту уровня в правой секции считая известными высоQ ту уровня иhпоказание2 манометра в, левой секции -
Исходнымh1 для решения задачи являетсяpи условие равенства. рас ходов через боковое и донное отверстия, при установившемся режи- ме т е при постоянных уровнях жидкости Для выбора расчетных- зависимостей( . . необходимо предварительно)выяснить. условия исте чения жидкости через боковое отверстие Для этого предположим- что h2 = a, тогда расход через боковое отверстие. ,
πd2 p и
Q1 = μ1 41 2g(h + h1 − a),
где hи = |
ри |
– высота пьезометрического уровня в левой секции. |
||||||||||||||||
|
||||||||||||||||||
|
ρg |
|
|
|
|
|
|
|||||||||||
Расход через донное отверстие |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
d2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Q2 = μ2 |
π 2 |
p2ga. |
|
|
|
|
|
|
|||||
|
|
4 |
|
|
|
|
|
|
||||||||||
Если окажется, что Q1 > Q2, то в действительности h2 > a и |
||||||||||||||||||
боковое отверстие затоплено; если Q1 < Q2, |
то h2 < а и боковое |
|||||||||||||||||
отверстие не затоплено. |
|
|
|
|
|
|
||||||||||||
В первом случае условие равенства расходов дает систему урав- |
||||||||||||||||||
нений |
|
|
|
|
|
|
||||||||||||
|
|
|
d2 |
|
|
|
|
d2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||
Q = μ1 |
π 1 |
p2g (hи + h1 − h2) = μ2 |
π 2 |
p2gh2, |
||||||||||||||
4 |
4 |
|||||||||||||||||
из которой определяются уровень h2 и расход Q. |
||||||||||||||||||
Во втором случае |
|
|
|
|
|
|
||||||||||||
|
|
|
d2 |
|
|
d2 |
|
|
||||||||||
π p и π p
Q = μ1 41 2 (h + h1 − a) = μ2 42 2gh2.
При истечении жидкости из больших резервуаров через насад ки короткие трубки различной формы рис скорость истечения- на (выходе из насадка и расход определяются, . 6.7)по формулам и (6.6). В формуле (6.6) F0 заменяется выходной площадью насадка(6.7)
130
