
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
5.6 ] Поперечные волны в струне 501
Уравнение движения (второй закон Ньютона) для куска струны , масса которого равна 39 , имеет (в проекции на ось )
вид |
|
24 |
|
|
|
|
|
|
39 |
|
|
|
, |
||
|
|
|
|
||||
|
|
2 ;9 # # |
|
||||
|
|
|
|
|
|
||
где # |
— угол между направлением касательной к струне |
||||||
в точке |
и осью : # |
. Полагая (для малых от- |
|||||
клонений), что # # |
, получаем 3 2@ 2 |
||||||
; |
|
. Разделив обе части последнего |
|||||
равенства на и перейдя к пределу при 0, получаем |
|||||||
волновое уравнение |
|
|
24 |
% 24 |
|
||
|
|
|
|
|
(5.41) |
||
|
|
|
|
|
2 - 2 |
||
|
|
|
|
|
|
||
Согласно (5.41) скорость распространения упругих волн в струне
|
- |
|
(5.42) |
% |
|
|
|
Возможными решениями уравнения являются волны вида |
|
||
@ , , |
(5.43) |
||
бегущие слева направо (знак « » в (5.43)) и справа налево (знак « » в (5.43)), а также их суперпозиция — стоячая волна
@ ,
Понятно, что мы имеем дело с поперечными волнами, поскольку, согласно (5.43), волны распространяются вдоль оси , а смещения частиц струны происходит в направлении , т. е. перпендикулярно направлению распространения (напомним, что в случае стержня речь шла о продольных волнах). Волновое
число в (5.43) есть: 3 ; Рассуждения, которые мы провели, исследуя продольные
упругие волны в стержне, закрепленном на концах, полностью применимы к натянутой струне. В частности, возможные типы колебаний описываются теми же формулами: возможны лишь такие стоячие волны, для которых на струне укладывается целое
число полуволн:
+ 2
Соответствующие частоты колебаний
|
- |
или ( |
-% |
|
|
% |
2 |
|
|
Возможные типы стоячих волн определяются формулой |
||||
@ , |
(5.44) |
|||
|
|
|
|
|
502 |
Упругие волны |
[ Гл. 5 |
5.7. Общие выводы
Мы рассмотрели несколько физических систем, в которых возбуждаются упругие волны: продольные упругие волны в твердых телах, жидкостях и газах, а также поперечные волны в натянутой струне. Во всех случаях мы пришли к выводу, что возникшее в среде возмущение распространяется в виде волны, т. е. удовлетворяет одному и тому же уравнению (4.4), в ко-
тором константа , имеющая смысл скорости распространения волны, определяется физическими параметрами невозмущенной системы: модулем упругости - и плотностью в случае твер-
дого тела, величиной в равновесном состоянии в случае газов, натяжением при равновесии ; и плотностью в случае поперечных колебаний струны. Этот результат обусловлен тем,
что при выводе волнового уравнения мы каждый раз делали
предположение о малости возмущений: исследуя продольные волны в стержне, мы предполагали, что справедлив закон Гука —
линейная связь между напряжением ; и величиной деформации < — закон, справедливый лишь при малых деформациях. При
изучении волн в газах мы полагали, что имеет место линейная связь между изменением давления и изменением плотности газа, а это справедливо лишь при малых изменениях давления (малых в сравнении с давлением в газе в стационарных условиях). При выводе волнового уравнения для натянутой струны мы также предположили, что струна мало отклоняется от положения равновесия, поэтому неизменным (и равным стационарному значению) остается величина натяжения струны при колебаниях.
Именно благодаря предположению о малости возникающих возмущений, мы каждый раз приходили к линейному уравне-
нию, для которого справедлив принцип суперпозиции: если в системе возможны волны 91 , и 92 , , то возможна и волна
вида
9 , 191 , 292 , ,
где 1 и 2 — произвольные постоянные. Другими словами, если 91 и 92 есть решения уравнения (4.4), то и функция 9 , , являющаяся линейной комбинацией решений 91 и 92, также есть решение. В частности, мы выяснили, что стоячие волны A , , описываемые соотношением (5.26), являются собственными типами продольных упругих волн (модами) для стержня длины +, закрепленного на концах. Следовательно, в таком стержне возможно и волновое возмущение вида
A , A , |
(5.45) |
при произволных постоянных Ясно, что, во-первых, функ-

5.7 ] Общие выводы 503
ция (5.45) является решением волнового уравнения (5.4) и, вовторых, подчиняется граничным условиям на концах
A , 0 при 0 и +
Последнее очевидно, поскольку каждое слагаемое в (5.45) обращается в нуль на закрепленных концах стержня.
Более того, как доказывают математики, любая возможная волна в стержне с закрепленными концами может быть представлена (при правильном подборе коэффициентов ) линейной суперпозицией собственных типов волн, т. е. в виде (5.45). Конкретный вид волны, т. е. конкретный набор коэффициентов зависит от начальных условий — от способа создания волнового возмущения.
Уравнение, описывающее волновой процесс, перестает быть линейным, если возмущение не является малым: изменение давления при распространении волны в газе не мало по сравнению со стационарным значением 80; деформация твердого тела при распространении упругой волны велика настолько, что закон Гука нарушается; отклонение струны при колебаниях столь велико, что натяжение изменяется. При этом нарушается принцип суперпозиции. Физически это связано с тем, что волна большой амплитуды изменяет свойства среды, в которой она распространяется. В конечном счете это приводит к тому, что параметр, входящий в волновое уравнение, уже не определяется только характеристиками невозмущенной среды, он начинает зависеть от амплитуды волны, если амплитуда не мала. Ясно, что волновое уравнение (4.4), в котором есть функция возмущения 99 ), нелинейно, что и приводит к нарушению принципа суперпозиции.
Одно из проявлений нелинейности — изменение формы волнового возмущения по мере распространения волны. Дело в том,
что при звуковых возмущениях волно- |
|
|
вые поверхности, соответствующие местам |
à |
|
сильных (нелинейных) сжатий упругой сре- |
|
|
|
||
ды, бегут с б´ольшей скоростью, чем по- |
á |
|
верхности, в которых среда разрежена, т. е. |
||
|
||
горбы деформаций бегут быстрее «впадин», |
|
|
|
||
что и приводит к изменению формы волны, |
â |
|
к увеличению крутизны волновых фронтов, |
|
|
отвечающих участкам сильных сжатий. |
|
|
|
||
Первоначально синусоидальная упругая |
|
|
волна большой амплитуды (рис. 5.9 а) ста- |
Рис. 5.9 |
|
новится по мере распространения в среде |
|
несинусоидальной (рис. 5.9 б и в), а следовательно, немонохроматической: возникают волны различных частот из первоначального гармонического колебания.


506 Упругие волны [ Гл. 5
и из 6162E
0
Окончательно получаем (так как 2$ , 0 2$ 0):
0 1 |
|
(5.48) |
7 |
|
|
Изменение частоты колебаний, регистирируемых неподвижным приемником при движении источника (5.46), либо изме-
нение частоты, регистрируемой движущимся приемником при неподвижном источнике (5.48), называется эффектом Допле-
ра (по имени австрийского физика и астронома К. Доплера (1803–1853)).
Как следует из сравнения этих формул, не безразлично, что движется относительно среды — источник или приемник, однако при малых скоростях обе формулы дают одинаковый результат.
Задачи
1. По заданному графику мгновенного распределения смещений H по длине стержня (рис. 5.12 а) постройте график скоростей и деформаций 0 для волны, бегущей слева направо и справа налево.
|
|
z |
t |
O |
O |
à |
á |
Рис. 5.12
2.По заданной осциллограмме смещений H (в фиксированной плоскости, рис. 5.12 б) постройте осциллограммы скорости и деформации (напряжения) в волне, бегущей слева направо.
3.По стержню распространяются две встречные волны одинаковой частоты и амплитуды. Найдите результирующую волну смещений H , , скоростей, и деформаций 0 , Изобразите графики и 0 при фиксированном .
4.Изобразите моментальные снимки распределения деформации 0 и скорости в волне сжатия, бегущей по стержню, если соответствующий
|
|
|
|
|
|
|
|
|
|
|
|
снимок смещений H имеет вид, по- |
|
|
|
|
|
|
|
|
|
z |
казанный на рис. 5.13 а. |
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
v |
|
|
O |
|
|
5. |
Решите ту же задачу для вол- |
|||
|
|
|
|
|
|
|
|
|
ны разрежения (рис. 5.13 б). |
||||
|
|
|
|
|
|
|
|
v |
|
|
|||
|
|
|
|
|
z |
|
|
|
|
|
6. |
Найдите изменение скорости |
|
|
|
|
|
|
|
|
|
|
|
||||
|
O |
|
|
|
|
|
|
|
|
|
|
звука в воздухе при изменении тем- |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
à |
|
|
á |
|
|
|
пературы от 10 Æ до 20 Æ . |
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Рис. 5.13 |
|
|
7. |
Вычислите скорость звука |
||||
|
|
|
|
|
|
|
в стальном стержне. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
8.Выведите формулу (5.13) для скорости звука в идеальном газе.
9.Найдите мгновенное распределение потока энергии в бегущей волне H , как функции координаты ; постройте график зави-

5.9 ] Задачи 507
симости , - и 6 Найдите точки максимумов и минимумов потока энергии.
10. Покажите, что средний за период колебания поток энергии в бегущей волне H одинаков через любое сечение и равен
|
|
1 |
|
1 |
|
|
|
|
|
5 , |
*2 |
(5.49) |
|||
5 |
|||||||
|
2 |
||||||
|
|
0 |
|
|
|||
|
|
|
|
|
|
11. Найдите поток энергии, протекающий через единичное сечение за один период колебания.
Ответ: 5 2*
12.Найдите скорость смещения и деформацию 0 как функции и
встоячей упругой волне.
13.Найдите поток энергии в стоячей волне как функции координаты и времени ; найдите расстояние между сечениями , поток энергии через которые равен нулю в любой момент времени. Найдите полную энергию стоячей волны между двумя ближайшими сечениями, поток энергии через которые равен нулю. Каков закон изменения во времени кинетической и потенциальной энергии, заключенной между ближайшими сечениями, поток энергии через которые равен нулю.
14.Постройте графики мгновенных распределений скоростей , вдоль оси стержня в моменты времени 0, 4, 3 4 для типов колебаний с индексами 1, 2, 3.
15.Постройте графики мгновенных распределений деформаций 0 , вдоль оси стержня в моменты времени 0, 4 и 3 4 для тех же типов колебаний.
16.Каковы осциллограммы (зависимости от времени) скоростей и
деформаций 0 в фиксированном сечении 4 для типов колебаний
1, 2, 3.
17.Постройте осциллограммы скоростей и деформаций в сечениях4 и 3 4 для типов колебаний 1, 2, 3.
18.Показать, что сумма потоков энергии в отраженной и прошедшей волнах равна потоку энергии в падающей волне.
19.Показать, что при %1*1 %2*2, , 1 и 0, 1, т. е. вся энергия проходит во вторую среду — отражения нет.
20.Показать, что при , 0 и , , 1, 0, т. е. нет прошедшей волны — вся энергия возвращается в первую среду.
21.Показать, что коэффициенты отражения и прохождения не зависят от того, с какой стороны волна падает на границу раздела двух сред.
22.Используя (5.39), покажите, что 2 всегда имеет тот же знак, что и1, т. е. колебания в прошедшей волне на границе 0 происходят синфазно
сколебаниями в падающей волне.
23.Показать, что на границе 0 колебания в отраженной волне проис-
ходят синфазно с колебаниями в падающей волне ( 1 и 1 имеют одинаковый
знак), если , G 1. Если же , 1 2 E 1, то 1 и 1 имеют разные знаки, т. е. колебания в отраженной волне происходят в противофазе с колебаниями
впадающей волне.
24.Как зависит константа , от плотности % и модуля упругости * первой и второй среды?
25.Рассмотрите предельные случаи , 0 и , (когда нет прошедшей
во вторую среду волны и 1 1). Покажите, что при этом в первой среде возникает стоячая волна с пучностью смещений на границе 0, если , 0,
и узлом на той же границе, если , . Какой из этих случаев реализуется, когда звуковая волна в воздухе падает на границу с металлом?

6.1 ] |
Уравнения Максвелла и волновое уравнение |
509 |
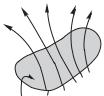
тянутую на контур (рис. 6.2), — производная по времени поля B.
Во-вторых, переменное электрическое поле является источником магнитного поля :
|
|
(6.2) |
|
|
|
В левой части последнего равенства — циркуляция магнитного поля H по произвольному замкнутому контуру, в правой части — скорость изменения потока вектора
D через поверхность 9 ( — производная по |
B |
|
|
|
времени поля ). |
|
|
|
|
Так и рождаются электромагнитные вол- |
|
|
|
|
ны: если в какой-либо точке пространства |
|
|
óð |
l |
возникло меняющееся электрическое поле |
|
îíò |
|
|
(E 0), то в соответствии с (6.2) возни- |
Ê |
|
|
|
|
|
|
||
кает магнитное поле, которое, изменяясь во |
Поверхность S |
|
|
|
времени, порождает в соответствии с (6.1) |
Рис. 6.2 |
|
электрическое поле. Так, взаимно индуцируя |
||
|
друг друга, возникают меняющиеся во времени электрическое и магнитное поля — возникает электромагнитная волна. Почему именно волна? Как это следует из законов (6.1) и (6.2)?
Мы рассмотрим наиболее простую ситуацию: однородную изотропную среду, свойства которой характеризуются двумя параметрами: константами < (диэлектрическая проницаемость среды) и 1 (магнитная проницаемость). Как известно, эти величины связывают между собой поля и ; и (так называемые
материальные уравнения): |
|
<0< , 101 |
(6.3) |
Напомним, что равенства (6.3) не являются универсальными и справедливы лишь для линейной среды, свойства которой не
зависят от того, имеются ли в среде поля или их нет, велики эти поля или малы. В рассматриваемой нами среде нет токов, поэтому в правой части уравнения (6.2) отсутствует слагаемое, содержащее токи проводимости. Полагаем также, что среда является изотропной, т. е. свойства среды (< и 1) не зависят от ориентации в пространстве электрического и магнитного поля
и .
Будем полагать далее, что поля и (а значит, и и ) зависят лишь от одной координаты, например, координаты и, разумеется, от времени:
, , ,
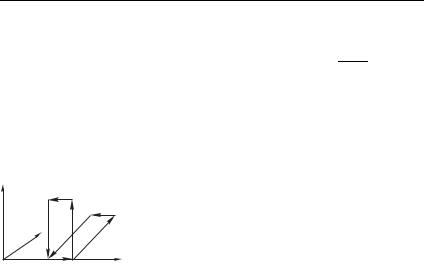
510 |
|
Электромагнитные волны |
|
|
|
[ Гл. 6 |
|||||||
Это означает, что в любой плоскости величина |
|||||||||||||
поля (как и ) одна и та же в любой фиксированный момент |
|||||||||||||
времени во всех точках этой плоскости. Используя (6.3), пере- |
|||||||||||||
пишем уравнение (6.2), введя обозначение |
1 <010 , в виде |
||||||||||||
|
|
|
|
|
0! |
|
|
, |
|
|
|
(6.4) |
|
|
|
|
|
|
|
72 |
|
|
|
|
|||
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
константы < и 1 вынесены из-под знака интегралов. Применим |
|||||||||||||
уравнения (6.1) и (6.2) к контуру %E, в котором %E |
|||||||||||||
y |
|
|
и |
E % . Контур |
%E |
||||||||
M |
|
лежит в плоскости (рис. 6.3; стрелками |
|||||||||||
N |
|
||||||||||||
|
B |
C |
показано положительное направление об- |
||||||||||
x |
|
|
хода). Мы получаем |
|
|
|
|
||||||
|
|
z |
- - , |
||||||||||
|
|
|
|||||||||||
A |
D |
|
|
|
|
|
|
|
|
|
0! |
|
(6.5) |
Рис. 6.3 |
|
72 |
- |
||||||||||
Вклад в контурный интеграл участков E и % бесконечно |
|||||||||||||
мал при 0. Разделив левые и правые части равенств (6.5) |
|||||||||||||
на и переходя к пределу при 0, находим: |
|
|
|||||||||||
|
|
* , |
|
|
0! |
|
* |
|
(6.6) |
||||
|
|
|
|
|
|
|
72 |
|
|
|
|
||
Аналогичным образом, применив уравнения (6.1) и (6.2) к |
|||||||||||||
контуру E ! (этот контур лежит в плоскости , ! |
|||||||||||||
E ), получаем |
|
|
|
|
|
|
|
|
|
|
|||
|
|
* |
, |
|
|
0! |
|
* |
|
(6.7) |
|||
|
|
|
|
|
|
|
|
72 |
|
|
|
|
|
Выпишем отдельно пару уравнений из (6.6) и (6.7), содержа- |
|||||||||||||
щих только поля - и : |
|
|
|
|
|
|
|
|
|
||||
|
* , |
|
0! |
* |
|
(6.8) |
|||||||
|
|
|
|
|
|
|
|
|
72 |
|
|
|
|
Другая пара содержит поля - и : |
|
|
|
|
|
||||||||
|
|
* , |
|
0! |
* |
|
(6.9) |
||||||
|
|
|
|
|
|
|
|
|
72 |
|
|
|
|
Мы видим, что пара полей - , совершенно не связа- |
|||||||||||||
на с другой парой - , , |
т. е. изменяющиеся во |
времени |
|||||||||||
и пространстве поля - |
и |
могут существовать совершенно |
|||||||||||
независимо от другой пары - |
и . Рассмотрим одну из этих |
||||||||||||
