
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf12.2 ] |
Понятие плазмы |
371 |
разряда: поля, потенциала, концентрации частиц, всех основных
процессов — да и чисто визуальная.
Коронный разряд («огни святого Эльма») образуется обычно на остриях и тонких проволочках. Его отличает еще б´ольшая пространственная неоднородность, так что лишь в некоторой области пространства вблизи острия идет самостоятельный разряд, а в остальном пространстве пробоя газа не происходит, и ток
через газ просто «навязан» областью пробоя.
Для искрового разряда (в частности, и молнии) характерны очень сильные поля и короткие характерные времена. Разряд происходит по треку предварительно образовавшегося канала, т. н. стримера. За его образование отвечают множественные электронные лавины, развитие которых происходит не совсем так, как в тлеющем разряде. Начало лавине дает акт фотоионизации фотоном, испущенным какой-то предыдущей лавиной. Поскольку фотоны, в отличие от электронов, распространяются со скоростью света, развитие стримера идет намного быстрее,
чем единичной электронной лавины.
Для дугового разряда характерны, напротив, большие токи и сравнительно небольшие значения падения напряжения. Электроны, поддерживающие ток, поставляются термоэлектронной эмиссией с катода (возможна, впрочем, и «холодная» дуга). Здесь важную роль играет материал электродов, испаряющийся и ионизующийся в процессе разряда.
Существует немало и других режимов. Сколько-нибудь детальное их рассмотрение едва ли уместно в общем курсе физики. Отметим как общее свойство всех разрядов следующее обстоятельство. В процессе газового разряда вещество превращается в плазму — агрегатное состояние, располагающееся выше, чем газ, на температурной шкале. Для перехода в состояние плазмы по обычному каналу фазовых переходов необходимо нагреть вещество до температуры 5 000–10 000 К, что как раз соответствует характерной температуре поверхности Солнца и звезд. Газовый разряд, ввиду исключительной его неравновесности, позволяет осуществить этот переход более дешевой ценой при гораздо более умеренных температурах и поддерживать вещество в этом состоянии также относительно простым и доступным способом.
12.2. Понятие плазмы
Плазму нередко определяют как ионизованный газ. Это верно по сути, но с равным успехом и газ можно определить как испаренную жидкость, а последнюю — как расплавленное твердое тело. При достаточно высокой степени ионизации газ, как мы вскоре убедимся, приобретает существенно новые свойства,
372 |
Элементы физики плазмы |
[ Гл. 12 |
позволяющие с полным основанием говорить о новом агрегатном состоянии. Правда, поскольку ионизация — процесс непрерывный и может быть проведен адиабатически медленно, здесь нет выраженного фазового перехода.
Газовый разряд — сугубо неравновесный канал превращения газа в плазму. В равновесном состоянии плазма — объект весьма
высокотемпературный. Поэтому температуру ее обычно измеряют в «атомных» энергетических единицах — электронвольтах:
1 эВ D 1 В 1,6 10 19 Дж 11 600 К
Энергия ионизации атома водорода равна примерно 13,6 эВ; температура плазмы в современных лабораторных установках, предназначенных для исследований по управляемому термоядерному синтезу, достигает 103–104 эВ, тогда как температура поверхности Солнца — всего лишь около 0,5 эВ. Такую плазму называют холодной.
Может возникнуть вопрос: как может вещество в равновесном состоянии полной или почти полной ионизации иметь температуру, на порядок меньшую энергии ионизации? Дело в том, что ионизация поддерживается относительно малой долей высокоэнергичных частиц — «хвостами» функции распределения по скоростям.
Для сравнения укажем, что для излучения фотона в красной области спектра энергия возбуждения излучающего атома должна превышать 1,5 эВ, но температура красного каления обычно заметно ниже 0,1 эВ.
Ввиду высокой степени равновесной ионизации плазма, в отличие от газа при умеренной температуре, оказывается очень хорошим проводником. Даже холодная плазма поверхности Солнца по проводимости приближается к металлам, а высокотемпературная термоядерная плазма по этому параметру значительно их превосходит. Например, проводимость водородной плазмы при температуре 10 кэВ примерно в 20 раз выше, чем у меди при нормальных условиях. В то же время плазма — среда текучая. Отсюда следует первое отличие плазменной фазы от газовой: у нее невозможно разделить механические и электродинамические свойства. Электромагнитные поля вызывают течение плазмы и управляют им, и напротив, течение плазмы порождает электромагнитное поле.
Мы уже рассматривали в гл. 7 силы, действующие на проводник в магнитном поле, и, в частности, установили, что в случае прямых силовых линий и нулевого поля в проводящей среде на
поверхность проводника действует давление (см. (7.1)) |
|
||||
|
|
|
2 |
|
(12.6) |
|
|
||||
|
2!0 |
|
|
||
|
|
|
|
||
12.2 ] |
Понятие плазмы |
373 |
Мы положили 1 1, |
что для плазмы, как и |
для газа, все- |
гда верно с очень хорошей точностью. Именно для горячей плазмы эффект магнитного давления особенно выразителен. Во-первых, из-за высокой проводимости коэффициент диффузии поля E 1 10 будет очень мал. А во-вторых, малы и харак-
терные времена плазменного эксперимента: от 10 8 до 10 3 с. Как следствие, эффективная глубина проникновения поля в плазму (см. оценку (8.27)) может быть много меньше характерного размера плазменного облака.
Отсюда следует возможность магнитного удержания плазмы. Дело в том, что высокотемпературную плазму нельзя непосредственно заключить в твердый сосуд — ее погубит рекомбинация на стенках; скажем, в случае водородной плазмы H D H. Поэтому плазму обычно удерживают бесконтактным методом — «магнитной стенкой» (соответственно, ее можно толкать «магнитным поршнем»). Создается конфигурация поля, в которой плазменное облако оказывается как бы в яме в некоторой окрест-
ности минимума 2 . Такие устройства называются магнитными ловушками. Разумеется, одно лишь магнитное давле-
ние (12.6) равновесия обеспечить не может. Необходимо учесть также газокинетическое давление плазмы Б , где Б — постоянная Больцмана. Условие равновесия, включая и пограничный слой, где поле проникает в плазму, есть условие постоянного полного давления:
2 |
|
(12.7) |
Б 2!0 |
|
|
Препятствуют равновесию, помимо диффузии поля, еще и многочисленные неустойчивости, исследование которых представляет собой довольно заметную часть вообще всей физики плазмы. В большинстве экспериментальных ситуаций макроскопическая динамика плазмы тождественна так называемой магнитной гидродинамике, которая, в частности, описывает равновесие и течение жидких металлов. Таким образом, хотя плазма и располагается по температурной шкале выше газов, по своим электромеханическим свойствам она оказывается близка конденсированному веществу и заметно отличается от газа.
Рассматривая электромагнитные поля в плазме, мы не можем считать 3 и заданными извне — они должны определяться самосогласованным образом как функции электрического и магнитного полей. Поскольку плазма, как и газ, — среда бесструктурная, заряды и токи, наведенные полями, представляют собой просто свободные заряды и токи проводимости. Поэтому их можно прямо включить в уравнения Максвелла, и не делая различия по физике между полем и индукцией, т. е. положив < 1 1, оставить в базовых уравнениях только действующие

374 Элементы физики плазмы [ Гл. 12
поля E и B: |
|
|
||||
|
|
|
1 |
3 ; |
|
(12.8) |
|
|
|||||
00 |
|
|
|
|||
|
|
0; |
|
(12.9) |
||
|
|
; |
|
(12.10) |
||
|
|
|
||||
1 |
<0 |
|
(12.11) |
|||
|
|
|
||||
|
!0 |
|||||
К числу наиболее важных свойств плазмы относится квазинейтральность.
Представим себе, что некоторое количество газа переводится тем или иным способом в состояние, полностью или частично ионизованное. При этом полный заряд его остается равным нулю.
В принципе, возможно существование и заряженной плазмы (пример — облако пространственного заряда в электронной лампе). Но оказывается, что для систем с выраженными плазменными свойствами как в природе, так и в лабораторных условиях свойство нейтральности в целом гораздо более типично. Более того, плазма достаточно высокой концентрации оказывается нейтральной и в локальном смысле:
. F , |
(12.12) |
где ., — концентрации компонентов, а F — заряд иона (кратность ионизации), который в дальнейшем мы для простоты будем считать равным единице (для водородной или дейтериевой
плазмы это вообще единственная возможность). Именно свойство (12.12) и называется квазинейтральностью. Оно опреде-
ляет многие специфические для плазмы физические эффекты и свойства.
Покажем на типичном примере, почему квазинейтральность трудно нарушить в макроскопических масштабах.
Возьмем кубик объемом 2 1 см3 и предположим, что его заполняет плазма, достаточно типичная для лабораторных экс-
периментов:
. 1020 м 3
Пусть мы хотим нарушить равенство концентраций в данном объеме всего на один процент, т. е. создать избыток концентрации любого из компонентов
Æ 0,01 1018 м 3
Оценим возникающее при этом электрическое поле, используя теорему Гаусса:
|
- |
9 |
5 |
Æ <" |
|
||||
|
|
00 |
00 |
|

12.3 ] Ленгмюровские колебания и дебаевское экранирование 375
Вычисления дают - 3 107 В/м. Можно той же оценке придать и другой смысл. Пусть кубик нейтрален в целом,
. ,
но попытаемся нарушить локальное равенство (12.12), например, у одной грани кубика пусть будет . 10 2 ., , а у другой 10 2. Получим ту же цифру. В первом случае электростатическое отталкивание эквивалентно огромному добавочному давлению, взрывающему объем, заполненный плазмой, а во втором притяжение разноименных зарядов эффективно выравнивает локальную плотность заряда. И в обоих случаях, чтобы поддержать нашу систему в неравновесном состоянии, необходимы внешние поля, не меньшие, чем 107 В/м. Если же внешнее поле такого порядка величины не достигает, условие (12.12) в нашем конкретном случае будет выполнено с точностью Æ 0,01 ,.
Конечно, само определение локальной концентрации подразумевает некоторое усреднение числа частиц по пространству и по времени. Поэтому и утверждение о квазинейтральности не может быть абсолютным, хотя бы из-за дискретности вещества. Однако, как мы увидим в следующем параграфе, главный фактор нарушения квазинейтральности, а тем самым и масштабы такого усреднения связаны с движением частиц плазмы.
|
|
12.3. Ленгмюровские колебания и |
|
|
||||
|
|
|
дебаевское экранирование |
|
|
|
|
|
Попытаемся оценить минимальный масштаб времени, ниже |
||||||||
которого квазинейтральность не может быть обеспечена. Рас- |
||||||||
смотрим плоский слой плазмы и дадим в нем всем электронам |
||||||||
смещение |
относительно ионов |
в перпен- |
|
x |
|
|
||
дикулярном слою направлении (рис. 12.3). |
|
|
|
|||||
|
|
|
|
|||||
Если |
|
— |
пространственное |
смещение |
|
|
||
|
|
|
|
|||||
, то заряд на единицу площади в уз- |
|
E |
|
S 1 |
||||
ких приграничных слоях оказывается рав- |
|
|
|
|
||||
ным ; D Поле каждой из двух парал- |
|
|
|
|
||||
|
|
|
|
|||||
лельных заряженных плоскостей равно, со- |
|
|
|
|
||||
гласно (1.11), ;2<0; вне плазменного слоя |
|
l |
|
|
||||
эти поля компенсируют друг друга, а внутри |
|
|
|
|
||||
слоя складываются (все это очень напоми- |
|
|
|
|
||||
нает плоский конденсатор). Таким образом, |
|
|
|
|
||||
электрическое поле в слое |
|
|
Рис. 12.3 |
|
||||
|
|
|
- < |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
00 |
|
|
|
|
|

376 |
Элементы физики плазмы |
[ Гл. 12 |
Принимая во внимание соотношение масс . 1 (почти |
||
2 000 даже |
для водорода), пренебрегаем смещением |
ионов, и |
тогда электронное уравнение движения оказывается очень простым:
|
2 |
<2 |
|
|
(12.13) |
|
|
D- |
|
||||
|
2 |
|
|
|
||
|
00 |
|
|
|
||
Это уравнение гармонических колебаний, частота которых равна
|
<2 |
1 2 |
|
0. |
|
(12.14) |
|
00 |
|
||
|
|
Колебания электронов относительно ионов, которые мы таким образом получили, называются ленгмюровскими (по имени аме-
риканского физика И. Ленгмюра (1881–1957)) или просто плазменными колебаниями. Последнее обстоятельство подчеркива-
ет очень важную роль, которую играют движения такого рода
в микроскопической динамике плазмы. Частота (12.14) называется соответственно электронной плазменной или электронной ленгмюровской частотой.
Поскольку электроны как целое могут пермещаться относительно ионов, постольку может нарушаться квазинейтральность, но лишь на очень короткое время, порядка периода плазменных колебаний. Следовательно, масштаб усреднения по времени, подразумеваемый в формуле квазинейтральности (12.12), может
быть оценен как
0.1
Определение пространственного масштаба усреднения потребовало бы привлечения определенных сведений из термодинамики (см. раздел 5), да и формальная сторона дела связана с достаточно сложной вычислительной процедурой. Но сам результат может быть продемонстрирован без особых затруднений на основании одних лишь соображений размерности. Наиболее характерная величина размерности скорости в микродинамике любой текучей среды (жидкость, газ, плазма) — тепловая скорость частиц, в данном случае — электронов: Б Отношение ее к плазменной частоте как раз и дает величину размерности длины, а в теории плазмы именно эта величина
оказывается характерным масштабом разделения зарядов. Ее называют дебаевской длиной или дебаевским радиусом, по имени
голландского физика П. Дебая (1884–1966):
|
|
|
00 Б |
(12.15) |
|
D |
|
<2 |
|||
|
|||||
Масштаб пространственного усреднения в (12.12) должен быть существенно больше D . Но существует еще один характерный

12.4 ] Электромагнитные волны в плазме 377
масштаб нарушения квазинейтральности, упомянутый выше, — это просто характерное расстояние между частицами 1 3 Соотношение между этими двумя масштабами оказывается принципиально важным для микроскопических свойств плазмы. Дело в том, что если D 1 3, то, в отличие от газа, где взаимодействие частиц сводится к достаточно редким столкновениям, частицы плазмы достаточно эффективно взаимодействуют в соответствии с законом Кулона.
В обратном случае кулоновское поле экранировано вследствие квазинейтральности, и тогда микродинамика плазмы лишь количественно отличается от газовой. Обычно из названных па-
раметров образуют безразмерную комбинацию, которую называют числом частиц в дебаевской сфере или просто дебаевским
числом: |
4 |
|
3 |
3 2 |
|
|
||||
|
|
4 00 Б |
(12.16) |
|||||||
!D |
|
|
|
|
|
|
|
|
||
3 |
D 3 |
|
<3 |
|||||||
|
|
|
||||||||
Если !D 1, то в сфере действия кулоновского потенциала каждой частицы оказывается большое число других частиц. В этом случае коллективные эффекты, т. е. согласованные движения ансамблей частиц, превалируют над столкновениями. Эта ситуация очень далека от газа, и даже от жидкой фазы, но напоминает скорее твердое тело — кристалл. Таким образом, и в макро-, и в микродинамике плазма, будучи более высокотемпературной фазой, нежели газ, обнаруживает свойства, присущие конденсированным средам, что и дает основания говорить о четвертом состоянии вещества. Из (12.16) можно видеть, что условие !D 1 может быть выполнено для плазмы либо достаточно горячей, либо достаточно разреженной. Поэтому удовлетворяют этому условию объекты столь различной природы, как «термоядерная» плазма в лабораторных условиях и холодная, но очень редкая плазма межзвездной среды.
12.4.Электромагнитные волны в плазме
Вданном параграфе будет рассмотрена поперечная электромагнитная волна в плазме. Как мы вскоре убедимся, плазма для такой волны — диспергирующая среда, т. е. закон дисперсиибудет отличен от линейного. Поле волны представим в стандартной форме
0 !
В горячей плазме (1–10 кэВ или, что то же, 10–100 106 К) столкновения частиц настолько редки, что безусловно доминируют коллективные эффекты. Проще говоря, мы можем рассматривать отклик ансамбля частиц на быстропеременное электромагнитное поле, совершенно не принимая во внимание какой-либо

378 |
Элементы физики плазмы |
[ Гл. 12 |
диссипации. Относительно частоты осцилляций мы предположим, что за период ионы существенно сместиться не могут и успевают отреагировать на изменение поля лишь электроны. Напишем уравнение движения электронов в поле волны
|
2 |
|
D 0 ! |
(12.17) |
|
|
2 |
||||
|
|
|
|
||
Здесь под , , подразумевается лишь осцилляция электрона в волне. (Мы пренебрегли в (12.17) членом , поскольку в случае нерелятивистского движения частицы он дал бы малую поправку к правой части порядка .) Уравнение (12.17) легко интегрируется:
|
< |
|
! |
(12.18) |
|
|
2 |
||
|
0 |
|
||
|
|
|
|
Далее в соответствии с соотношениями (2.8), (2.9) запишем общее выражение для диэлектрической проницаемости
<0< <0 , |
(12.19) |
в котором поляризация среды представляется объемной плотностью дипольного момента
/' '
'
Для его вычисления воспользуемся решением (12.18). Пусть — число электронов в единице объема, тогда
D <2 2 ,
00
откуда и следует
2
< 1 , (12.20)
2
где величина 0. — уже известная нам ленгмюровская или плазменная частота (12.14).
Теперь воспользуемся выражением (11.3) для показателя преломления электромагнитной волны в среде:
!2 |
272 |
|
(12.21) |
2 |
<1 |
|
|
(Поскольку — стандартное обозначение концентрации, нам пришлось обозначить показатель преломления буквой !.) Положим опять 1 1 Получаем закон дисперсии
272 |
|
1 |
2 |
, |
(12.22) |
||||
|
|
2 |
|
|
2 |
|
|
||
или, что то же, |
|
|
|
|
|
|
|||
2 2 2 |
2 |
(12.23) |
|||||||
|
|||||||||
|
|
0. |
|
|
|
||||
12.4 ] |
|
Электромагнитные волны в плазме |
|
379 |
||
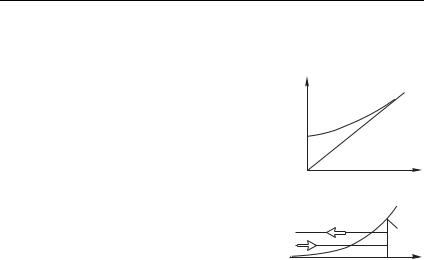
Дисперсия (12.23) представлена на рис. 12.4 а. Видно, что в пре- |
||||||
деле высоких частот мы приближаемся к «вакуумному» линей- |
||||||
ному закону , но при 0 ситуация иная; в частности, |
||||||
распространение в плазме электромаг- |
|
|
|
|||
нитных волн с ' 0. невозможно. |
|
kc |
||||
Закон дисперсии (12.23) имеет ме- |
|
|||||
|
|
|
||||
сто не только в плазменном случае, но |
|
|
|
|||
и, скажем, |
при распространении волн |
pe |
|
|
||
в волноводах и, что для нас более су- |
|
|
||||
|
|
|
||||
щественно, |
он |
справедлив для любого |
|
|
k |
|
вещества при |
достаточно высоких ча- |
|
|
|||
|
à |
|
||||
стотах (при этом 0. определяется фор- |
|
|
||||
|
|
n(x) |
||||
мально через концентрацию электронов |
|
|
||||
|
|
|
||||
в веществе). Это |
не так уж и удиви- |
|
0 |
|
||
тельно, поскольку |
чисто электронный |
|
nêð |
|||
0 |
|
|||||
отклик на поле высокой частоты вполне |
|
x |
||||
|
|
|||||
естествен. Даже у водорода отношение |
|
á |
|
|||
масс . 1 840, а отклик на по- |
|
|
||||
|
|
|
||||
ле (см. (12.18)) обратно пропорциона- |
Рис. 12.4 |
|
||||
лен массе. Но если для плазмы порядок |
|
|
|
|||
минимальной частоты такого поля определяет именно 0., то |
||||||
в общем случае ответ не универсален, поскольку не ясна заранее |
||||||
роль диссипативных эффектов, которыми мы пренебрегли. |
|
|||||
Опираясь на соотношение (12.22), мы можем рассмотреть |
||||||
эффект отражения волны от плазмы критической плотности. Об- |
||||||
ратимся к рис. 12.4 б. Пусть в плазму с монотонно нарастающей |
||||||
плотностью (или электронной концентрацией) посылается |
||||||
электромагнитная волна. Следуя в направлении роста концентра- |
||||||
ции, волна сохраняет частоту 0, но длина волны или волновое |
||||||
число при этом сохраняться не могут. При |
& кр |
2 |
2 |
|||
<0 0D |
||||||
эта волна вообще существовать не может. Но она не может и |
||||||
исчезнуть, поскольку никаких механизмов диссипации мы в рас- |
||||||
смотрение не вводили. Обратим внимание на то, что в области |
||||||
критической концентрации кр, как следует из (12.23), 0, а |
||||||
при меньших концентрациях, согласно той же формуле, опре- |
||||||
делено с точностью до знака. Отсюда и следует, что наша волна |
||||||
должна просто отразиться от области критической концентрации |
||||||
и выйти в обратном направлении. |
|
|
|
|||
Именно на этом эффекте основана дальняя радиосвязь на |
||||||
коротких волнах — точнее, на многократном отражении волны |
||||||
от поверхности Земли и ионосферного плазменного «зеркала» |
||||||
(рис. 12.5). А вот на УКВ, как известно, связь возможна только |
||||||
в пределах прямой видимости. Тем и отличаются ультракороткие |
||||||
волны от коротких, что у них частота выше максимальной плаз- |
||||||
менной частоты для ионосферы. |
|
|
|
|||

380 |
Элементы физики плазмы |
|
[ Гл. 12 |
||||
|
Мы уже упоминали в гл. 11, что для достаточно жестких (ко- |
||||||
ротковолновых) рентгеновских лучей коэффициент преломления |
|||||||
|
|
любого вещества |
оказывает- |
||||
Ионосфера |
ся близок к единице. Имел- |
||||||
ся в виду закон диспер- |
|||||||
сии (12.22). Заметим еще раз, |
|||||||
|
|
||||||
|
|
что |
соответствующий |
такой |
|||
|
|
дисперсии |
коэффициент |
пре- |
|||
|
|
ломления |
меньше |
единицы. |
|||
|
|
Поэтому и полное отражение |
|||||
|
Рис. 12.5 |
оказывается не внутренним, |
|||||
|
как в оптике, а внешним. Это |
||||||
|
|
||||||
используется для создания «рентгеноводов». В отличие от све- |
|||||||
товода — стеклянной нити — рентгеновод представляет собой |
|||||||
полую кварцевую трубочку. Принцип его работы тот же, что и |
|||||||
у световода, — многократное полное отражение. И еще один эф- |
|||||||
фект такого рода — металлический блеск. Здесь уже дело касает- |
|||||||
ся квантовой плазмы электронов проводимости. (Хотя, конечно, |
|||||||
следует заметить, что чисто плазменным эффект отражения от |
|||||||
металлов оказывается лишь в инфракрасной области — будь это |
|||||||
так же и в оптическом диапазоне, все металлы были бы белыми, |
|||||||
включая золото и медь). |
|
|
|
|
|
||
|
Нарисовав картинку и следя за распространением вол- |
||||||
ны, мы молчаливо предполагаем, что длина волны 2$ су- |
|||||||
щественно меньше характерного масштаба неоднородности. Но |
|||||||
это предположение нарушается, по крайней мере, вблизи кр, |
|||||||
где 2$ . В этой области осциллирующее поле сшивается |
|||||||
с экспоненциально затухающим решением при одном и том же |
|||||||
характерном масштабе 0.. Называют его бесстолкновитель- |
|||||||
ной скиновой длиной, которая, как нетрудно видеть, зависит |
|||||||
только от концентрации электронов, но не от частоты поля или |
|||||||
проводимости среды. |
|
|
|
|
|
||
|
В заключение заметим, что в плазме могут распространяться |
||||||
не только поперечные, но и продольные электромагнитные вол- |
|||||||
ны. Действительно, при отличной от единицы диэлектрической |
|||||||
проницаемости уравнение (10.17) можно переписать в виде |
|||||||
2 2
! ! 0 ! ! 0 0 10<<0 0
Предположим, что ! . Тогда левая часть оказывается в точности равной нулю, и получившееся простое уравнение допускает два решения — тривиальное 0 и содержательное
< , ! 0 |
(12.24) |
Уравнение (12.24) представляет общий вид дисперсионного уравнения для продольных волн. В частности, приравнивая нулю
