студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy

11.5 ] Электромагнитные волны и теория относительности 361

а уходящий с преломленной волной,

которое и в самом деле выполнено для коэффициентов отражения и прозрачности (11.16).

11.5. Электромагнитные волны и теория относительности

Исходя из самой процедуры вывода волнового уравнения (10.13) или (10.14), электромагнитные волны представляют собой поля E и B в вакууме и тем самым принципиально отличаются от других известных волновых движений, например, звуковых волн. Общность формального описания — волновые уравнения, их фундаментальные решения и пр. — в течение многих десятилетий побуждала физическое сообщество к поиску более глубокой физической аналогии. Поскольку звуковые волны представляют собой волновые движения в упругой твердой или жидкой среде, высказывались предположения о существовании некоторой гипотетической среды — эфира, колебания которой и описываются уравнениями Максвелла. Среда эта должна быть абсолютно упругой (прозрачной) и заполнять все физическое пространство, включая находящееся там вещество. Строились достаточно убедительные теоретические модели (автором одной из наиболее совершенных был Г. Герц), которые могли объяснить некоторую совокупность экспериментальных фактов, но рано или поздно приходили в противоречие с данными очередного эксперимента. Как особо важные следует отметить прежде всего опыты Майкельсона, экспериментально доказавшего, что скорость света не зависит от того, распространяется сигнал поили против скорости движения Земли по орбите ( 30 км/с). Параллельно был поставлен опыт Физо, впоследствии повторенный в усовершенствованном варианте Майкельсоном, из которого следовало, что закон «сложения скоростей» эфира и световых волн должен принципиально отличаться от такового в механике Ньютона.

Вопрос о сложении скоростей вообще оказался совершенно принципиальным. Напомним, что в ньютоновой механике переход между двумя инерциальными системами отсчета задается

где V — скорость новой системы отсчета относительно старой. Второе условие, в частности, декларирует, что время течет одинаково во всех инерциальных системах. В течение почти двух столетий физический эксперимент, выполненный с доступной по тому времени точностью, подтверждал адекватность преобразований (11.20).

Механика Ньютона инвариантна по отношению к преобразованию (11.20). Это и выражено по сути первым законом Ньютона, который можно прочитать следующим образом: покой есть эквивалент равномерного движения, и все законы природы одинаковы во всех инерциальных системах отсчета. Но уравнение (10.5), хотя бы оно и следовало из ньютоновой механики, отнюдь не инвариантно в смысле (11.20). В этом нет парадокса, потому что любые механические колебания привязаны к колебательной системе, а звук, соответственно, к твердой или текучей среде (под последней мы понимаем жидкость или газ). Разумеется, среди возможных систем отсчета, переходы между которыми описываются формулами (11.20), одна выделена, а именно, та, в которой среда покоится, и следовательно, для волновых движений не существует какого-либо преимущественного направления.

Предположим, эфира как такового не существует. Все известные модели его отвергнуты экспериментом. Электромагнитные волны суть поля в вакууме. Вакуум не имеет скорости, и понятие направления для него не имеет смысла. Значит, уравнения Максвелла (9.2)–(9.5) или (9.8)–(9.11) должны выглядеть одинаково во всех экспериментальных системах. Но уравнения Максвелла не инвариантны относительно преобразований (11.20)!

Описанные трудности и явились побудительным мотивом к созданию специальной теории относительности (СТО). В настоящее время ее более принято называть релятивистской механикой, и главный экспериментальный материал для ее подтверждения поставляют ядерная физика и физика элементарных частиц. На данный момент эти данные не менее убедительны, чем обоснования ньютоновой механики. Но до появления знаменитой работы Эйнштейна (1905 г.) их практически не было, зато в течение полувека информация к размышлению поставлялась оптическими измерениями. И сама работа Эйнштейна называлась «К электродинамике движущихся тел», и главным постулатом в ней — в духе сказанного выше — была независимость скорости света от (инерциальной) системы отсчета.

Как известно, последовательное развитие этой идеи вкупе с принципом эквивалентности инерциальных систем потребовало

замены преобразований Галилея более сложными преобразованиями Лоренца. Для удобства записи принято оси , направлять вдоль относительной скорости V. Тогда, вместо (11.20), получаются следующие формулы перехода:

1 " 2 72

В отличие от преобразований Галилея, время уже не является общим для всех инерциальных систем и преобразуется вместе с координатами. При 2 преобразования (11.21), (11.22) переходят в (11.20), и тем самым релятивистская механика возвращается к механике Ньютона. Аналогичный предельный переход совершают выражения для энергии и импульса свободной

частицы

5 2; 5 ,

( — масса покоя частицы), с тем, правда, отличием, что в выражении для энергии возникает аддитивная добавка 2. Иногда пользуются понятием релятивистской массы, связанной с массой покоя коэффициентом 5, и тогда выражение 2 становится универсальным; в последнее время, однако, такого раздвоения понятия массы физики предпочитают избегать.

Если бы мы просто применили (11.21), (11.22) к уравнениям Максвелла, никак не преобразуя полей, инвариантности все равно не получилось бы. Но еще в задаче 3 гл. 4 мы из физических соображений ввели преобразование электрического поля (4.27) при переходе к движущейся системе отсчета. Теперь же мы предложим (правда, без вывода) полную систему преобразования полей при произвольной относительной скорости. В тех же координатных осях

Существенно, что заряд оказывается при таких преобразованиях инвариантным, / / Электромагнитное поле, как можно видеть из (11.23), (11.24), преобразуется по закону более сложному, чем простая вектор-функция, которая подчиняется преобразованию Лоренца. Электрическое и магнитное поля оказываются связанными в этих преобразованиях и в зависимости от системы координат переходят друг в друга. Тем не менее,

формулы (11.23), (11.24) имеют вполне определенный «геометрический» смысл: величины, которые мы считали векторными, оказываются компонентами некоторого тензора — четырехмерного, поскольку он определен в пространстве , , , . Мы лишь для того отмечаем это обстоятельство, чтобы предостеречь читателя: в рамках преобразований Галилея такого преобразования полей, которое обеспечивало бы инвариантность уравнений Максвелла, найти не удастся.

Таким образом, единственная среда с 1 есть вакуум. (Разумеется, в конкретных физических задачах мы очень часто можем с приемлемой для нас точностью полагать 1 и в достаточно разреженном веществе, например в атмосферном воздухе.) Идея эфира оказалась несостоятельной, но и простые преобразования перехода между инерциальными системами для электромагнитных явлений неприменимы. Уравнения Максвелла (9.2)–(9.5) или (9.8)–(9.11) оказываются существенно релятивистскими, хотя получая их, мы этих вопросов вообще не касались. В электродинамике принципиально важную роль играют электромагнитные волны, а это объект в определенном смысле ультрарелятивистский, ибо скорость их в точности равна скорости света.

Физика XX в. накопила огромный экспериментальный материал, вполне подтверждающий СТО и, в частности, справедливость соотношений (11.23), (11.24).

Задачи

1. Определить степень поляризации преломленного света, если первичный поток неполяризованного света падает под углом Брюстера из пустоты на

поверхность стекла с показателем преломления 1,5 Решение. Из условия находим 56Æ19 Искомая величина

может быть выражена через коэффициенты прозрачности:

2. Переменное электромагнитное поле с характерной частотой создается на границе слабопроводящей диэлектрической среды с параметрами 0, !,

00 . Определить характерную глубину проникновения.

Решение. Задача тем отличается от задачи о скин-эффекте, что в этой ситуации, согласно условию, ток смещения доминирует над током проводимости. Действительно, для полей вида (10.15) это сразу следует из уравнений (9.2), (9.3):

Поэтому в данном случае мы будем иметь дело не с квазистационарным профилем тока, но с проникающей в среду электромагнитной волной. Но, в отличие от (10.15), для нее частота и волновое число не могут быть одновременно вещественными, как нетрудно усмотреть из второго уравнения (11.25). Постановка задачи соответствует пространственному затуханию волны, поэтому комплексным нужно выбрать , причем, в силу малости проводимости, относительно малой будет и мнимая часть:

0 C *, ; 0,

где — координата по направлению в глубь среды от границы. Во втором уравнении (11.25) сокращаем амплитуду E:

Из главных членов этого равенства следует, как обычно, 7; приравнивая члены первого порядка малости, получаем

!072

Таким образом, эффективная глубина проникновения, определенная через показатель экспоненты, оказывается равной

Æэф 1 2 !07

Эта величина заметно отличается от квазистационарной глубины скин-слоя (8.28). Заметим, что из условия , которое, в свою очередь, есть следствие малой проводимости, вытекает, что глубина проникновения многократно превосходит длину волны.

3. Электромагнитное излучение заданной интенсивности *2 падает по нормали из вакуума на поверхность диэлектрика с диэлектрической проницаемостью 0. Определить давление на поверхность раздела сред.

4.Естественный свет падает под углом Брюстера на поверхность стекла

споказателем преломления 1,5 Найти интенсивность *2 отраженной волны, полагая величину *2 известной.

Г л а в а 12

ЭЛЕМЕНТЫ ФИЗИКИ ПЛАЗМЫ

12.1.Газовый разряд

Вкаждом разделе общей физики существуют объекты, наилучшим образом демонстрирующие физические законы, которые

вданном разделе являются предметом рассмотрения. Так, в молекулярной физике традиционным объектом для мысленных экспериментов и частных примеров общих закономерностей является идеальный или слабонеидеальный газ, в квантовой физике — атом водорода, а затем кристалл и т. д. В электродинамике один из самых удобных объектов такого рода — состояние вещества, называемое плазмой, поскольку главные свойства вещества в состоянии плазмы задаются именно электродинамикой. При этом,

вотличие, скажем, от ионных кристаллов или электролитов, прочие законы физики оказываются в какой-то мере подчиненными, вторичными, и многие совершенно принципиальные задачи физики плазмы могут рассматриваться в рамках одной только электродинамики.

Мы начнем, однако, не с физики плазмы как таковой, но с процесса протекания тока в газе — газового разряда. Физику газового разряда нередко смешивают с физикой плазмы. Как мы увидим далее, это не вполне корректно, но четкой границы между ними и в самом деле нет. Можно сказать, что в типичных условиях газовый разряд выделен исключительной неравновесностью: объект существует лишь при определенных условиях протекания через среду электрического тока (а иногда как необходимое условие добавляется внешний источник ионизирующего излучения). Все его свойства и закономерности чрезвычайно чувствительны к режиму, заданному извне. Но поскольку газовый разряд — главный метод получения плазмы в лаборатории и наиболее доступный объект плазменной природы (не считая Солнца и звезд), следует, хотя бы кратко, остановиться на физике этого явления.

Из чего бы газ ни состоял, в состоянии, близком к равновесному, он всегда — плохой проводник. Причина вполне очевидна:

вгазе молекулы почти никак друг с другом не связаны, каждая из них совершает хаотическое (броуновское) движение, и нет сколько-нибудь эффективных механизмов переноса заряда. При прохождении мощных импульсов тока через тонкие проводники,

368 Элементы физики плазмы [ Гл. 12

статочно малых полях. Пример вольт-амперной характеристики газового разряда представлен на рис. 12.1. Для наших рассуждений ее удобнее рассматривать в локальной форме " - .

тельным, а при - & -кр — самостоятельным. Происхождение такой терминологии будет ясно из дальнейшего. Теория, описывающая столь нетривиальное поведение тока в зависимости от поля, была впервые построена английским физиком Дж. Таунсендом (1868–1957). Мы воспроизведем ее основные положения и результаты.

Главная причина неадекватности закона Ома в том, что не только усредненная величина (эф, но и рождение носителей тока существенно для физики разряда. Рассмотрим для простоты чисто электронную динамику. Внешние источники (космические лучи) рождают в единицу времени определенное число электронов. Можно было бы ожидать, что когда плотность тока достигнет такой величины, то именно столько их и будет приходить на анод; рост тока, соответствующий (12.2), прекратится, и мы как раз выйдем на участок вольт-амперной характеристики. Но такое представление оказывается слишком примитивным, тем более, оно не может объяснить эффект пробоя. На самом деле

в такой системе — катод, так как внешнее излучение эффективнее взаимодействует с конденсированным веществом, нежели с разреженным газовым наполнением. Но электроны, выбитые из анода, тут же втягиваются обратно электрическим полем, тогда

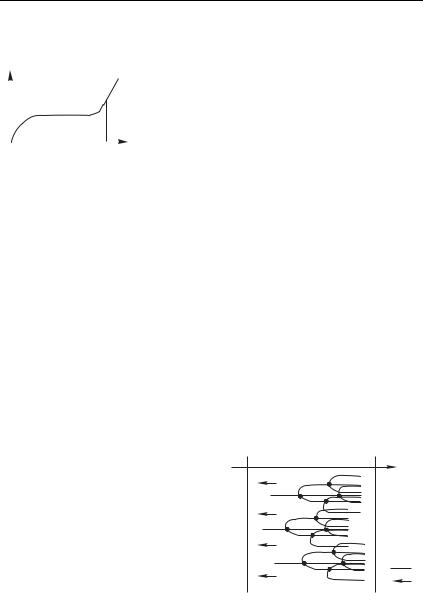
как с катода они стартуют в направлении анода. Пусть в единицу времени на катоде рождается число электронов, равное !0. Ради упрощения вычислений мы в дальнейшем пренебрегаем рождением электронов в газовом объеме. Поскольку длина пробега от нулевой скорости примерно одинакова в любой области, а практически всю энергию, полученную при ускорении в электрическом поле, электрон каждый раз отдает на вторичную ионизацию, число вторичных электрон-ионных пар на длине пробега, а значит и на единицу длины, примерно одинаково и может характеризоваться некоторым параметром *:

* B ,

где ось направлена от катода к аноду (рис. 12.2), координата катода 0, анода — . Уравнение, описывающее изменение числа электронов с координатой , следует из условия

!*

Решение его, как хорошо известно, — экспонента:

Этот процесс экспоненциального накопления электронов в ка- тод-анодном промежутке схематически показан на рис. 12.2. Для определенности мы «привязали» вторичные электроны к самому концу свободного пробега. Напомним еще раз, что число электронов у нас нормировано на единицу времени. Чтобы получить число вторичных электрон-ионных пар, нужно вычесть из (12.3) число электронов, порождаемое в единицу времени внешним

источником:

! ! 0 * 1

В установившемся режиме разряда именно таким будет число ионов, приходящих в единицу времени на катод. Они не слишком эффективны в процессе объемной ионизации — из-за их малых скоростей, однако из массивного катода они могут выбивать вторичные электроны — для этого энергии у них достаточно. Пусть каждый из них выбивает в среднем 5 вторичных электронов. (Заметим, что коэффициенты * и 5 могут быть как больше, так и меньше единицы.) Тогда число электронов, выбитых ионами из катода в единицу времени, равно

5! 0 * 1 ,

а полное их число, образованное ионами и внешним источником в единицу времени

! 0 !0 5! 0 * 1

370 Элементы физики плазмы [ Гл. 12

Если знаменатели в формулах (12.4) положительны, мы имеем дело с несамостоятельным разрядом, поскольку : !0, но

если мы достигаем критического условия

5 * 1 1,

то величина !0 уже несущественна, поскольку полный ток

в (12.4) формально обращается в бесконечность. Это и есть пробой, иными словами — переход в режим самостоятельного разряда.

Почему это происходит при росте напряженности поля (рис. 12.1)? Экспериментально установлено, что «коэффициент размножения» * (на рис. 12.2 он равен трем) есть некоторая монотонная функция отношения поля к давлению газа:

* -

Таким образом, по мере роста поля или снижения давления мы и попадаем в режим самостоятельного разряда:

В отличие от несамостоятельного, самостоятельный разряд уже не нуждается во внешнем ионизаторе; последний, однако, играет важную роль в процессе зажигания. Как следствие, для вольт-амперных характеристик самостоятельных разрядов характерен гистерезис: напряжение гашения всегда ниже напряжения зажигания.

Теория Таунсенда дает правильное представление о несамостоятельном разряде (его часто и называют таунсендовским) и о переходе в режим самостоятельного разряда, но после-

дующая динамика разряда уже никак не будет универсальной. Прежде всего, в различных режимах (которые зачастую зависят не только от величины поля -, но и от «сценария» зажигания разряда) весьма различными оказываются режимы поддержания

самостоятельного разряда.

В тлеющем разряде, хорошо нам известном по газоразрядным трубкам, картина явления в наибольшей степени близка той, которую мы только что рассмотрели. Главную роль в поддержании разряда играют ударная ионизация в объеме газа и вторичная эмиссия на катоде; последняя обусловлена не только ионной бомбардировкой, но и фотоионизацией за счет электромагнитного излучения самого разряда. Пожалуй, главным отличием от таунсендовского режима оказывается очень серьезная зависимость от пространственных координат всех характеристик