
Практика решения задач по физике. Ч.5. Квантовая физика. Евсюков В.А., Показаньева С.А
.pdf
= 1 − /(1− ) , = (1+ )/(1− ) , где = .
Первая формула определяет частоту электромагнитной волны в ′ - системе зеркала, вторая в - системе неподвижного наблюдателя для отражённой волны.
Итак, в соответствии с изложенным, частота и импульс
фотона в |
= |
|
|
|
|
|
|
|
|
|
, =а |
в |
1 −- |
/(1− ) |
и |
|||
|
′ - |
системе будут равны |
|
|
|
|
|
|
||||||||||
= |
|
|
|
= |
|
|
|
1 − |
/(1 − |
) |
|
|
|
системе |
= |
|||
(1+ )/(1− |
|
) |
|
|
= |
|
|
(1+ |
)/(1− |
|
||||||||
|
и |
= |
) |
. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В′ - системе ,в которой зеркало покоится, частота
падающего и отражённого фотонов равны , а их импульсы противоположны. Следовательно, переданный зеркалу импульс
равен |
|
|
|
|
|
|
|
|
|
|
|
, |
|
. |
|
|
|
|
|
= |
|
∙ |
|
|
|
|
= / |
|
|
|
|||||
С = 2 |
|
|
|
|
|
|
|
(1) |
|
|
|
|
|||||
точки зрения наблюдателя - системы частоты падающего |
|||||||||||||||||
и отражённого |
фотонов |
|
соответственно |
равны |
и |
, а |
|||||||||||
импульсы |
= |
|
и |
|
|
|
, |
|
имеющие |
противоположные |
|||||||
направления. При этом |
переданный зеркалу импульс равен |
|
|||||||||||||||
= + = |
|
|
1+ |
1+ |
= |
2 |
. |
|
|||||||||
|
|
|
|
1 − |
(1− ) |
|
|||||||||||
5.12. Короткий импульс лазерного излучения виртуально можно представить как отдельный испущенный фотон частоты = / , поскольку энергия аддитивная величина, а зависимость энергии кванта от частоты линейная. В процессе почти мгновенного взаимодействия импульса излучения с зеркальцем само зеркальце остаётся в покое. Вследствие этого частота и импульс фотона при отражении не изменяются. Тогда полученные зеркальцем механический импульс и кинетическая
энергия будут равны: = 2 = 2 = 2 = 2 / ,
11
= |
|
= 2 /( |
). Наличие кинетической энергии приведёт |
|
к повороту зеркальца в вертикальной плоскости относительно точки подвеса. Максимальный угол отклонения зеркальца определяется законом сохранения механической энергии:
|
|
= |
|
|
(1 −cos |
) = 2 |
|
|
sin |
|
|
|
|
|
||||||
|
|
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
= 13 |
sin |
= |
|
мг |
, |
|
sin |
= |
|
|
|
|
|||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
Для |
= 0,5 . |
= 10 |
|
|
= 10 |
см , |
максимальный угол |
|||||||||||||
|
Дж , |
о |
|
|
|
|
|
|
|
|||||||||||
отклонения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5.13.Испущенный фотон обладает гравитационной массой
ивследствие этого притягивается звездой. Удаляясь от звезды, фотон часть своей энергии затрачивает на совершение работы против гравитационной силы притяжения, первоначальная энергия фотона уменьшается. В обобщённом смысле скажем:
|
|
, где |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
= |
|
== |
|||||
работа силы идёт на приращение энергии частицы: |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
= − |
|
|
|
|
|
= |
|
|
|
|
|
− |
гравитационная |
масса |
||||||||
фотона, |
|
|
|
|
|
энергия фотона. |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|||||||||||||||
|
|
|
имеем уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Итак,= |
= |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
гравитационная |
постоянная, |
||||||||||||||||||
Здесь |
- |
масса |
звезды, |
|
|
|
|
||||||||||||||||||||
|
|
|
= |
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||
расстояние до центра звезды−. Интегрирование уравнении (1) |
|||||||||||||||||||||||||||
− |
|
= |
|
|
|
|
/ . |
При |
= |
|
∙ |
|
|
|
= |
, |
|
|
|
|
|||||||
даёт: |
|
|
|
|
и |
|
|
|
|
|
|
частота |
|
|
тогда |
||||||||||||
|
|
|
/ |
|
|
|
|
|
|
|
|
/ |
|
|
|
/ |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/ |
|
|
|
|
||||
Для |
|
= |
|
|
|
|
|
|
/ |
= . |
Приращение |
частоты фотона на |
|||||||||||||||
|
|
|
|
|
|
|
= |
− |
( |
|
− ) . |
||||||||||||||||
большом |
расстоянии от |
звезды |
|
|
|
= |
|
− = |
( |
|
|
|
− 1) |
||||||||||||||
Величина |
|
|
|
|
и, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
= − |
(1 − |
|
|
следовательно, сдвиг частоты |
|
|
|
|
|
|
||||||||||||||||
|
|
) |
отрицательный, т.е. |
в |
сторону |
||||||||||||||||||||||
|
|
|
|
/ |
< 1/ |
|
|
||||||||||||||||||||
меньших частот. Относительное смещение частоты |
|
|
|
|
|
|
|
||||||||||||||||||||
/ |
|
= −(1− |
|
/ |
|
). |
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

5.14. Коротковолновая граница сплошного рентгеновского спектра соответствует одному из вероятностных исходов, когда
кинетическая |
|
энергия ускоренного |
электрона |
|
|
|
|
|
|
при |
||||||||||||||||||||||||||
|
|
|
|
в= |
||||||||||||||||||||||||||||||||
последующем торможении |
полностью переходит |
энергию |
||||||||||||||||||||||||||||||||||
|
|
|
испущенного кванта излучения, т.е. |
|
|
|
|
|
|
, или |
||||||||||||||||||||||||||
|
= 2 / |
|
|
рентгеновской = 2 / |
|
|
|
|
|
|
переходе от |
|||||||||||||||||||||||||
|
= |
|
|
|
. |
|
|
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При= |
|
|||||||||||||||||
потенциала |
|
на |
|
|
|
|
|
|
|
|
|
|
|
|
|
трубке к потенциалу |
|
|
|
имеем : |
||||||||||||||||
′ |
|
= |
, |
′′ |
= |
|
|
|
′′ |
/ |
′ |
|
= / = ; |
|
|
|
|
|||||||||||||||||||
|
|
|
|
′ |
|
′′ |
|
|
|
|
′ |
|
|
|
|
|
||||||||||||||||||||
|
|
= |
|
− |
|
|
= |
1− |
|
|
|
|
в= 1 − |
|
∙ |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
1− |
|
|
|
. |
|
Если |
|
|
кВ, |
|
|
в пм, |
то |
|
||||||||||||||
|
= |
|
|
1 − |
|
|
|
|
|
|
|
|
|
|
= 26 |
|
|
= 1,5 |
|
|
|
|
|
|
|
|||||||||||
|
|
, |
∙ |
|
|
|
. |
Для |
|
|
|
|
|
|
|
|
|
пм, |
|
|
|
|
|
первоначальное |
||||||||||||
|
|
5.15. |
|
|
|
|
|
|
|
= 16 |
кВ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
напряжение на трубке |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
Осуществление |
|
|
зеркального |
|
отражения пучка |
|||||||||||||||||||||||||
рентгеновских лучей предполагает наличие дифракционного максимума какого-либо порядка. Дифракционные максимумы
наблюдаются при |
выполнении условия |
|
|
|
(формула |
|||
Вульфа – Брэгга). |
Здесь - угол |
скольжения, |
= 1, 2, |
… |
||||
|
2 |
sin |
= |
|
и |
|||
порядок максимума. Из формулы видно, что |
= |
, если |
||||||
= 1− |
||||||||
=. Минимальная длина волны при определённом
напряжении |
на трубке |
|
|
|
|
|
(см. |
решение 5.14). |
|||||
|
нм и |
|
2 sin |
= |
|
|
= |
∙ |
|
кВ. |
|||
Отсюда получаем: |
|
|
|
|
= 2 |
/ |
|
|
= 31 |
|
. Для |
||
|
|
|
|
|
|
|
|||||||
= 0,28 |
|
= 4,1 |
напряжение на трубке |
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||
5.16.Кинетическая энергия релятивистской частицы
= −1 , где = / . При полном превращении
−1 , где = / . При полном превращении
кинетической энергии электрона в квант рентгеновского
13 |
= |
= |
|
|
излучения имеет место равенство |
|
|
. Отсюда |
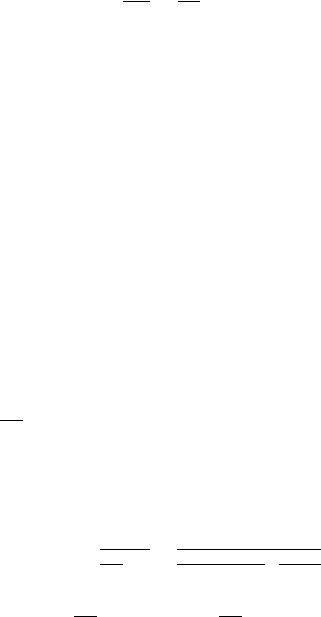
получаем |
= |
|
= |
|
/( |
|
|
− 1) . Для = 0,85 |
|
|
|||||||
|
минимальная длина волны сплошного рентгеновского спектра
=2.8 пм.
5.17.Распределение энергии в спектре тормозного рентгеновского излучения, приведённое в задаче, необходимо
скорректировать и представить в виде |
( ) = ( / |
|
−1)/ , где - |
||||||||||||||||||||
коэффициент пропорциональности. |
|
||||||||||||||||||||||
Установим связь между |
|
и |
. Связь между этими длинами |
||||||||||||||||||||
волн: излучения вытекает из условия экстремума зависимости |
= |
||||||||||||||||||||||
( ) |
⁄ = 0 |
|
|
|
|
|
− 1 ∙ |
|
= 0 − |
|
+ |
|
|
= 0 |
|||||||||
|
= 2 |
|
|
|
|
||||||||||||||||||
С |
|
= 3 |
/2 |
|
|
/3 |
|
|
|
|
|
|
|
|
|
|
(1) |
||||||
|
другой стороны, коротковолновая граница |
|
|
|
|
|
|
|
|
(2) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2), |
получим |
||||||||
|
|
|
напряжение на трубке. Приравняв (1) и = |
|
|
|
|
, |
|||||||||||||||
|
= 3 / |
При |
|
|
= 53 |
пм напряжение |
= 35 |
|
Кв. |
|
|||||||||||||
|
|
− |
|
. Для |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
5.18. |
|
|
|
|
решении |
данной |
задачи |
и |
|
|
нескольких |
||||||||||
последующих основным инструментом является уравнение
Эйнштейна для |
внешнего фотоэффекта: |
|
|
|
|
|
|
|
|
|
или |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
электрона для выбранного |
||||||||||||||
|
|
= |
+ |
|
, где - работа выхода |
|
|
|
|
|
= |
, |
+ |
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
> |
т.е. |
< |
|
||||||||
проводника. Фотоэффект имеет место, если |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
. |
Для |
|
|
|
|
|
|
|
||||||
Красная граница фотоэффекта |
= |
|
|
|
|
|
|
цинка |
|
= 3,74 |
эВ |
, |
|||||||||||
мкм. |
|
|
|
|
|||||||||||||||||||
= 2 |
∙0,66∙10 |
|
|
|
|
|
|
|
|
|
|||||||||||||
∙3∙10 /3,74 = 0,332 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Максимальная скорость вырываемых электронов с поверхности цинковой пластинки электромагнитным излучением
равна |
|
|
|
|
|
, |
∙ |
∙ ∙ |
|
∙ , |
|
= |
− = |
− |
|||||||||
|
|
, |
∙ ∙ |
∙ |
, ∙ |
||||||
= 6,6∙10 м/с.
5.19. На основании уравнения Эйнштейна имеем два
равенства |
|
= + |
|
(1), |
|
= + |
|
(2). Представим |
|
|
14

равенства (1) и (2) в виде |
|
− |
= |
|
|
|
|
|
|
(3) и |
|
|
− |
= |
|
|
|
(4), а |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
затем поделим (3) на (4): |
|
/ 1 |
|
|
|
|
|
|
|
|
|
По условию |
|
|
|
|
|
|
||||||||||
|
= |
|
|
. |
|
|
. |
|
|
|
||||||||||||||||||
|
|
, |
тогда |
|
|
/ 2− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
/ |
= |
|
|
2 / |
− = |
2 |
(2 / |
− |
) |
|
|
|
|
|||||||||||||||
Отсюда получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
|
|
= 2 |
|
|
|
− |
|
|
|
|
= |
|
|
|
|
|
− |
|
||||||||||
|
5.20. |
|
При( −1) |
|
|
|
|
|
|
|
) |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|||
|
|
|
выбывании |
|
электронов |
|
с |
поверхности |
||||||||||||||||||||
проводника действием электромагнитного излучения проводник приобретает положительный заряд, вокруг него создаётся поле кулоновских сил притяжения электронов. В отсутствие внешнего электрического поля у поверхности проводника возникает электронное облако. Через весьма малый промежуток времени после начала облучения наступает равновесие, когда число вырываемых электронов с поверхности металла становится равным числу электронов, попадающих на поверхность. При этом электронное облако будет стационарным, а потенциал уединённого проводника достигнет максимального значения . В равновесном состоянии кинетическая энергия электрона, получаемая при поглощении кванта электромагнитной энергии за вычетом работы выхода недостаточна для преодоления поля потенциальных сил притяжения, т.е. поля задерживающего
потенциала . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Итак, |
наступлению |
равновесия |
|
соответствует |
условие |
|||||||||
4,47 |
= 2 / − |
. Отсюда |
= |
|
|
∙ |
|
− |
|
. Для |
меди |
нм= |
|||
|
|
|
|
|
|
|
|
|
|||||||
эВ . |
Длина волны |
заданного |
излучения |
= 140 |
. |
||||||||||
|
|
|
|||||||||||||
Соответствующий потенциал, приобретаемый медным шариком,
|
= |
∙3∙10∙10−9 |
∙0,66∙10−15 − 4,47 = 4,4 |
|
равен |
|
8 |
|
. |
|
|
|
5.21.Электрическую составляющую излучения
представим в виде = {cos + [cos( − ) +cos( + ) ]}. Из
этого выражения видно, что данное электромагнитное излучение
15
представляет |
собой |
наложение |
волн |
с |
частотами |
, |
|
и |
|||||||||||||||
|
. |
Здесь |
|
|
|
|
|
|
|
и |
|
|
|
|
|
. |
Для лития |
работа |
|||||
+ |
= 6,0∙10 |
|
|
|
= 3,6∙ |
|
− |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
выхода |
электрона |
= 2,39 |
эВ , |
следовательно, |
красная граница |
||||||||||||||||||
фотоэффекта |
|
|
|
|
|
1/ |
. |
Частоты |
, |
|
< |
и |
только |
||||||||||
|
|
|
|
|
|
||||||||||||||||||
частота |
|
= =. |
3,62∙10 |
фотоэффект |
|
обусловлен |
|||||||||||||||||
|
|
+ |
> |
|
|
|
Поэтому |
будет |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
) |
|
|
|
|
|||
составляющей |
излучения |
|
|
|
|
|
|
|
|
. |
При |
этом |
|||||||||||
кинетическая энергия |
фотоэлектронов |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
= ( |
/2)cos( |
|
|
|
|
|
|||||||||||||
|
= ( + |
) − |
= 0,66∙10 |
(3,6+0,6) ∙10 |
− 2,39 = 0,38 |
эВ. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.22. Число фотоэлектронов, вырываемых светом в |
||||||||||||||||||||||
единицу |
времени, |
равно |
|
|
н |
|
, |
где |
|
|
н |
- |
сила фототока |
||||||||||
насыщения, |
- абсолютный= |
заряд |
электрона. |
Спектральную |
|||||||||||||||||||
|
/ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
чувствительность фотоэлемента на заданной частоте (длине
волны) определим |
величиной |
|
н |
, |
где |
|
- мощность |
||||||||||||
светового |
потока, |
падающего |
|
поверхность |
катода. |
Отсюда |
|||||||||||||
на = / |
|
|
|
|
|
|
|
||||||||||||
= |
|
/ |
. |
Мощность, |
|
|
н |
|
|
|
на |
выбивание |
одного |
||||||
|
н |
|
затрачиваемая |
||||||||||||||||
электрона |
равна |
|
равна |
|
/ |
= ( |
)/ |
|
|
. |
Энергия |
||||||||
поглощённого кванта |
|
. Квантовый выход |
|||||||||||||||||
/ |
= |
|
= |
/ |
/( |
) |
|
|
|||||||||||
|
|
|
мкм и |
= |
/( |
/ ) = (2 / )/( |
) = 2 |
. Для |
|||||||||||
фотоэлектронов |
= 4,8 |
|
/ |
|
|
= 2 / |
|
|
|
|
|||||||||
= 0,30 |
|
|
|
|
|
|
|
|
|
= 0,020 |
|
||||||||
|
|
|
|
|
|
|
мА Вт квантовый выход |
|
|
|
. |
|
|||||||
|
|
5.23. Катод фотоэлемента цезиевый, анод медный. Работа |
|||||||||||||||||
выхода электрона для цезия |
|
|
|
эВ, для меди |
|
|
|
эВ. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
освещении катода в цепи с |
||||||||
При включении фотоэлемента=и1,89 |
|
|
|
|
= 4,47 |
|
|||||||||||||
= 0,22 |
мкм в |
цепи |
появится |
фототок. |
В связи |
с |
тем, что |
||||||||||||
|
|
|
|||||||||||||||||
электроды фотоэлемента разнородные, между ними существует
внешняя контактная разность потенциалов. Поскольку |
|
, |
|
катод будет иметь положительный потенциал по |
отношению к |
||
|
< |
|
|
аноду фотоэлемента и, следовательно, поле избыточных зарядов на электродах будет тормозящим для фотоэлектронов. Контактная разность потенциалов в направлении потока фотоэлектронов − = ( − )/ . На пути от катода до
16

анода |
электрон |
теряет часть своей |
кинетической энергии на |
|||||||||||||||||||||
величину |
|
|
|
− |
|
, равную |
работе |
|
= − |
|
− |
|
= |
− |
||||||||||
тормозящего |
|
поля. |
|
Первоначальная |
кинетическая |
|
энергия |
|||||||||||||||||
|
|
( )( |
|
|
) |
|
|
|||||||||||||||||
фотоэлектрона |
|
= |
|
|
|
− |
, в конце же пути, |
т.е. у поверхности |
||||||||||||||||
анода |
|
|
|
|
|
|
|
|
|
/2 = |
|
− |
|
|
|
. |
|
|
|
|
||||
|
имеем |
равенство |
|
|
|
|
|
|
|
|
|
|||||||||||||
Итак, |
= |
|
|
|
− |
( |
− |
) = ( |
+ |
)− |
|
= |
|
−. |
Отсюда |
получаем |
||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
. Для заданных значений |
|
и |
|
наибольшая |
||||||||||||
скорость |
|
|
фотоэлектронов |
у |
поверхности |
|
анода |
равна |
||||||||||||||||
= |
2 |
|
|
|
− |
/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
∙ , |
, |
∙ |
∙ |
|
∙ ∙ |
−1,6∙10 |
∙4,47 |
/0,91∙10 |
|
= 6,4∙10 |
|
м/с. |
|
|
|||||||||
|
5.24. Сначала предположим, что оба электрода фотоэлемента |
|||||||||||||||||||||||
выполнены из одного металла (цинка). В этом случае контактная разность потенциалов равна нулю, а задерживающая разность
потенциалов V |
2 c |
|
A |
. Для цинка работа выхода А=3,74 эВ, а |
|||||||
3 |
|
e |
|
|
e |
|
|
|
|
||
задерживающий |
потенциал |
при |
заданной |
длине |
излучения |
||||||
2,62 нм V |
|
2 1,05 10 34 |
3 108 |
3,74 1 В. |
Если |
же анод |
|||||
1,6 10 19 262 10 9 |
|||||||||||
3 |
|
|
|
|
|||||||
фотоэлемента выполнен из другого металла, то эффективный задерживающий потенциал изменится за счет имеющейся внешней контактной разности потенциалов к . По условию внешний
задерживающий потенциал V / V , |
следовательно, V |
/ V |
з |
|
к |
, |
|||||
|
|
|
з |
3 |
3 |
|
|
|
|||
т.е. |
к |
V / V |
1,5 1 0,5 В. |
При |
этом контактная |
|
разность |
||||
|
з 3 |
|
|
|
|
|
|
|
|
|
|
потенциалов противоположна полярности внешнего напряжения. 5.25. Приведем обозначения размерностей и единиц
измерения в СИ для некоторых величин: а) основных механических:
длины |
[l]=[L]=L, |
[L]=м; |
массы |
[m]=[M]=M, [M]=кг; |
|
времени [t]=[T]=T, |
[T]=с; |
|
|
|
17 |

б) производных: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
скорости [v] LT 1,[v] м/c; |
|
|
|
|
|
|
|
|
|
|
|
||||||||
работы, энергии [A]=L2MT-2, [A]=Дж; |
|
|
|
|
|
|
|
|
|
||||||||||
кванта действия(постояннойПланка) |
2 2,43 10 12 |
|
( |
3 |
2 |
1 |
) 1,21. |
||||||||||||
|
|
2 1 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
4 |
||||||||
Из размерности постоянной Планка получим: |
|
|
|
|
|
|
|
|
|
||||||||||
[h] LM(LT 1) LM[v] L |
[h] |
L [ |
h |
] , |
если |
v c , где с- |
|||||||||||||
M[v] |
|
||||||||||||||||||
|
|
|
|
mc |
|
|
|
|
|
|
|
|
|
||||||
скорость света. Величина |
|
|
|
h |
, или |
|
|
|
- |
|
комптоновая |
||||||||
|
|
c |
|
mc |
|
|
mc |
|
|
|
|
|
|
||||||
длина волны частицы массой m. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5.26. Допустим, что |
|
состоялось |
событие |
|
в поглощении |
||||||||||||||
фотона свободным неподвижным электроном и попытаемся ответить на вопрос: каков результат этого события?
На основании законов сохранения энергии и импульса должны совместно выполняться два условия:
mc2 c
 p2 m2c2 (1), k p (2).
p2 m2c2 (1), k p (2).
Здесь mc2– энергия покоя электрона, p - импульс
электрона после поглощения фотона. При возведении равенства
(1) в квадрат и замене |
p2 2k2 |
2 2 /c2 на основании |
(2) |
получаем: 2 2 m2c4 |
2 mc2 |
2 2 m2c4 m 0 |
(!). |
Полученный результат не согласуется с представлением о полном поглощении свободной частицей кванта рентгеновского излучения. Действительно, рассматривая взаимодействие двух реально существующих частиц – свободного электрона и налетающего кванта – пришли к результату (!), отрицающему само существование первоначального фотона, поскольку согласно (!) 0 .
18
Итак, заключая скажем, что законы сохранения энергии и импульса исключают механизм полного поглощения кванта электромагнитного излучения свободной частицей.
5.27.Ответы на поставленные вопросы данной задачи приведены в сборнике.
5.28.На основании формулы для комптоновского смещения в данном случае имеем:
|
|
|
− |
= |
(1− |
|
|
|
|
) = 2 |
|
|
( |
|
/2). |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
′− |
1= |
(1− |
|
|
|
|
) = 2 |
2 |
|
( |
|
/2). |
|
|
|
|
|
и, |
|
|
||||||||
По условию sin( |
/2) sin300 |
|
1/2,sin( |
|
/2) sin600 |
3 /2 |
|
|
|||||||||||||||||||||||
следовательно, |
/ |
2 . Отсюда получаем: , |
|
|
|||||||||||||||||||||||||||
|
|
|
2 c sin2( 2 /2) (2 c sin2( 1 |
/2) ) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
(sin2 ( |
2 |
/2) sin2 ( |
1 |
/2)) |
|
|
1) |
|
2 с |
|
(sin |
2 |
2 |
|
sin |
2 |
1 |
) |
. |
|||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
c |
|
|
|
|
|
( |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Для 2 длина волны падающего рентгеновского излучения |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
2 2,43 10 12 |
( |
3 |
2 |
1 |
) 1,21 пм. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
2 1 |
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
5.29. |
|
Закон |
сохранения энергии |
|
для |
данной системы |
||||||||||||||||||||||||
частиц – фотон и электрон – имеет вид mc2 E . Здесьэнергия первичного фотона, - энергия рассеянного фотона, mc2 - энергия покоя электрона; E=T+mc2, где Е и Т – полная и кинетическая энергии электрона отдачи. Из закона
сохранения |
энергии |
получаем T ( ) . |
Далее, |
из |
|||||
соотношения |
2 c |
/ и |
заданного условия |
(1 ) |
|||||
находим /(1 ) |
. Итак, |
имеем: T ( |
|
) |
|
|
. |
Для |
|
|
|
||||||||
|
1 |
1 |
1,00 |
МэВ и 0,25 кинетическая энергия электрона отдачи |
|
Т=0,20 МэВ. |
|
|
19

5.30.Длина волны рассеянного фотона под углом 2
с , где с =2,43 пм – комптоновская длина волны
электрона. Соответствующая частота рассеянного фотона
2 с/ 2 c/( с ) . Для =6,0 пм частота =2,2∙1020 1/с.
Кинетическая энергия электрона отдачи
T ( ) 2 c с , см. задачу 5.29.
( c )
Для заданной длины волны фотона =6,0 пм кинетическая энергия электрона отдачи Т=60 кэВ.
5.31. Формулу c (1 cos ) , определяющую длину волны рассеянного излучения в направлении угла , представим
через частоту: |
|
|
2 c |
|
|
2 c |
|
|
2 |
(1 cos ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
В окончательном виде: |
|
|
|
|
|
|
|
|
, или |
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
(1 cos ) |
|
|
|
|
|
|
1 |
sin2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mc2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mc2 |
|
|
||||||||
|
|
|
Энергия рассеянного |
фотона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
Для |
|||||||||||||||||||||||||||||||||
|
|
|
1 |
2 |
sin2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mc2 |
2 |
|
|
|
|
|
||||||
заданных |
значений |
|
|
250 |
кэВ |
и |
|
|
=1200 |
|
|
получаем: |
||||||||||||||||||||||||||||||||||||||||||
|
mc2 |
|
0,511 |
|
|
2 |
|
,sin2 |
2 |
|
|
4 |
; энергия |
ħ |
= |
кэВ |
= 143 |
кэВ. |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
0,250 |
|
|
|
1 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
∙ |
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
/2 |
|||||||||||
|
|
|
5.32. Закон комптоновского смещения 2 c sin |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
с учетом соотношения |
|
p k 2 / |
представим через импульс |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
фотона: |
|
|
|
|
|
|
|
|
|
|
sin |
|
|
, т.е. в виде |
= |
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||||||||||||||||||
p |
|
|
|
|
p |
|
mc |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
20
