
Практика решения задач по физике. Ч.5. Квантовая физика. Евсюков В.А., Показаньева С.А
.pdfФГБОУ ВПО «Воронежский государственный технический университет»
В.А. Евсюков С.А. Показаньева Е.П. Татьянина
ПРАКТИКА РЕШЕНИЯ ЗАДАЧ ПО ФИЗИКЕ
Часть 5 КВАНТОВАЯ ФИЗИКА
Утверждено Редакционно-издательским советом университета в качестве учебного пособия
Воронеж 2013
4
УДК 535.12(075)
Евсюков В.А. Практика решения задач по физике. Ч.5. Квантовая физика: учеб. пособие / В.А. Евсюков, С.А. Показаньева, Е.П. Татьянина. Воронеж: ФГБОУ ВПО «Воронежский государственныйтехническийуниверситет», 2013. 238с.
Учебное пособие посвящено практической части общей физики для высших учебных заведений. Содержит решения большого числа задач по вопросам корпускулярно-волнового дуализма электромагнитного излучения и частиц, основ квантовой механики, физики атома, молекулы и атомного ядра. Приведены необходимые теоретические сведения и исчерпывающие пояснения по решениюрассматриваемыхзадач.
Издание соответствует требованиям Федерального государственного образовательного стандарта высшего профессионального образования по специальностям 160100.65, 160700.65, а также направлениям 151700.62, 151900.62, 221000.62, 230100.62, 230400.62, 151900.62, 131000.62, 140100.62, 221400.62, 150100.62, 150400.62, 210100.62, 221700.62, 222900.62, 223200.62.
Учебное пособие подготовлено в электронном виде в текстовом редакторе MS WORD XP, сохранено в формате pdf и содержитсяв файлеПРЗ_Ч5.pdf.
Табл. 7. Ил. 33.Библиогр.:5назв.
Рецензенты: кафедра общей физики Воронежского государственного университета (зав. кафедройд-рфиз.-мат. наук, проф.
В.В.Чернышев); д-р физ.-мат.наук, проф. Ю.Е. Калинин
©Евсюков В.А., Показаньева С.А., Татьянина Е.П., 2013
©Оформление. ФГБОУВПО«Воронежский государственный технический университет», 2013
5
ПРЕДИСЛОВИЕ
В предлагаемом учебном пособии рассматриваются задачи по вопросам корпускулярно-волнового дуализма электромагнитного излучения и микрочастиц, собственной квантовой механики, физики атома, молекулы и атомного ядра. Все задачи, о решении которых пойдет речь, заимствованы из сборника И.Е. Иродова «Задачи по общей физике», 2002 года издания. Представленные решения сохраняют нумерацию задач сборника.
Приведенные в пособии решения задач сопровождаются необходимыми рисунками, подробными и некоторыми обобщениями. Во многих случаях предварительно даются теоретические сведения по вопросам рассматриваемых задач.
Выпуск пособия адресован студентам физических и инженерно-технических специальностей. Пользование пособием может быть как систематическим, так и избирательным.
3

1. КОРПУСКУЛЯРНЫЕ СВОЙСТВА ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ
5.1. |
Энергия кванта света с длиной волны |
равна |
|
= 2 |
⁄ |
. Количество квантов света (фотонов), испускаемых в |
|
|
|
||
единицу времени источником мощности Ρ на заданной длине
волны, равно |
плотность |
потока |
. |
При |
|
изотропном |
|||||
излучении |
|
источника |
световых |
частиц на |
|||||||
|
|
|
= |
|
= |
|
|
|
|
|
|
расстоянии |
от точечного источника2 |
|
|
|
|
|
|||||
Для P=10 Вт, |
=589 |
нм |
|
/(8 |
|
. |
|
||||
и =2,0 |
м |
плотность потока |
|||||||||
фотонов |
|
= |
см с |
⁄4 |
= |
|
|
) |
|
|
|
Установим связь между плотностью потока фотонов и их |
|||||||||||
|
= 6∙10 1/ |
|
∙ . |
|
|
|
|
|
|
|
|
концентрацией n. Количество фотонов, поступающих за время
|
|
|
|
|
|
|
|
элемента |
сферического слоя площадью |
|
|
и |
|||||||||||||||||||
|
|
в объём |
|
|
|
|
|||||||||||||||||||||||||
толщиной |
|
, равно |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||||
|
|
|
|
|
= ∙ = ∙ ⁄ = |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Следовательно, концентрация фотонов |
⁄8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Отсюда |
|
|
= |
⁄ |
= ⁄ = |
|
|
|
|
|
|
|
|
|
|
|
(1). |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
получаем |
|
выражение |
для |
|
расстояния |
|
|
|
по |
|||||||||||||||
известному значению концентрации фотонов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Для |
= 100 |
= |
⁄(8м |
. |
) |
= |
⁄2 |
⁄2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
см |
|
|
|
|
|
|
|
|
где |
||||||||||||||||||||||
|
|
|
|
, = 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
5.2. Модуль импульса фотона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
= |
⁄ |
|
|
|
|
|
|
|
|
|
|
виде |
= |
|
|
. Поскольку |
||||||||||||||
|
|
|
|
-волновое число. В векторном |
|
= |
|
|
= |
|
|||||||||||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
= , |
|
|
||||||||||||||||
|
= 2 / |
, модуль импульса фотона можно представить |
|
в виде |
|||||||||||||||||||||||||||
|
. Постоянная Планка |
= 1,055∙10 |
|
|
Дж |
∙ |
с |
= 0,659∙ |
|||||||||||||||||||||||
|
= 2 / |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
эВ |
|
эВ. |
|
|
|
|
|
|
|
|
|
|
[ ] = [ ]⁄[ |
|
] = |
|
|
|
∙ |
⁄ |
|
= |
|||||||||
|
м с |
|
|
|
|
|
импульса |
|
эВ |
|
|||||||||||||||||||||
10 |
Размерность |
|
|
|
|
|
|
|
|
|
|
|
|
с м |
|
||||||||||||||||
|
|
⁄( |
⁄ ). |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

Импульс фотона даже в единицах эВ |
с м весьма малая |
||||||||||
величина. |
В связи |
с |
этим импульсу |
фотона |
сопоставляют |
||||||
|
|
∙ ⁄ |
|
|
|||||||
величину |
|
( |
|
– скорость света) измеряемую в эВ. Тогда |
|||||||
|
импульс |
|
|
|
|
|
|
|
эВ |
||
реальный |
= |
|
|
|
с с и размерность |
|
|
с |
, где с – не |
||
единица измерения |
времени – секунда, а скорость света. |
||||||||||
|
= |
/ |
|
|
[ ] = |
|
= 0,25 мкм |
||||
Для фотонов с длинами волн |
= 0,50 мкм, |
|
|||||||||
и= 4,0 пм соответствующие импульсы в единицах эВ/с равны:
|
= |
с |
= |
|
∙ ∙ |
∙ , ∙ |
|
∙ |
эВ |
= 2,48 |
эВ |
|
|
|
|
|
|
|
с |
|
с |
|
|||||||||
|
|
эВ |
, |
∙ |
|
|
|
МэВ, . |
|
||||||
5.3. |
= 2 |
5 |
|
, |
= 1,25∙10 |
|
= 0,31 |
|
|
|
|
= |
|||
с |
|
|
с |
||||||||||||
|
Из |
релятивистского |
соотношения |
+ |
|||||||||||
|
|
|
|
|
|
||||||||||
=+ выражаем импульс электрона и равняем его
импульсу фотона 2 ⁄ : ( |
+ |
) |
= |
+ |
)⁄ |
|
|
Далее: |
||||||||
|
+2 |
= |
|
|
|
= |
|
|
( |
|
+2 |
|
. . |
Для |
||
|
|
|
|
|
|
|||||||||||
= 2 /МэВдлина |
|
|
= |
= |
( |
м |
) |
|
пм. |
|||||||
|
= 0,30 |
|
волны фотона |
|
|
|
|
|
|
|
|
|||||
|
= |
, ( , |
∙∙,∙ |
) |
/ , |
∙ |
= 2,0∙10 |
|
= 2,0 |
|
||||||
5.4.Импульсы по модулю электрона и фотона
соответственно |
равны |
|
э |
|
|
|
|
|
и |
|
|
. По |
|||||||
|
|
|
|
|
|
|
|
|
равенство |
|
|
|
|
|
|
|
|||
условию |
|
э |
|
|
. Отсюда |
1 − |
⁄ |
|
= 2 ⁄ |
, |
|||||||||
|
|
|
|
|
= |
⁄ |
|
||||||||||||
|
|
|
|
выражаем скорость электрона: |
⁄ |
|
= 2 ⁄ |
|
|||||||||||
из которого= |
|
|
|
|
|
|
|
|
⁄ |
1 − |
|
|
|||||||
|
= |
4 |
1 − |
|
|
( |
|
|
+4 ) = 4 |
||||||||||
|
|
|
|
||||||||||||||||
= |
|
|
пм |
|
= |
|
|
|
|
|
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
( |
⁄ |
) |
|
|
|
|
|
|||||||
Для |
= 5,0 |
|
|
скорость электрона |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5

=  = 0,43
= 0,43
1+( |
0,91∙10 |
∙3∙10 |
∙5,0∙10 |
) |
||
2 |
|
м с |
|
|
||
|
∙1,05∙10 |
|
|
|||
5.5. Сначала= 1,3∙10 |
/ . |
|
импульса и энергии за |
|||
|
выразим |
потоки |
||||
единицу времени через нормальную площадку для фотонов
одной частоты . |
Импульс фотона |
|
|
|
|
|
|
|
|
|
|
|
, где |
|
||||||||||
Импульс, |
|
|
||||||||||||||||||||||
- энергия |
фотона. |
Отсюда |
|
=. |
переносимый |
|||||||||||||||||||
|
|
= |
= |
|
= |
|
|
|
||||||||||||||||
световым |
потоком |
за |
единицу |
времени через |
|
нормальную |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
площадку площади F, будет определяться суммой импульсов |
||||||||||||||||||||||||
фотонов, |
находящихся |
в |
объёме |
поток |
, т.е. |
|
|
через |
|
|
||||||||||||||
|
|
|
|
|
|
|
(1). При |
этом |
энергии |
ту же |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
⁄ |
= |
|
= |
|
площадку Φ |
|
|
|
(2). Сравнивая |
(1) и |
(2), |
получаем |
|||||||||||||||||
= ( ⁄ ) |
=э |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Φ |
э |
|
(3). Суммируя (или интегрируя) по всему |
спектру |
||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
= |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
частот светового потока, получим то же соотношение (3). |
|
|
|
|||||||||||||||||||||
= |
|
|
⁄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.6. Давление электромагнитной волны при нормальном |
|||||||||||||||||||||
падении на плоскую поверхность тела равно |
= |
- |
|
|
|
|
, где |
|||||||||||||||||
|
|
|
|
- средняя |
плотность энергии волны, |
коэффициент |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1+ ) < |
|
> |
|
||||||
отражения. Плотность энергии в импульсе лазерного излучения |
|||||||||||||||||
< |
> |
⁄( |
) = |
/( |
) |
|
|
|
|
|
|
|
|
|
|||
< |
>= |
, |
где |
- |
пространственная |
длина |
|||||||||||
импульса, |
|
|
= |
|
⁄4 |
- площадь сечения пучка, - длительность |
|||||||||||
импульса. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для |
Давление |
светового |
|
импульса |
на стенку |
в |
течение |
||||||||||
|
|
Дж |
|
|
|
мс |
|
|
|
= 4(1+ |
) |
⁄МПа . |
|||||
промежутка времени его действия равно |
|
= 5,0 |
= |
||||||||||||||
|
= 10 |
|
|
, |
= 0,13 |
|
, |
= 0,5 ; |
давление |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
=50 атм.
5.7.Электромагнитное поле (волна) обладает импульсом. Для характеристики динамического воздействия электромагнитной волны на вещество вводят понятие плотности импульса
, определяемой импульсом электромагнитного поля в единице
6

объёма. Плотность импульса находится в определённой связи с другими характеристиками электромагнитной волны. Приводя эти соотношения, будем полагать, что электромагнитная волна распространяется в вакууме.
Плотность импульса волны в произвольной точке и
произвольный момент времени определим так: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
= ( |
|
) |
|
|
|
|
∙ |
|
|
|
= |
|
|
|
|
|
|
∙ |
|
|
|
|
= |
|
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
едс |
|
|
с |
|
|
с |
|
|
|
с |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
||||||||||||||||||||||||||||||||
Здесь |
ед -релятивистская |
|
|
масса |
|
единицы |
объёма |
поля с |
||||||||||||||||||||||||||||||||||||||||||||||||||||
объёмной( )плотностью энергии |
|
|
|
w |
|
|
в |
точке |
( |
, |
) |
; |
|
- волновой |
||||||||||||||||||||||||||||||||||||||||||||||
вектор, |
⁄ |
|
|
|
- |
|
|
|
орт |
|
|
|
|
|
|
направления |
|
|
|
распространения |
||||||||||||||||||||||||||||||||||||||||
электромагнитной |
волны. Среднее по времени значение |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
взаимную |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
, |
(2) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Учитывая |
|
|
|
|
ориентацию векторов |
|
|
|
и |
|||||||||||||||||||||||||||||||||||||||||||||||||||
соотношение |
|
|
|
|
|
|
|
|
< |
|
|
|
|
>= |
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
|
|
для плотности |
энергии |
||||||||||||||||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
, ( |
|
|
= |
|
|
|
|
|
= |
1) |
|
|||||||||||||||||||||||||||||||||||||
волны получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
. |
|
(3) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
энергии (вектор Пойтинга) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
Плотность потока= |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= = |
|
|
|
∙ |
|
=E |
|
|
|
|
|
|
|
|
|
|
∙ |
|
= |
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
∙ |
|
= |
|
|
|
∙ |
|
= |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
имеем |
|
|
|
|
|
т е |
|
|
|
|
|
|
|
|
|
|
|
⁄ |
|
|
|
|
|
|
= |
⁄ |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
. |
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Отсюда с учётом (2) |
= |
|
|
|
|
∙ |
, |
|
|
|
. |
|
|
, а также∙ |
. |
|
|
|
|
по |
. |
|
(5) |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Практически |
значимыми |
|
являются |
|
средние |
времени |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
величины |
< >= |
|
< |
|
|
|
|
|
> |
|
, < >= |
|
|
|
|
∙ |
|
. |
|
|
|
|
|
(6) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
В последующих действиях для упрощения символики угловые скобки средних величин опустим.
Для временного́ импульса электромагнитной волны в пространстве объёмом V динамический импульс
7
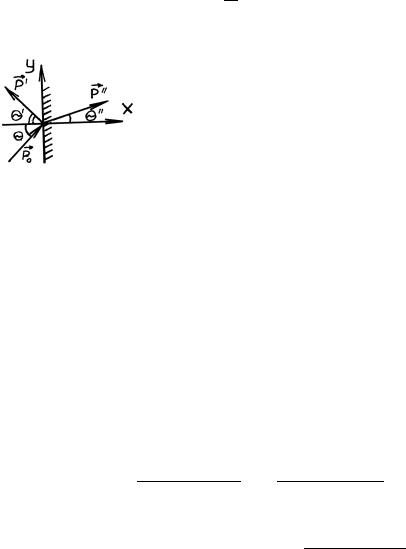
|
|
|
|
|
|
|
|
|
= |
|
= |
|
|
|
|
∙ |
|
= |
|
∙ |
|
, |
|
|
|
|
|
|
|
|
|
(7) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где - энергия цуга волны. Если импульс падающей волны |
||||||||||||||||||||||||||||||||||||||
обозначить через |
|
, то |
|
|
|
|
|
|
|
. Из соотношения (7) видно, что |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
векторы |
|
и |
|
имеют |
одно |
направление. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
= |
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
и ′′ |
|||||||||||
|
|
|
|
|
|
|
|
|
Теперь |
|
|
|
найдём |
|
импульсы |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
отражённой |
|
|
и проходящей волн. Для |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
составляющих |
|
векторов |
У, |
′ |
и |
|
′′ |
|
вдоль |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
координатных осей Х и |
(см. рис.) по с |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
закону |
|
|
сохранения |
|
импульса |
|
|
можем |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
написать: |
|
|
− |
|
|
|
|
|
|
|
, |
|
= |
; |
|
|
|
|
|
|
|||||||||
|
|
а) для х-составляющих |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
|
|
|
′′ |
|
′ |
|
|
|
|
′ |
|
|
|
|
|
|
||||||||
|
|
б) для у- |
составляющих |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
= |
= |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Из этих равенств следует: |
|
|
′ |
|
|
|
|
|
|
′′ |
|
|
|
′′. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
|
|
|
′′ |
= ( |
|
+ |
′ |
) |
|
, |
|
|
|
|
|
(8) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
|
|
|
′′ |
|
′ |
|
|
|
|
|
|
(9) |
||||||||||||
При возведении в квадрат |
равенств (8) и (9) и последующем их |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
− |
= ( |
|
|
− |
|
) |
|
. |
|
|
|
). |
|
|
= |
|||||||||||||||||||
сложении |
получим |
′′ |
= ( |
|
|
|
|
|
′ |
) |
|
|
|
|
|
|
|
+( |
++ |
′ |
|
|
||||||||||||||||
2 |
|
2 |
|
|
|
′ |
( |
2 |
|
|
2 |
) = |
|
|
2 |
|
|
|
′ |
2 |
|
|
|
|
|
′ |
|
|
|
|
|
|
||||||
0 + |
′ |
+2 |
|
|
|
− |
|
|
0 + |
|
|
|
+ +2 0 |
|
2 |
|
|
|
|
|
||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(10) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Отношение энергий для отражённой и падающей волн есть |
|||||||||||||||||||||||||||||||||||||
коэффициент отражения. Поскольку импульс |
|
|
, |
то |
′ |
′′ |
|
|||||||||||||||||||||||||||||||
и, следовательно, равенство (10) |
|
можно |
представить как |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
~ |
|
|
|
|
|
= |
|
||||||||||||||||||||||||||||
|
(1+ |
|
+2′′= |
2 |
. Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||||||
Величину |
(11) |
|
|
1+ |
+2 |
|
|
|
2 |
|
|
= |
|
|
|
1+ |
+2 |
|
2 . |
|
величину |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
можно |
толковать |
|
как |
|
|
абсолютную |
|
|||||||||||||||||||||||
импульса р, переданного телу электромагнитной волной
некоторой протяжённости. Итак, = ( ⁄ ) 1+ +2 2 .
8
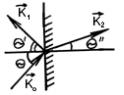
5.8. Рассматриваем плоскую монохроматическую световую волну как поток световых квантов, энергия и импульс
которых |
= |
и |
= |
. |
На |
плоскую |
поверхность тела единичной |
|
площади за 1с |
||||
падает |
|
|
квантов света (фотонов), где n – объёмная |
|||
фотонов (концентрация), |
- угол падения волны (см. |
|||||
плотность= |
cos |
|
|
|
|
|
рис.). При этом на данную площадку падает энергия = ∙ =
cos и соответствующий механический импульс
|
= |
∙ = |
|
cos |
∙ = |
cos ∙ |
|
|
|
|
|
||||||
где |
− |
орт |
волнового вектора . |
|
, |
|||
Давление |
света |
|
, как |
действие |
нормальной силы на |
|||
единичную площадку при полном его поглощении равно
изменению |
|
импульса |
|
= |
|
|
= . |
При, |
наличиит.е. |
|||||
= cos = ( |
cos |
)cos |
|
|
cos |
|
|
|
|
|||||
отражения |
волны |
давление |
|
) |
согласно |
закону сохранения |
||||||||
Концентрацию |
|
= (1+ |
= (1+ |
) |
cos |
(1). |
||||||||
импульса будет равно |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
фотонов в падающей волне найдём по |
||||||||||||
заданной плотности потока энергии (интенсивности): |
(3) |
|||||||||||||
=< |
>= ( |
) |
= |
с |
|
= |
|
⁄( |
). |
|
||||
Подставляя (2) в (1), получим |
|
= (1+ |
) |
|
|
cos . |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Вобычной символике, давление = .
5.9.Результирующая сила светового давления, испытываемая шаром, равна произведению давления света и
площади поперечного большого сечения шара, т.е. |
|
, |
|||||||
где |
- радиус шара. |
Поверхность шара является |
=идеально∙ |
||||||
отражающей, |
= |
|
. Согласно формуле (3) задачи 5.8. при |
|
|||||
|
|
= |
|
|
|
|
|
|
|
получаем |
|
= 1 |
|
|
. |
|
= 0 |
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
9 |
|
|
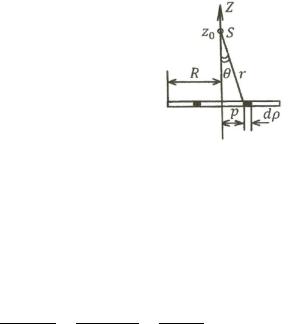
5.10.Здесь также воспользуемся
формулой (3) задачи |
5.8., |
учитывая |
что |
||
В= 1 |
: давление света |
= (2 |
⁄ )cos |
. |
|
|
|
|
|
||
рассматриваемом случае |
интенсивность |
||||
светового потока |
|
|
, где |
- |
|
|
источника света, |
а - |
|||
мощность точечного= |
⁄(4 |
) |
|
|
|
расстояние до выбранной точки заданной поверхности.
Пространственное положение источника света и круглой пластинки показано на рисунке. Сила давления на кольцевой
элемент, |
поверхности круглой пластинки |
как= ∙ |
= (2 ⁄ )cos |
и∙ |
|||||||||||||||
где |
- радиус |
кольца. Так |
|||||||||||||||||
2 |
|
|
, то |
|
|
|
|
|
|
|
|
|
|
cos. |
= / |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
+ |
= |
|
= ( |
) |
|
|||||||||||||
= |
|
|
|
|
|
|
|
|
|
||||||||||
Результирующая сила светового давления на пластинку равна |
|
||||||||||||||||||
|
|
|
= |
|
∫ |
( |
) |
= |
( |
) |
= |
( |
) |
. |
|
||||
|
|
|
|
|
|||||||||||||||
5.11. Читателю имеет смысл сначала ознакомиться с решением задачи 3.280, в котором установлена связь между частотами падающей электромагнитной волны и отражённой от движущегося зеркала. С квантовой точки зрения электромагнитная волна рассматривается как потом фотонов с определённым их пространственно-временным распределением.
В данной задаче объектом рассмотрения является отдельный фотон, характеризуемый определёнными величинами: частотой
энергией |
= |
и |
импульсом |
= |
. Частоту кванта |
|
частоте |
||||
электромагнитного, |
поля |
равняют |
соответствующей |
||
электромагнитной волны. В связи с этим, релятивистский закон преобразования частоты волны и отдельного фотона при переходе из одной системы отсчёта в другую один и тот же.
Приведём формулы (1) и (3) задачи 3.280:
10
