2836.Труды IX Международной (XX Всероссийской) конференции по автоматизирова
..pdfУЖД участвует в формировании желаемых динамиче- |
|
a(t, x) = − |
Rя |
ω(1) |
|
Rя |
Mc − |
(сФн ) |
2 |
|
ω− |
1 |
|
|
|||||||||||||||||||||||||||||||||
|
– |
|
|
|
Mc |
(1) ; |
|||||||||||||||||||||||||||||||||||||||||
ских свойств системы управления. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
JLя |
|
|
|
|
J |
||||||||||||||||||||||||||||||||||||
|
Эффективность стабилизации нестационарных ОУ |
|
|
Lя |
|
|
|
|
|
|
|
|
JLя |
|
|
|
|
|
(3) |
||||||||||||||||||||||||||||
с обеспечением желаемых статических и динамиче- |
|
|
|
|
|
|
b(t,x)= |
сФн |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
ских свойств подтверждается путем применения мето- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
дов больших коэффициентов и локализации для син- |
|
|
|
|
|
|
|
|
|
|
JLя |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
теза систем управления электроприводами постоянно- |
|
II. МЕТОД БОЛЬШИХ КОЭФФИЦИЕНТОВ |
|
||||||||||||||||||||||||||||||||||||||||||||
го тока [1]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В основе метода лежит принцип «глубокой» обрат- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
I. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ |
|
ной связи, посредством которого замкнутая система де- |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ОБЪЕКТА УПРАВЛЕНИЯ |
|
|
|
лится как минимум на две подсистемы с различными |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
темпами – быстрыми и медленными. Подсистема с бы- |
||||||||||||||||||||||||||||||||||||||
|
Общие положения рассматриваемых методов будут |
||||||||||||||||||||||||||||||||||||||||||||||
|
стрыми движениями называется контуром быстрых |
||||||||||||||||||||||||||||||||||||||||||||||
относиться к одноканальным непрерывным ОУ, мате- |
движений (КБД), которая подавляет (локализует) нели- |
||||||||||||||||||||||||||||||||||||||||||||||
матическое описание которых должно быть представ- |
нейность и нестационарность ОУ вместе с внешними |
||||||||||||||||||||||||||||||||||||||||||||||
лено в канонической форме записи: |
|
|
|
возмущениями. Подсистема с медленными движениями |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
называется контуром медленных движений (КМД), ко- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
x(n) = a(t, x) + b(t, x)u , |
|
(1) |
торая близка к желаемым процессам и обладает малой |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чувствительностью к изменениям параметров объекта |
||||||||||||||||||||||||
|
|
d |
n |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
управления. Самым оптимальным вариантом является |
||||||||||||||||||||||||
где |
x(n) = |
|
– |
старшая |
|
производная |
регулируемой |
система автоматического управления (САУ) с тремя |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
dtn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
темпами движения – быстрыми, медленными и сверхбы- |
||||||||||||||||||||||||||||
переменной; |
x = |
|
|
(1) |
, x |
(2) |
, , x |
(n |
−1) T |
– |
вектор |
кано- |
стрыми. Подсистема со сверхбыстрым темпом называет- |
||||||||||||||||||||||||||||||||||
x, x |
|
|
|
|
|
|
ся дифференцирующим фильтром (ДФ) и применяется |
||||||||||||||||||||||||||||||||||||||||
нических для методов управления движениями на ин- |
|||||||||||||||||||||||||||||||||||||||||||||||
для вычисления оценок неизмеряемых производных вы- |
|||||||||||||||||||||||||||||||||||||||||||||||
вариантных |
|
многообразиях |
координат состояния; |
ходной регулируемой переменной и обеспечения необ- |
|||||||||||||||||||||||||||||||||||||||||||
a(t, x) – функция-множитель, которая учитывает как |
ходимой помехозащищенности [1]. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
параметрические, |
так |
и |
возмущающие |
воздействия; |
Исходя из желаемых показателей качества переход- |
||||||||||||||||||||||||||||||||||||||||||
b(t, x) – функция-множитель, которая учитывает толь- |
ных процессов по задающему воздействию v(t) |
выбира- |
|||||||||||||||||||||||||||||||||||||||||||||
ко |
параметрические |
воздействия; |
u |
– |
управляющее |
ем УЖД (n–1)-го порядка, котороеимеетследующийвид: |
|||||||||||||||||||||||||||||||||||||||||
воздействие. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
В качестве ОУ были выбраны двигатель постоянно- |
|
|
|
|
|
|
F(v, x) = 0, |
|
|
|
|
|
|
|
|
|
|
(4) |
||||||||||||||||||||||||||||
го тока (ДПТ) серии 2П. Было принято, что сопротив- |
|
|
|
|
|
ω(1) = (v – ω) |
Ω |
|
, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
ление якоря изменяется под действием температурного |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ж |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
дрейфа, следовательно, ДПТ можно считать нестацио- |
где Ωж – среднегеометрический корень характеристи- |
||||||||||||||||||||||||||||||||||||||||||||||
нарным объектом управления, математическое описа- |
|||||||||||||||||||||||||||||||||||||||||||||||
ние которого представлено в следующем виде: |
|
ческого полинома УЖД; v – некоторое задающее воз- |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
diя = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
действие. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
(U |
|
− i |
R |
− e |
), |
|
|
Составляем |
|
пропорциональный |
закон |
управления |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Lя |
|
|
я |
я |
|
я |
я |
|
|
|
(ЗУ), выражение которого имеет вид |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||
|
|
|
|
|
dω |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
u = μ |
−1 |
|
|
|
μ |
−1 |
(F |
0 |
(v, |
) |
(1) |
), |
(5) |
|||||||||||||
|
|
|
|
|
= |
|
(M − Mc ), |
|
|
|
|
|
|
F(v, ω) = |
|
|
|
ω |
|
− ω |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где μ – малый параметр; |
μ−1 – большой коэффициент, |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= cФнω, |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
eя |
|
|
|
|
|
|
который обеспечивает разделение темпов движения |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
M = cФнiя , |
|
|
|
|
|
процессов КБД и КМД. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассчитываем дифференцирующий фильтр n-го по- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
где |
iя – ток якорной цепи двигателя; |
Uя |
– напряжение |
рядка, дифференциальное уравнение которого имеет |
|||||||||||||||||||||||||||||||||||||||||||
следующий вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
якорной цепи двигателя; eя |
– ЭДС якорной цепи двигате- |
|
|
|
2 |
ˆ (2) |
|
|
|
|
ˆ (1) |
+ |
ˆ |
|
= ω, |
|
|
(6) |
|||||||||||||||||||||||||||||
ля; |
L – индуктивность якорной цепи двигателя; J |
– мо- |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
Tф |
ω |
+ A1фTфω |
ω |
|
|
||||||||||||||||||||||||||||||||||||||||
|
я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
мент инерции двигателя; ω – скорость двигателя; |
M – |
где |
A1ф – коэффициент характеристического полинома |
||||||||||||||||||||||||||||||||||||||||||||
динамический момент двигателя; Mc – статический мо- |
|||||||||||||||||||||||||||||||||||||||||||||||
мент двигателя; c – конструктивная постоянная; Фн |
– но- |
при |
стандартной |
линейной |
форме |
Баттерворта; Tф – |
|||||||||||||||||||||||||||||||||||||||||
минальныймагнитныйпотокдвигателя[2]. |
|
|
постоянная времени ДФ, которую находят из условия |
||||||||||||||||||||||||||||||||||||||||||||
|
После некоторых преобразований математической |
разделения темпов быстрых и сверхбыстрых движений. |
|||||||||||||||||||||||||||||||||||||||||||||
модели ДПТ можно выделить функции-множители |
Укрупненная структурная схема системы управле- |
||||||||||||||||||||||||||||||||||||||||||||||
a(t, x) и b(t, x) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
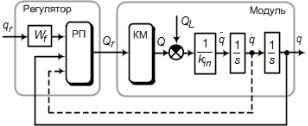
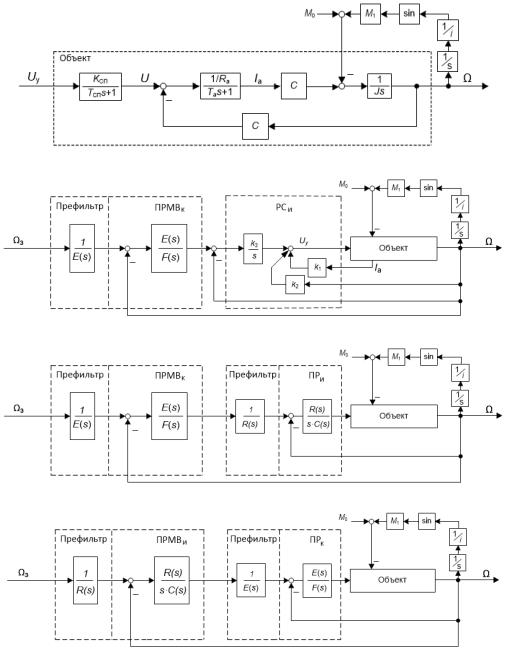
ния представлена на рис. 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
____________________________________________________________________________________________________________________________
IX Международная (XX Всероссийская) конференция по автоматизированному электроприводу АЭП-2016
- 171 -
системы регулирования скорости с РСи и ПРи в структу- |
Применение принципа последовательной коррекции |
рах на рисунке, б, в может обеспечить снижение чувст- |
при использовании РСи в составе внутреннего контура |
вительности ЭМС к воздействию помех и влиянию запаз- |
управления незначительно повышает степень сложно- |
дывания сигналов СП. В этом случае при синтезе внешне- |
сти регуляторов, но сопровождается погрешностями |
го ПР с МВк по уравнению (5) умеренно (в 2–2,5 раза) |
аппроксимации внутренней подсистемы звеном низкого |
ускоренная внутренняя подсистема аппроксимируется |
порядка. Снизить погрешности аппроксимация позво- |
апериодическим звеном 1-го порядка. |
ляет представление внутренней подсистемы апериоди- |
Полученные значения коэффициентов ОС, выраже- |
ческим звеном 2-го порядка. Полученные значения ко- |
ния и параметры полиномов ПФ регуляторов для П |
эффициентов ОС, выражения и параметры полиномов |
(ПРМВк-РСи), приведены в третьей строке табл. 1. |
ПФ регуляторов для данной ЭМС, обозначенной как П2 |
При синтезе внутренней подсистемы с использовани- |
(ПРМВк-РСи), приведены в четвертой строке табл. 1. |
ем ПРи общий порядок звеньев регуляторов возрастает |
Из их анализа следует, что степень сложности регуля- |
до 8, что делает синтез такой ЭМС нецелесообразным. |
торов в этом случае существенно возрастает. |
а
б
в
г
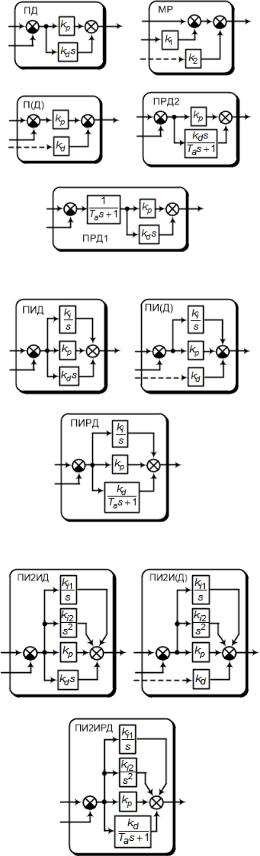
Рис. Структурные схемы объекта управления и различных вариантов ЭМС
____________________________________________________________________________________________________________________________
IX Международная (XX Всероссийская) конференция по автоматизированному электроприводу АЭП-2016
- 176 -