
2629
.pdf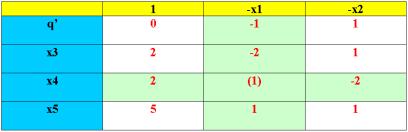
Здесь выделены свободные члены. Построим таблицу (матрицу) коэффициентов вида (рис. 3.4).
Рис. 3.4. Матрица коэффициентов системы 1.5
Выделенные красным цифры – это коэффициенты преобразованной системы уравнений.
Проверяем, не найдено ли оптимальное решение. Поскольку в строке q’ коэффициент при х1 отрицательный, то оптимальное решение не найдено и переменную х1 следует сделать базисной.
Если отрицательными окажутся несколько свободных переменных, то в базисную можно переводить любую.
Определим, какую из базисных переменных сделать свободной. Такую, для которой коэффициент в столбце х1 положительный и отношение к этому положительному коэффициенту минимальное. Это х4 (2/1<5/1).
Этот коэффициент выделен круглыми скобками (1) и называется генеральным. Заполнение нижних коэффициентов таблицы (см. рис. 3.4) выполняется по следующим правилам:
1.В клетку на пересечении отмеченных строки и столбца записываем 1/
2.В клетках отмеченной строки записываем верхние ко-
эффициенты, умноженные на 1/ .
3. В клетках отмеченного столбца записываем коэффициенты, умноженные на –1/ .
61
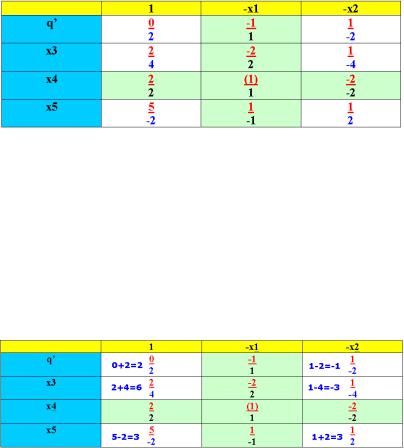
4. В остальных клетках записываем произведение уже полученных нижних коэффициентов из столбца х1 на верхний коэффициент соответствующего для данной клетки столбца на пересечении которых стоит.
Получаем нижние значения таблицы (отмечены чёрным цветом) (рис. 3.5).
Рис. 3.5. Матрица коэффициентов с нижними значениями
Строим следующую таблицу (рис. 3.6), в которой х1 становится базисной переменной, а х4 – свободной. Верхние числа этой таблицы получаются так:
1.Строка и столбец, соответствующие новым свободной
ибазисной переменным, заполняются нижними коэффициентами отмеченной строки и столбца.
2.В остальных клетках записываются суммы коэффициентов из предыдущей таблицы (рис. 3.7):
Рис. 3.6. Заполнение таблицы, в которой х1 становится базисной переменной, а х4 – свободной
62
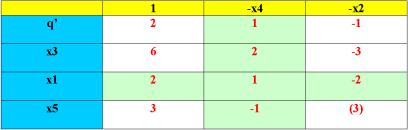
Рис. 3.7. Таблица коэффициентов для х1 – базисная, х4 – свободная
Поскольку в новой таблице (см. рис. 3.7) в строке q’ коэффициент при х2 отрицательный, то оптимальное решение не найдено, и переменную х2 следует сделать базисной. Здесь генеральный коэффициент = 3 (всего один коэффициент в столбце х2 больше нуля – он выделен круглыми скобками).
Получаем новые нижние коэффициенты. Заполнение нижних коэффициентов выполняется по следующим правилам:
1.В клетку на пересечении отмеченных строки и столбца записываем 1/ = 1/3;
2.В клетках отмеченной строки записываем верхние ко-
эффициенты, умноженные на 1/ = 1/3;
3.В клетках отмеченного столбца записываем коэффициенты, умноженные на – 1/ ;
4.В остальных клетках записываем произведение уже полученных нижних коэффициентов из столбца х2 на верхний ко-
эффициент соответствующего для данной клетки столбца, на пересечении которых стоит.
Так, для столбца «1» (рис. 3.8) имеем: Х5:3 – верхний коэффициент «3» выделенной строки Х5 умножаем на 1/3 = 1.
Х1:3*2/3 = 2. Х3:3*1 = 3. q’:3* 1/3 = 1.
Подробно процесс заполнения столбца 1 показан на рис. 3.9–3.12:
63
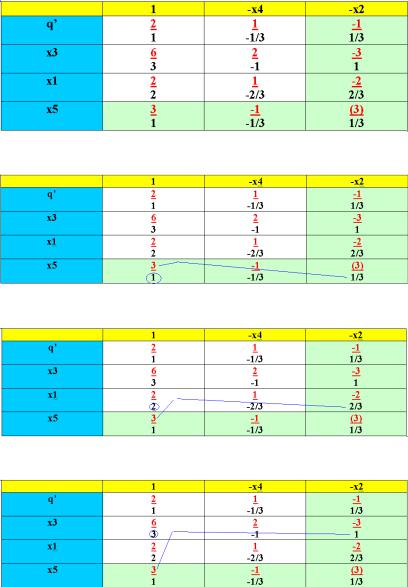
Рис. 3.8. Таблица коэффициентов для х2 – базисная
Рис. 3.9. Заполнение клетки х5,1
Рис. 3.10. Заполнение клетки х1,1
Рис. 3.11. Заполнение клетки х3,1
64
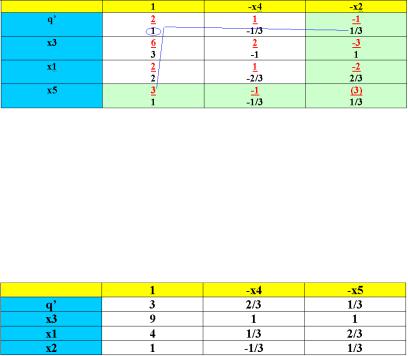
Рис. 3.12. Заполнение клетки q’,1
Переходим к базису х3, х2, х1:
1.Строка и столбец, соответствующие новым свободной
ибазисной переменным, заполняются нижними коэффициентами отмеченной строки и столбца.
2.В остальных клетках записываются суммы коэффициентов из таблицы (см. рис. 3.8–3.12), получаем рис. 3.13.
Рис. 3.13. Результат решения задачи линейного программирования (3.1)
В строке q’ все коэффициенты положительны, значит, оптимальное решение достигнуто, и оно записано в столбце свободных членов:
x1
x2
x3
x4
x5q '
4;
1;
9;
0;
0;
3.
65

Таким образом, табличный симплекс метод (алгоритм) – это формализация вышеописанных процедур решения уравнений путём выражения одних переменных через другие, и он был реализован на ЭВМ ещё на рубеже 40–50-х гг. ХХ в.
3.5.Решение задачи линейного программирования
вСКМ «Маткад» [22]
Получим решение той же задачи – системы (3.2) в системе компьютерного моделирования СКМ «Маткад» (рис. 3.14).
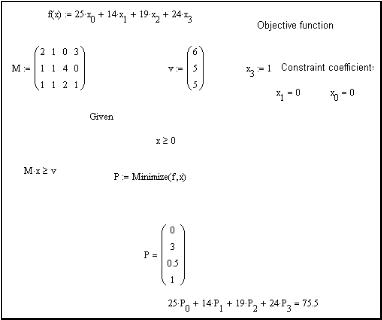
Рис. 3.14. Решение задачи линейного программирования в СКМ «Маткад»
На рис. 3.14 сверху вниз указаны целевая (минимизируемая) функция f(x), матрица М коэффициентов при неизвестных системы уравнений (3.2), причём нумерация матрицы идёт с нуля, вектор v значений правой части системы (3.1), опорное зна-
66
чение одной из переменных (х5), причём без указания таких значений одной или нескольких переменных решение не может быть найдено.
Далее идёт блок Дано (Given), в котором указаны ограничения – равенство, поскольку мы ввели дополнительные переменные х4, х5 в системе (3.2) по отношению к системе (3.1). Указано, что переменные положительны. Минимизация реализуется опцией Minimize (f, x).
При этом вводится дополнительно строка Р для того, чтобы получить значение функции, в данном случае оно равно –3.
3.6. Двойственная задача линейного программирования
Рассмотрим двойственную задачу линейного программирования на примере [19].
Пусть для обеспечения трёх параметров эффективности системы управления х1, х2, х3 необходимы четыре вида ресурсов (может быть, это некие допустимые статьи расходов).
Ресурсы ограничены (деньги на расходы). Системный эффект от частных параметров различен, но линеен. Необходимо максимизировать системный показатель безопасности.
Вид |
|
Расход на единицу |
|
Запасы |
||
ресурса |
|
частного показателя |
|
ресурсов |
||
|
Т1 |
|
Т2 |
|
Т3 |
|
S1 |
2 |
|
1 |
|
1 |
25 |
S2 |
1 |
|
1 |
|
1 |
14 |
S3 |
0 |
|
4 |
|
2 |
19 |
S4 |
3 |
|
0 |
|
1 |
24 |
Системный эффект |
6 |
|
5 |
|
5 |
|
безопасности |
|
|
|
|
|
|
Рис. 3.15. Пример задачи обеспечения трёх параметров безопасности
х1, х2, х3
Таким образом, необходимо максимизировать показатель безопасности при ограничениях и найти значения х1, х2, х3:
67

2x1 x2 x3 25, |
|
||
x x x 14, |
|
||
1 |
2 |
3 |
|
|
4x2 |
2x3 19, |
|
0x1 |
|
||
|
0x2 |
x3 24, |
|
3x1 |
|
||
|
|
|
|
f (x) 6x1 5x2 5x3 |
max. |
||
Решение в СКМ «Маткад» представлено на рис. 3.16.
Рис. 3.16. Решение задачи обеспечения трёх параметров безопасности х1, х2, х3 в СКМ «Маткад»
Следовательно, максимум достигается при х1 = 5,5; х2 = 1;
х3 = 7,5.
И этот максимум есть 75,5:
6Р1 5Р2 5Р3 75.5.
68
Можно показать, что некоторые ресурсы остались (S1), т.е. можно считать, что «ценность» S1 меньше, чем других ресурсов
(рис. 3.17).
Вид |
Расход на единицу |
Запасы |
|
|
||
ресурса |
частного показателя |
ресурсов |
|
|
||
|
Т1 |
Т2 |
Т3 |
|
|
|
S1 |
2 |
1 |
1 |
25 |
5,5 |
? |
S2 |
1 |
1 |
1 |
14 |
0 |
? |
S3 |
0 |
4 |
2 |
19 |
0 |
? |
S4 |
3 |
0 |
1 |
24 |
0 |
? |
|
|
|
|
|
Остатки |
Теневая |
Системный эффект |
6 |
5 |
5 |
|
||
|
|
|
|
|
|
цена |
Оптимальный план |
5,5 |
1 |
7,5 |
|
|
|
Рис. 3.17. Остатки ресурсов при оптимальном решении
х1 = 5,5; х2 = 1; х3 = 7,5
А посему двойственная задача для задачи определения так называемой «теневой» цены ресурсов имеет вид (начинаем с нулевой переменной – в Маткаде с нуля идут):
|
|
2x1 x2 x3 25, |
|
|||
|
|
x x x 14, |
|
|||
|
|
|
1 |
2 |
3 |
|
|
|
|
|
4x2 |
2x3 19, |
|
|
|
0x1 |
|
|||
|
|
|
|
0x2 |
x3 24, |
|
|
|
3x1 |
|
|||
|
|
|
|
|
|
|
|
|
f (x) 6x1 5x2 5x3 max. |
||||
2x 1x 0x 3x 6, |
|
|||||
|
0 |
|
1 |
2 |
3 |
|
1x0 1x1 4x2 0x3 5, |
|
|||||
|
|
1x1 |
2x2 |
1x3 5, |
|
|
1x0 |
|
|||||
|
|
|
25x0 14x1 19x2 |
|
||
f (x) |
24x3 min. |
|||||
(3.6)
(3.7)
где (3.6) – исходная задача, т.е. (3.7) получается путем записи (3.6) по столбцам, ограничения берутся из целевой функции, причём если в исходной (прямой) задаче ищут максимум, то в двойственной – минимум.
69
Решаем (рис. 3.18).
Рис. 3.18. Решение двойственной задачи линейного программирования в СКМ «Маткад»
Такимобразом, получили«теневую» цену ресурсов(рис. 3.19).
Вид |
Расход на единицу |
Запасы |
|
|
||
ресурса |
частного показателя |
ресурсов |
|
|
||
|
Т1 |
Т2 |
Т3 |
|
|
|
S1 |
2 |
1 |
1 |
25 |
5,5 |
0 |
S2 |
1 |
1 |
1 |
14 |
0 |
3 |
S3 |
0 |
4 |
2 |
19 |
0 |
0,5 |
S4 |
3 |
0 |
1 |
24 |
0 |
1 |
Системный эффект |
6 |
5 |
5 |
|
Остатки |
Теневая |
|
|
|
|
|
|
цена |
Оптимальный план |
5,5 |
1 |
7,5 |
|
|
|
Рис. 3.19. Решение прямой и двойственной задач линейного программирования для примера (рис. 3.15)
70
