2629

Очевидно, что пустая цепочка является как левой, так и правой единицей в алгебраическом смысле: α = α = α.

Расширенные функции переходов и выходов [7]

Пусть A X , Y , Z, y0 , , ψ – конечный автомат. Расши-

ренными функциями переходов и выходов автомата называются функции, определённые не на входных символах, а на цепоч-

ках входных символов X * :

* :Y X * Y ,

* :Y X * Z* .

Определяются они так:

* ( y, ) y; * ( y,a ) * ( (y,a), );

* (y, ) y; * (y,a ) (y,a) * ( (y,a) ).

Достижимые и недостижимые состояния автомата [7]

Если в некоторые состояния автомата нет пути из начального состояния, то они называются недостижимыми, иначе – достижимыми. Недостижимые состояния для инициального автомата (у которого определено начальное состояние) можно удалить, они не влияют на поведение автомата.

Итак, некоторое состояние y автомата:

A X ,Y ,Z ,y0 , ,ψ

называют достижимым тогда и только тогда, когда существует цепочка α, приводящая к нему из начального состояния:

недостижимо_ y Неверно,что( α X * )[ * (y0 ,α) y] .

11

Иначе:

недостижимо_ y ( α X * )[ * (y0 ,α) y].

Эквивалентность автоматов [7]

Определение. Конечные автоматы А:

A X A ,YA ,ZA ,y0A , A , A

и В:

B X B ,YB ,ZB ,y0B , B , B

эквивалентны в случае:

1)если их входные алфавиты совпадают: X A X B X ;

2)реализуемые ими отображения совпадают:

( α X * )[ *A (y0A ,α) *Β (y0B ,α)].

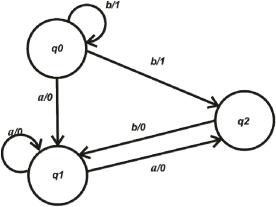
Пример [7]. Два конечных автомата А (рис. 1.2) и В (рис. 1.3) имеют разное число состояний и они по-разному называются.

Автомат А:

Рис. 1.2. Некоторый автомат А

12

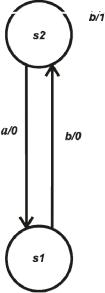
Автомат В:

Рис. 1.3. Некоторый автомат В

Но оказывается, их реакции на входную цепочку aabbabb одинаковы:

*A (y0A ,aabbabb) *B (y0B ,aabbabb) 0001001.

Однако перебрать все входные цепочки невозможно – их бесконечно много. Поэтому проблема эквивалентности автоматов нетривиальна.

Существует метод решения этой проблемы. Он основан на понятии прямого произведения автоматов.

Прямое произведение автоматов [7]

Определение. Прямым произведением автоматов

A X A ,YA ,ZA ,y0A , A , A ,

13

BX B ,YB ,ZB ,y0B , B , B

содинаковым входным алфавитом Х называется автомат А В:

A B X ,YA YB ,ZA ZB ,(y0A ,y0B ), A B ,ψA B ,

где

1)( yA YA )( yB YB )( x X )[ A B ((yA ,yB ), x)

=( A (yA , x), B (yB , x))];

2)( yA YA )( yB YB )( x X )[ A B ((yA ,yB ), )

=( A (yA , x), B (yB , x))].

Следовательно, в качестве состояний автомата А В получаем пары состояний(yA ,yB ) , начальное состояние – пара состоя-

ний (y0A ,y0B ) , выходной алфавит – множество пар выходных символов:

[( A (yA ,x), Β (yB ,x)].

Получаем параллельно работающие на одном входе автоматы (рис. 1.4):

Рис. 1.4. Прямое произведение автоматов А и В = А × В

14

Теорема Мура. Два конечных автомата:

A X A ,YA ,ZA ,y0A , , A ,

(yA ,yB ) в их прямом произведении А × В функции выходов одинаковы:

( x X )[ (yA ,x) (yB ,x)].

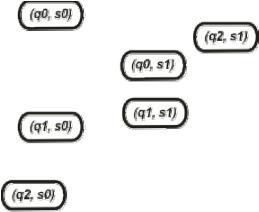
Умножим автомат А на автомат В. Получаем вначале вершины – их 6 (рис. 1.5).

Рис. 1.5. Получение вершин автомата А×В

Если есть петли в обеих вершинах, она остаётся и

ввершине графа произведения автоматов (b/1,1) – вверху,

вчислителе – входной символ, в знаменателе – выходные через запятую.

15

Дуги проводим так же (рис. 1.6).

Рис. 1.6. Начало получения дуг А × В

В результате получаем граф переходов А × В (рис. 1.7).

Рис. 1.7. Граф прямого произведения автоматов А и В – автомат А × В

16

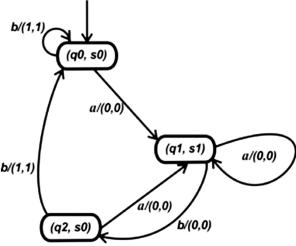
Удалим недостижимые состояния (рис. 1.8).

Рис. 1.8. Прямое произведение А × В с исключёнными недостижимыми состояниями

Видно, что для каждого состояния выполняется выдача пар одинаковых выходных сигналов. Следовательно, автоматы А и В эквивалентны.

Минимизация конечных автоматов

Итак, разные автоматы могут функционировать одинаково, даже если у них разное число состояний.

Важной задачей теории автоматов является нахождение минимального автомата, реализующего заданное автоматное отображение. В [8, 9] подробно рассмотрены вопросы минимизации логического преобразователя автомата, минимизация первичной таблица переходов. Детализируем вопрос минимизации числа состояний автомата.

Эквивалентные состояния [7]

Два состояния называются эквивалентными тогда и только тогда, когда их нельзя различить никакими входными последовательностями (экспериментами).

17

Двасостоянияp иq конечного автомата A X ,Y ,Z ,y0 , ,ψ называются эквивалентными (будем обозначать p q ) то-

гда и только тогда, когда

( X * )[ψ* (p,α) ψ* (q,α)].

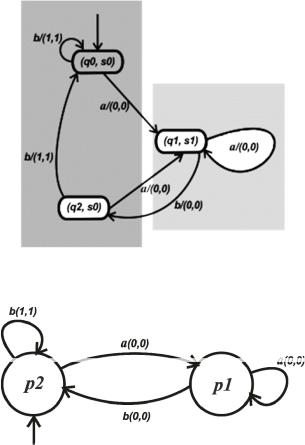
Пусть даны два автомата из предыдущей лекции – произведение А × В (рис. 1.9).

Рис. 1.9. Классы эквивалентности автомата А × В

Состояния q0 и q2 эквивалентны: любая входная цепочка, поданная на автомат, находящийся в состоянии q0, даст такую же реакцию и в случае, когда автомат находился вначале в состоянии q2.

Эти два состояния можно объединить в одно (рис. 1.10).

В результате получим автомат, имеющий два состояния

(рис. 1.11).

Эквивалентные состояния объединяются в классы, эти классы и являются состояниями нового автомата. Если определить на множестве состояний автомата минимально возможное

18

(меньше двух у автомата с памятью не бывает) разбиение, то и получим минимальный автомат, эквивалентный исходному.

Рис. 1.10. Объединение двух эквивалентных состояний в одно (получаем автомат с двумя состояниями)

Рис. 1.11. Автомат, эквивалентный автомату на рис. 1.9

Мы не сможем перебрать все возможные цепочки, как и в случае выяснения эквивалентности двух автоматов.

Но существует алгоритм последовательного разбиения состояний автомата на классы и определения максимального отношения эквивалентности.

19

Разбиениесостоянийавтоматанаклассыэквивалентности [7]

Алгоритм состоит в последовательном построении на множестве состояний автомата разбиений π0, π1,…, π∞, таких, что в один класс попадают k эквивалентные состояния, т.е. те, которые не различимы входными цепочками длиной k.

Такие состояния будем считать в отношении эквивалентности k .

В случае (p k q) , состояния p и q называются k-различи-

мыми.

Таким образом,

(p k q) ( X * , k)[ψ* (p,α) ψ* (q,α)].

Очевидно, что в любом автомате все состояния 0 эквивалентны, поскольку при подаче пустой цепочки на вход автомата (цепочки длиной 0) выходом является также пустая цепочка, независимо от того, в каком состоянии находится автомат.

Разбиения π0, содержащее один единственный блок и π1, в каждом блоке которого объединены состояния, не различимые входными сигналами, являются исходными при построении последовательности разбиений π0, π1,…, π∞.

Как же строить следующее разбиение, начиная с π1?

Теорема. Пусть p k q,k 1.

Для выполнения p k 1 q, необходимо и достаточно, чтобы

( x X )[ (p,x) k (q,x)].

Следовательно, k-эквивалентные состояния под воздействием входных сигналов переходили бы в состояния, также являющиеся k-эквивалентными.

Действительно, для того чтобы цепочка длиной k+1, например x0 , x1, x2 , ..., xk 1, не различала состояния p и q, нужно,

чтобы из этих состояний под воздействием сигнала x0 перешла в такие состояния, которые не различимы цепочкойx1 , x2 ,...., xk , т.е. чтобы (p,x) и (q,x) были k-неразличимы (рис. 1.12).

20