
2629
.pdf
|
|
|
|
Таблица 1 . 1 0 |
|
Карта Карно минимизации функции у1(t + 1) |
|||||
|
ab |
|
|
|
|
у2у1(t) |
|
11 |
|
|
|
|
00 |
01 |
|
10 |
|
00 |
0 |
0 |
~ |
|
1 |
01 |
1 |
~ |
1 |
|
1 |
11 |
~ |
1 |
1 |
|
1 |
10 |
~ |
~ |
~ |
|
~ |
|
|
|
|
Таблица 1 . 1 1 |
|
|
Карта Карно минимизации функции z1 |
||||
|
ab |
|
|
|
|
у2у1(t) |
|
11 |
|
|
|
|
00 |
01 |
|
10 |
|
00 |
0 |
0 |
~ |
|
0 |
01 |
0 |
~ |
0 |
|
0 |
11 |
~ |
0 |
0 |
|
1 |
10 |
~ |
~ |
~ |
|
~ |
На основании данной таблицы функция для z1 будет выглядеть следующим образом:
|
|
z1 y2 (t) |
|
. |
|
|
|
|
|
b |
|
|
|
||
|
|
|
|
|
|
Таблица 1 . 1 2 |
|
|
Карта Карно минимизации функции z2 |
||||||
|
ab |
|
|
|
|
|
|
у2у1(t) |
|
|
|
11 |
|
|
|
|
00 |
01 |
|
|
|
10 |
|
00 |
0 |
1 |
|
|
~ |
|
0 |
01 |
1 |
~ |
|
|
0 |
|
0 |
11 |
~ |
1 |
|
|
0 |
|
0 |
10 |
~ |
~ |
|
|
~ |
|
~ |
На основании данной таблицы функция для z1 будет выглядеть следующим образом:
31
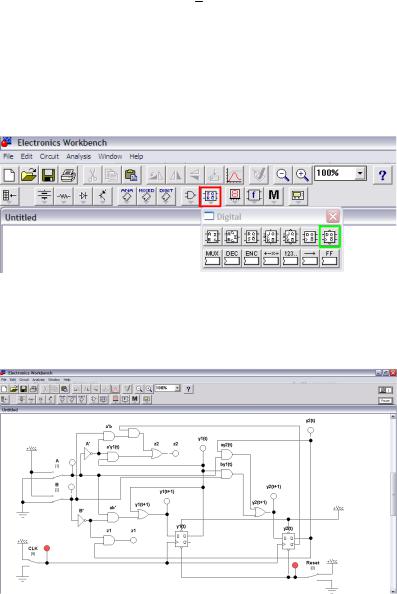
z2 y1 t aVaby2 t .
На основании полученных функций моделируем автомат на жесткой логике, используя приложение Electronics Workbench. Для реализации данного автомата-распознавателя будем использовать как элемент памяти D-триггер и элементы «жесткой» логики. Расположение элемента памяти приведено на рис. 1.17.
Рис. 1.17. Расположение D-триггера
На рис. 1.18–1.26 представлен автомат-распознаватель последовательности 0232 и разные его состояния.
Рис. 1.18. Автомат – распознаватель последовательности 0232
32
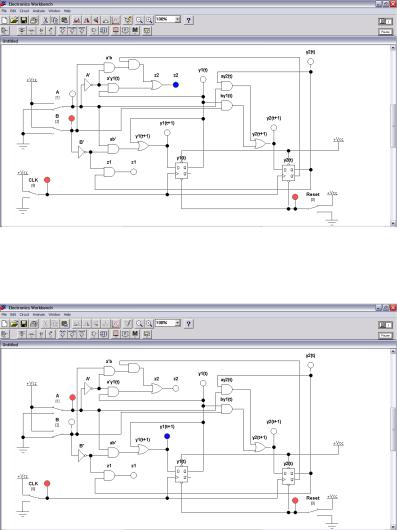
Рис. 1.19. Состояние автомата-распознавателя последовательности 0232
(соответствует клетке 1 таблицы переходов-выходов)
Рис. 1.20. Состояние автомата-распознавателя последовательности 0232
(соответствует клетке 2 таблицы переходов-выходов)
33
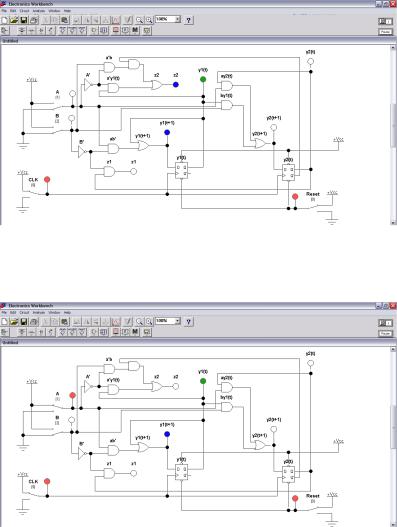
Рис. 1.21. Состояние автомата-распознавателя последовательности 0232
(соответствует клетке 4 таблицы переходов-выходов)
Рис. 1.22. Состояние автомата-распознавателя последовательности 0232
(соответствует клетке 6 таблицы переходов-выходов)
34

Рис. 1.23. Состояние автомата-распознавателя последовательности 0232
(соответствует клетке 7 таблицы переходов-выходов)
Рис. 1.24. Состояние автомата-распознавателя последовательности 0232
(соответствует клетке 13 таблицы переходов-выходов)
35
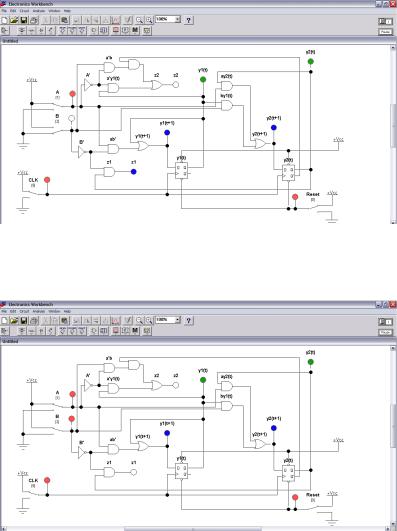
Рис. 1.25. Состояние автомата-распознавателя последовательности 0232
(соответствует клетке 14 таблицы переходов-выходов)
Рис. 1.26. Состояние автомата-распознавателя последовательности 0232
(соответствует клетке 15 таблицы переходов-выходов)
Как видно из рисунков, модель автомата-распознавателя последовательности0232 соответствуеттаблицепереходов–выходов.
36
2. КОМБИНАТОРНЫЕ МОДЕЛИ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ
2.1. Комбинаторные вычисления. «Проклятие» размерности
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 г. опубликовал свой труд «Рассуждения о комбинаторном искусстве» [11].
Основная задача комбинаторики, как раздела дискретной математики, – пересчет и перечисление элементов в конечных множествах.
Если требуется определить, сколько элементов, принадлежащих заданному конечному множеству, обладает некоторым свойством или заданным набором свойств, то это задача пересчета. Если необходимо выделить все элементы множества, удовлетворяющие заданным свойствам, то это задача перечисления.
В некоторых задачах на исходном конечном множестве элементов определена целевая функция, причем нас интересуют элементы множества, соответствующие минимальному или максимальному значению этой функции. В этом случае решается задача оптимизации.
При этом под решением задачи оптимизации «в сильном смысле» понимается нахождение всех элементов, минимизирующих (максимизирующих) целевую функцию, а под решением задачи оптимизации «в слабом смысле» – нахождение единственного произвольного элемента.
Вычисления на конечных математических структурах часто называют комбинаторными вычислениями, и они требуют комбинаторного анализа для установления свойств и оценки применимости используемых алгоритмов.
Комбинаторные задачи могут быть решены, например, системой компьютерной математики Matematica фирмы Wolfram Research,Inc. – пакет расширения «Дискретная математика»
(DiscreteMath) – комбинаторика и ее функции (Combinatorica, CombinatorialFunctions): функции перестановок и сочетаний и др.
37
Если при малой размерности переборные, комбинаторные оптимизационные задачи решаются довольно легко, то при большой размерности задачи полный перебор вариантов становится нереализуемым, поэтому математики используют выражение «проклятие размерности».
Комбинаторная оптимизация – область теории оптимизации в прикладной математике, связанная с исследованием операций, теорией алгоритмов и теорией вычислительной сложности.
Вкомбинаторной оптимизации используются как математические подходы, так и методы искусственного интеллекта.
Алгоритмы комбинаторной оптимизации, одним из наиболее популярных среди них является метод ветвей и границ, позволяют уменьшать пространство допустимых решений с помощью эффективной процедуры поиска.
Полный перебор (или метод «грубой силы» от англ. brute force) – метод решения задачи путем перебора всех возможных вариантов. Сложность полного перебора зависит от размерности пространства всех возможных решений задачи.
Вкриптографии на сложности полного перебора основывается оценка криптостойкости шифров. В частности, шифр считается криптостойким, если не существует метода «взлома», существенно более быстрого, чем полный перебор всех ключей.
«Жадный» алгоритм – алгоритм, заключающийся в принятии локально оптимальных решений на каждом этапе, допуская, что конечное решение также окажется оптимальным.
2.2. Задача SAT, P и NP,
NP – полные алгоритмы [12, 13]
При построении функции сложности исходят из наибо-
лее худшего случая – Worst-case analysis.
Сложностью задачи называется сложность наилучшего алгоритма.
Полиномиальным алгоритмом (или алгоритмом полиномиальной временной сложности) называется алгоритм, у которого
38
временная сложность равна О(Р(n)), где Р(n) – некоторая полиномиальная функция от входной длины n.
Алгоритмы, для временной сложности которых не существует такой оценки, называются экспоненциальными – класс Е.
Полиномиальные алгоритмы – «хорошие». Экспоненциальные – «плохие»
Это разделение условно, так как при большой степени (>4) полиномиальный алгоритм становится «плохим».
Задача считается труднорешаемой, если для нее не существует разрешающего полиномиального алгоритма.
NP-сложные задачи
В так называемом недетерминированном алгоритме (существует и недетерминированная машина Тьюринга – НДМТ) варианты «угадываются» случайным образом, тогда, если повезет, можно относительно быстро найти вариант, удовлетворяющий заданным ограничениям. Иногда представляют НДМТ проверяющей все альтернативы одновременно.
Такие задачи, имеющие недетерминированное решение, которое иногда удается найти за полиномиальное время, называются недетерминировано полиномиальными NP (Nondeterministic Polynomial).
Преобладает мнение, что детерминированных алгоритмов решения таких задач не существует.
Для сокращения перебора вариантов при решении таких комбинаторных задач (задач комбинаторной сложности) предлагаются различные способы «борьбы с перебором, борьбы с проклятием размерности».
Например, при решении задачи коммивояжёра решение задачи – совокупность рёбер. За полиномиальное время можно убедиться, что найденный цикл – гамильтонов. Но лучшей ли это вариант? Вопрос открытый…
Большинство практически важных задач относится к классу NP.
39
Поиск «хороших» алгоритмов – благородная задача, но для многих задач их найти не удаётся. Вопрос Р NP? Р=NP? Более тридцати лет ждёт своего решения.
Математический институт Clay Mathematics Institute USA
предлагает приз 1.000.000 $ за решение этой проблемы.
NP-полные задачи
Для некоторых NP-задач было обнаружено удивительное свойство. Оказалось, что они универсальны в том смысле, что построение полиномиального алгоритма для них влечёт автоматически возможность построения такого же алгоритма для всех задач NP. Такие задачи называют NP-полные.
Всякий алгоритм обладает свойством массовости – он решает не одну задачу, а некоторый класс задач. Множество конкретных или индивидуальных задач (instances) называют массовой задачей (decision problem). Пусть имеются две массовые задачи Z1, Z2 из NP,
Z1 полиномиально сводится к Z2, если:
1.Для любой индивидуальной задачи из Z1 можно за полиномиальное время построить соответствующую индивидуальную задачу Z2.
2.Решение построенной индивидуальной задачи из Z2 за полиномиальное время может быть преобразовано в решение Z1.
Массовую задачу Z называют NP полной, если любая задача из класса NP полиномиально сводится к задаче Z.
Исторически первой NP-полной задачей является задача выполнимости КНФ – SAT (Satisfiability). В настоящее время найдены сотни таких задач.
Задача выполнимости булевых формул (SAT или ВЫП) –
задача распознавания, важная для теории вычислительной сложности.
Экземпляром задачи SAT является булева формула, состоящая только из имен переменных, скобок и операций 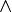 (И),
(И),
40
