Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

387

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

3.83 Mб

Скачать

☆

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 2425 / 2925 26 27 28 29 > Следующая >>>

УДК 621.396

И.Н. Липатов, В.Н. Лясин, Г.И. Рустамханова

Пермский государственный технический университет

ЦИФРОВОЕ МОДЕЛИРОВАНИЕ ДИФФЕРЕНЦИРУЕМОГО СЛУЧАЙНОГО ПРОЦЕССА С ИСПОЛЬЗОВАНИЕМ ФОРМИРУЮЩЕГО ФИЛЬТРА

Рассматривается задача построения формирующего фильтра, предназначенного для цифрового моделирования дифференцируемого случайного процесса. Формирующий фильтр реализован на ЦВМ. Приводятсярезультатымоделированияслучайногопроцесса.

Решается задача цифрового моделирования дифференцируемого случайного процесса m(t) с использованием формирующего фильтра (ФФ). Корреляционная функция процесса m(t) определяется соотношением [1].

Km (τ) = σm2 e−µ	τ	(cosλτ +	µsin λ	τ	) ,	(1)


			λ

где σ2m ,µ,λ – дисперсия, коэффициент нерегулярности и преобладающая частота в спектре процесса m(t) .

Двухсторонняя спектральная плотность Sm* (ω) процесса m(t) определяется формулой [2]

		∞
Sm* (ω) = ∫Km (τ)e− jωτdτ,						(2)
		−∞
где ω – круговая частота, рад/с.
Подставим (1) в (2). Имеем [1]
Sm* (ω) =			Fb2		,	(3)
Sm* (ω) =		ω4 + 2aω2 + b4			,	(3)
где		ω4 + 2aω2 + b4
где
a = µ2 − λ2 ;			b2 = µ2	+ λ2 ;		(4)
	F = 4σm2 µ.					(5)
						241

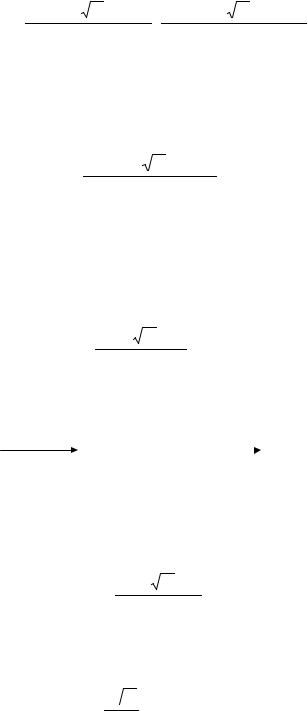
Представим формулу (3) в виде [1]

S* (ω) =

b F

(− jω)2

b F

( jω)2 + 2µ( jω) +b2

+ 2µ(− jω) +b2

Запишем формулу (6) в виде

где

Sm* (ω) =

H ( jω)

2 Sv* (ω),

H ( jω)

2 = H ( jω) H (− jω);

H ( jω) = ( jω)2 + 2µ( jω) +b2

;

(6)

(7)

(8)

(9)

S*(ω) =C =1.		(10)
v	0

Здесь H ( jω) – передаточная функция ФФ; Sv* (ω) – двухсторонняя спектральная плотность случайного процесса v(t) типа белого шума; C0 – интенсивность белого шума.

Из (9) имеем
b F
H (s) = s2 + 2µs + b2 .	(11)

На рис. 1 показана схема ФФ. Здесь h(t) – весовая функция ФФ.

v(t)	ФФ,	m(t)
	H(s), h(t)

Sv* (ω) = C0

Рис. 1. Схема ФФ

Определим весовую функцию h(t) ФФ. представим в виде

H (s) =	b	F	2 .
	(s + µ)	2
			+ λ

Из (12) имеем

h(t) = L−1{H (s)}

или [3]

h(t) = bλF e−µt sin λt .

Соотношение (11)

(12)

(13)

(14)

242

Здесь

L−1 { } – обратное

преобразование Лапласа от

выражения

в скобках.

Случайные процессы m(t) и v(t)

связаны соотношением [4]

∞

m(t) = ∫h(τ)v(t − τ)dτ.

(15)

Случайная последовательность v[i] = v(ti ), ti = i∆t; i =

есть

0, n2

дискретный белый шум с

нулевым

математическим

ожиданием

и дисперсией σv2 вида [5,6]

σ2

(16)

∆t

где ∆t

– интервал дискретности измерений.

Из соотношения (14) имеем

h[i] = k*e

−µ*i

sin λ*i, i = 0, N ;

(17)

(18)

где

h1[N] ≤ 0,01,

e−µ*i ;

h [i] = k

(19)

k* = b F

;

µ*

=µ∆t; λ* = λ∆t.

(20)

Здесь h[i] = h(ti ), ti	=i∆t.
При реализации на ЦВМ формулы (15) выполним численное
интегрирование по методу трапеций			ˆ
N −1h[l] v[i −l] + h[l +1] v[i −l −1]
ˆ
m[i] = ∑		∆t, i = N, n3		(21)
	2
l =0
где v[i −l] = v(ti−l ); ti−l = (i −l)∆t. Запишем соотношение
	ˆ			(22)

	m[i] = m[i + N], i = 0, n2 .
Таким образом, ФФ определяется соотношениями (17)–(22), (16).
Рассмотрим реализацию m(t) длиной Tr . Разобьем ее, как пока-
зано на рис. 2, на nd	смежных отрезков длиной Т каждый и обозначим

эти отрезки через mi (t), (i −1)T ≤ t ≤ iT , где i =1, nd . Из рис. 2 следует, что длина реализации случайного процесса m(t) определяется соотношением

Tr = ndT .

243

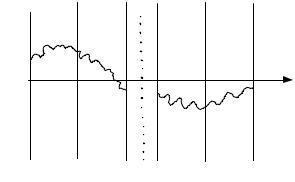
m(t)

0 T 2T (nd − 2)T (nd −1)T ndT

Рис. 2. Реализация m(t), разбитая на nd смежных отрезков длиной Т каждый

Будем считать, что T = N∆t . При дискретном временном параметре каждая реализация mi (t) представлена n 6* = N +1 значениями временного ряда

m [i, n* ] = m[N(i −1) + n* ]; i =

1, n

; n* =

0, N,

(23)

где

m[N(i −1) + n* ] = m(N(i −1)∆t + n*∆t) .

Для получения оценок σˆ m ,µˆ

, λ параметров σm ,µ, λ будем ис-

пользовать оценку

Sm ( fk ), k = 0, n5 ;

n5 =

односторонней

спек-

тральной плотности

Sm ( fk ) = 2Sm* ( fk )

случайной последовательно-

сти m[i], i =

на дискретных частотах. Здесь

0, n2

= k∆f ; ∆f =

; k =

0, n5

определяется соотношением [7]

Оценка Sm ( fk )

Sm ( fk ) =

∑

X i ( fk )

, k = 0, n5

nd N∆t i=1

(24)

(25)

где
		N −1	−	π	*	(26)
Xi ( fk ) = ∆t ∑m[i,n ] exp				j2 kn	.	(26)
		n* =0		N
Здесь Xi ( fk ), i =		– коэффициенты		Фурье для i-й последова-
Здесь Xi ( fk ), i =	1,nd	– коэффициенты		Фурье для i-й последова-
тельности m [i, n* ].
*

244

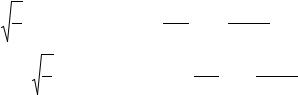
Представим Xi ( fk )

в виде

X i ( fk ) =Pi ( fk ) + jQi ( fk ), i =

; k =

(27)

1, nd

0, n5

где [7]

P( f

) = ∆t

N −1

]

− cos

2 πn*

2πkn*

∑

[i,n

cos

3 n* =0

8 N −1

2 πn*

(28)

( f

) = (−1)∆t

]

− cos

2πkn*

∑

[i,n

sin

3 n* =0

Из (27) имеем

( f

)

= P2

( f

) + Q2

( f

(29)

определяется с использованием

Таким образом, оценка Sm ( fk )

соотношений (25), (29), (28).

Рассмотрим последовательность действий, которые были вы-

полнены для получения оценок σˆ m ,µˆ , λ. Случайная последователь-

ность

m[i],

i =

реализована с применением ФФ.

По формулам

0, n2

(25),

(29),

(28) определялась оценка Sm ( fk ) односторонней спек-

тральной плотности последовательности m[i],

i =

0, n2

Введем обозначение

(30)

r1[k] = Sm ( fk ); k = 0, n5 ,

где r1[k] – одномерный массив чисел с индексом k.

Первоначально определим оценку λ параметра λ. Найдем мак-

симальный элемент в массиве r [k],

k =

и индекс k = k * для это-

0, n

го элемента. Тогда λ определяется в виде

(31)

λ = 2πk2 ∆f .

Определим оценку σˆ m2 дисперсии σm2 , используя численное ин-

тегрирование по методу трапеций

] + r1[k +1].

(32)

σˆ m2 = ∆f ∑ r1[k

n5 −1

k =0

Найдем оценку ˆ параметра µ. Будем аппроксимировать r1[k]

при k =

выражением

0, n5

245

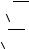
S m0 [ fk ] =

где

aˆ

Введем обозначение

					2	ˆ2
				8σˆ mµˆb						,
(2πfk )			4	+ 2aˆ(2πfk )				2	ˆ4	,
(2πfk )				+ 2aˆ(2πfk )					+ b
=µˆ	2			ˆ2	ˆ2	= µˆ	2		ˆ2
=µˆ		− λ			; b	= µˆ			+ λ .

x1[k1 ] = µˆ, k1 =1,2,...

Соотношение (33) с учетом (35) примет вид

						2	ˆ2	x1[k1 ]
S 0	[ f	k	] =		8σˆ mb1						,
					4				2
m				(2πfk )		+ 2aˆ1		(2πfk )		ˆ4
										+ b1
где				ˆ2			ˆ2			ˆ2
			2			;		2
	aˆ1 = x1			[k1 ] − λ			b1	= x1 [k1		] + λ .

Отобразим массив ε2 [k] , определяемый по формуле

[k] = S

[k] − r [k], k =

0, n

Определим величину d1 вида

1 ∑5

ε2

[k].

+1 k =0

(33)

(34)

(35)

(36)

(37)

(38)

(39)

Будем подбирать такое значение ˆ , при котором d1 принимает минимальное значение. Введем массив S1[k1 ] = d1 , k1 =1,2,...

Следовательно, задача сводится к поиску минимального элемента в

массиве	S1[k1 ], k1 =1,2,... и индекса k1 = k1* этого элемента. Предпо-
лагалось,	что при		k1 =1, µˆ = 0 . Осуществлялось синхронное измене-
ние k1 , µˆ	и x1[k1 ]		по формулам
		k1 = k1 +1; µˆ = µˆ + 0,01; x1[k1 ] =µˆ,						(40)
т.е. k1, µˆ	и x1[k1 ]	принимали значения
k1 = 2; µˆ = 0,01; x1[2] = 0,01;						k1 = 3; µˆ = 0,02; x1[3] = 0,02;
			k1 = 4; µˆ = 0,03;				x1[4] = 0,03
и так далее. Изменение µˆ					осуществлять в диапазоне 0 ≤ µˆ ≤ P1 . При
расчетах	принималось P1				= 2µ.	В	результате получены	массивы
x1[k1] , S1[k1] , k1 =				, где
x1[k1] , S1[k1] , k1 =			1,k6	, где
						P
					k6 =	1	+1.	(41)
					k6 =		+1.	(41)
					0,01
246

При P1 =1 k1 =101.

Определение

минимального

элемента

в массиве

S1[k1 ] ,

индекса

этого элемента

k1 = k1*

позволяет из

массива

1, k6

x [k

] при k

= k *

извлечь то значение ˆ , при котором обеспечивает-

ся наилучшая аппроксимация r1[k] , k = 0, n5 выражением (36). Таким способом получена оценка ˆ параметра .

ФФ был реализован на ЦВМ.			Предполагалось,		что ∆t = 0,1c;
σm = 20;	µ = 0,4c−1 ;	λ = 2c−1 ; C0	=1;	N = 200; n5	=100; nd = 4;
n2 = 900;	n3 =1300;	T = N∆t = 20c;	n4	= nd N = 800 . Получены сле-

дующие значения оценок σˆ m ,µˆ ,λˆ :

σˆ m =17,7; µˆ = 0,44c−1 ; λˆ =1,885c−1 .

Таким образом, ФФ с достаточной точностью моделирует дифференцируемый случайный процесс m(t) , описываемый корреляционной функцией вида (1).

Библиографический список

1.Ривкин С.С. Статистический синтез гироскопических устройств / С.С. Ривкин. – Л.: Судостроение, 1970.

2.Солодовников В.В. Статистическая динамика систем автоматического управления / В.В. Солодовников. – М.: Физматгиз, 1960.

3.Задачник по теории автоматического управления / под общей ред. А.С. Шаталова. – М.: Энергия, 1971.

4.Бессонов А.А. Методы и средства идентификации динамических объектов / А.А. Бессонов, Ю.В. Загашвили, А.С. Маркелов. – Л.: Энергоатомиздат, 1989.

5.Быков В.В. Цифровое моделирование в статистической радиотехнике / В.В. Быков. – М.: Сов. радио, 1971.

6.Тихонов В.И. Статистический анализ и синтез радиотехнических устройствисистем / В.И. Тихонов, В.Н. Харисов. – М.: Наука, 1991.

7.Бендат Дж. Прикладной анализ случайных данных / Дж. Бендат, А. Пирсол. – М.: Мир, 1989.

Получено 25.01.2007

247

УДК 621.37

Г.И. Пахомов, Ю.Г. Пахомов

Пермский государственный технический университет

ПРИМЕНЕНИЕ ВЕЙВЛЕТОВ ДЛЯ ОБРАБОТКИ СИГНАЛОВ

Рассмотрено применение вейвлетов (wavelets) для построения спектрограмм реальных звуковых сигналов с целью идентификации их тонких локальных особенностей. Вейвлетанализ осуществляется на базе пакета расширения системы

MATLAB 7.0 Wavelet Toolbox.

Для частотно-временного анализа непериодических сигналов в настоящее время используется вейвлетное преобразование (wavelet transform) [1]. Вейвлетное преобразование применяется также для фильтрации сигналов, устранения шумов, определения местонахождения сингулярностей и их распределения.

Физический принцип неопределенности, перенесенный в область обработки сигналов, говорит о том, что нельзя одновременно

слюбой точностью определить время и частоту. Если разрешение по времени высокое, то частота будет определяться менее точно, и наоборот. Может оказаться достаточно сложно одновременно измерить

снеобходимой степенью точности частоту компоненты сигнала и время ее появления или разделить во времени различные частотные компоненты. Для решения этой общей проблемы частотно-временного анализа и используется вейвлет-преобразование.

Набор вейвлетов, в их временном или частотном представлении, может приближать сложный сигнал или изображение, причем идеально точно или с некоторой погрешностью. Вейвлеты имеют явные преимущества в представлении локальных особенностей функций по сравнению с рядами Фурье. Благодаря этому вейвлеты нашли практическое применение для анализа тонких особенностей сложных сигналов и изображений, для их сжатия и очистки от шума.

248

Общепринятым подходом к анализу широкополосных импульсных и цифровых сигналов s(t) является их представление в виде взвешенной суммы простых составляющих – базисных функций ψk (t) , помноженных на коэффициенты Ck:

s(t) = ∑Ck ψk (t) .	(1)
k
Так как базисные функции ψk (t) зафиксированы как функции оп-
ределенного типа, только коэффициенты Ck содержат	информацию

о конкретном сигнале. Таким образом, можно говорить о возможности представления произвольных сигналов на основе рядов с различными базисными функциями. Ряд Фурье использует в качестве базисных функций синусоиды. Они предельно локализованы в частотной области (вырождаясь на спектрограмме в вертикальную линию), но вообще не локализованы во временной области. Противоположный пример – импульсная базисная функция

1,k = t, ψk (t) = δk (t) = 0,k ≠ t.

Она четко локализована во временной области, и потому идеально подходит для представления разрывов сигнала. Но эта базисная функция не несет информации о частоте сигнала и потому плохо приспособлена для представления сигналов на заданном отрезке времени и тем более периодических сигналов. Вейвлеты занимают промежуточное положение между рассмотренными крайними случаями и образуют некоторый набор функций, удовлетворяющих ряду условий и основанных на использовании представления сигнала в виде (1).

Как известно, в вейвлетном преобразовании в качестве весовых коэффициентов значений сигнала выступают вейвлетные функции. Из ряда основных (базовых) вейвлетных функций, из которых получаются все остальные (дочерние) вейвлет-функции, может быть выбрана функция, обеспечивающая получение определенных свойств сигнала. То есть, конкретный выбор того или иного вейвлета целиком зависит от характера поставленной задачи и от вида анализируемого сигнала.

К базовой вейвлет-функции предъявляется ряд требований:

− она должна осциллировать вокруг нуля в окрестности неко-

∞

торой точки на оси t, причем ∫ Ψ(t)dt = 0 ;

−∞

249

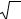
− нормафункцийдолжнабытьконечной,	ψ	∞	ψ	2	1/ 2
		∞		2	1/ 2
		= ∫			(t)dt	< +∞;
		−∞

−функция не должна содержать компонентов постоянного тока;

−должна быстро спадать во времени до нуля;

−должна быть обратимой.

Последнее свойство гарантирует, что вейвлетное преобразование сигнала будет однозначным.

Примером базовой вейвлет-функции может служить хорошо изученный вейвлет

ψ(t) = (t2 −1)exp(−t2 / 2),

являющийся второй производной гауссова импульса exp(–t2/2). Вейвлетная функция ψ(t) удовлетворяет вышеизложенным требованиям, т.е. осциллирует и спадает до нуля.

Дочерние вейвлет-функции получают путем такого изменения масштаба базовой, чтобы образовалось семейство функций. Каждую дочернюю функцию можно записать как

1	ψ{(t − τ)/ a},	(2)
a

где а – переменный коэффициент масштабирования, а τ – константа переноса. Если масштаб а увеличивается, то амплитуда и аргумент функции уменьшаются. Уменьшение аргумента при заданной амплитуде означает, что уменьшается частота. Следовательно, увеличение масштаба а соответствует уменьшению частоты, и поэтому функция расширяется во временной области по горизонтали. Положительные значения константы переноса приводят к переносу функции вдоль положительной временной оси. Итак, с помощью коэффициента масштабирования а и константы переноса τ можно создавать функции с большими или меньшими амплитудами, с высшими или низшими частотами и размещать их в различные моменты времени. Таким образом, нестационарные сигналы с различными частотными компонентами, расположенными в различных промежутках времени, можно описывать как сумму различных вейвлетных функций. Число используемых при разложении сигнала вейвлетов задает уровень декомпозиции сигнала.

250

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 2425 / 2925 26 27 28 29 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20221.38 Mб3371.pdf
#
15.11.20221.4 Mб2374.pdf
#
15.11.20221.4 Mб3377.pdf
#
15.11.20221.4 Mб3378.pdf
#
15.11.20221.45 Mб1384.pdf
#
15.11.20223.83 Mб5387.pdf
#
15.11.20221.46 Mб2388.pdf
#
15.11.2022274.76 Кб039.pdf
#
15.11.20224.07 Mб63G Evolution. HSPA and LTE for Mobile Broadband.pdf
#
15.11.202295.04 Кб04.pdf
#
15.11.2022274.86 Кб040.pdf