284

Окончание итерационного процесса для метода простой итерации будет заключаться в выполнении одного из следующих условий:

условия близости значений корня для двух последовательных приближений: xk xk 1 ;

условия близости значения функции в точке xk к нулю:

F xk .

Графически метод простой итерации для отыскания решения уравнения (3.1) на отрезке a;b представляет собой опре-

деление точки пересечения графиков двух линий y f x

иy x (рис. 3.2). При этом предполагается наличие некоторого начального приближения x0 , расположенного на отрезке a;b ,

исамо искомое решение вместе со всеми итерациями не выходит за пределы этого отрезка.

Рис. 3.2. Иллюстрация метода простой итерации

161

elib.pstu.ru

На рис. 3.2 итерационный процесс метода представлен в виде стрелочек, указывающих направление движения процесса. В данном случае процесс сходится, так как при неограниченном числе итераций можно сколь угодно близко получить решение уравнения (3.2).

Рассмотрим сходимость метода простой итерации. Достаточным условием сходимости является непрерывность и огра-

Если f x 1, то итерационный процесс может не сходиться. При выполнении условия f x 1 лишь вблизи решения, а не на всем отрезке a;b итерационный процесс может сойтись при

выборе начального приближения достаточно близко к искомому решению. Таким образом, в методе простой итерации важен выбор начального приближения.

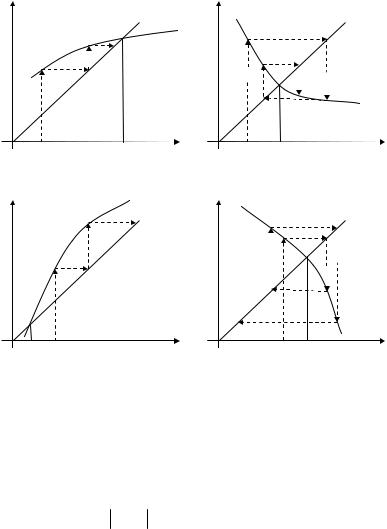
На рис. 3.3 представлены четыре случая взаимного распо-

Рис. 3.3, а и рис. 3.3, б соответствуют случаю сходимости ите-

и рис. 3.3, г соответствуют случаю расходимости процесса f x 1. При этом также имеет место односторонняя и двусторонняя расходимость.

Отметим то, что условие f x 1 сходимости метода ите-

раций является достаточным, т.е. выполнение этого условия гарантирует сходимость итерационного процесса, но невыполнение условия не означает, что процесс окажется расходящимся. При этом все приближения должны попадать в отрезок отделе-

162

elib.pstu.ru

ния корня a;b . Например, для случая, представленного на

y f x

Скорость сходимости метода зависит от параметра q , входящего в условие f x q 1. Чем меньше этот параметр, тем

163

elib.pstu.ru

быстрее по методу итераций можно определить корень уравнения (3.2). Исходное уравнение (3.1) может быть преобразовано к виду (3.2) многими способами, и, очевидно, для метода итера-

ции целесообразно выбирать такой вид функции f x , для которой параметр q имеет наименьшее значение.

y f x

Рис. 3.4. Иллюстрация сходимости метода простой итерации при невыполнении условия f x 1

Рассмотрим один из вариантов перехода от уравнения (3.1) к уравнению (3.2):

F x 0 , F x 0 , x x F x .

Здесь 0 – некоторое число. Таким образом, мы получили уравнение (3.2) с правой частью в виде функции f x x F x . За счет выбора значения параметра можно

добиваться сходимости метода простой итерации и повышения скорости сходимости. Например, если на некотором отрезке

164

elib.pstu.ru

a;b , содержащем корень уравнения, производная F x огра-

ничена константами m и М:

0 m F x M ,

f x 1, то есть сходимость метода простой итерации. Параметр можно выбирать в зависимости от номера ите-

рации k. Так, если положить k 1 , то итерационный

F xk

процесс метода простой итерации примет вид

xk f xk 1 , xk xk 1 k 1F xk 1 ,

xk xk 1 F xk 1 . F xk 1

Полученное соотношение совпадает с формулой итерационного процесса метода Ньютона. Следовательно, метод Ньютона можно трактовать как частный случай метода простой итерации.

При реализации метода простой итерации следует помнить о его возможном расхождении. Поэтому в условие завершения итерационного процесса включают условие ограничения числа итераций, то есть при совершении методом большого числа итераций производится остановка процесса, уточнение параметров метода и новый запуск.

Метод простой итерации обобщается на случай решения систем нелинейных уравнений.

165

elib.pstu.ru

3.3. Метод Ньютона

Пусть задана функция F x непрерывная и дважды дифференцируемая на отрезке a;b . Необходимо отыскать решение уравнения (3.1). При этом подразумевается, что на отрезке a;b

решение существует и единственно.

Построение итерационного процесса отыскания решения уравнения (3.1) по методу Ньютона сводится к построению на

и отысканию точки пересечения этой касательной с осью абсцисс. Метод Ньютона, или, как его называют по-другому, метод касательных, так же как и метод простой итерации, требует наличия начального приближения, т.е. точки, для которой строится первая касательная. При этом необходимо, чтобы все при-

ближения располагались внутри отрезка a;b .

Уравнение касательной к линии y F x в точке

xk ; F x0 имеет вид

y F x0 F x0 x x0 .

Следующее приближение находим как точку пересечения касательной с осью x:

x1 x0 F x0 .

F x0

Аналогичным образом определяются последующие точки приближения. В общем виде итерационный процесс метода Ньютона выглядит так:

xk xk 1 F xk 1 . F xk 1

При этом необходимо выполнение условия F xk 1 0 . Окончание итерационного процесса для метода простой итера-

166

elib.pstu.ru

ции будет заключаться в выполнении одного из следующих условий:

условия близости значений корня для двух последовательных приближений: xk xk 1 ;

условия близости значения функции в точке xk к нулю:

F xk .

Графическое представление метод Ньютона изображено на рис. 3.5.

y

0

F x1

F a

Рис. 3.5. Иллюстрация метода Ньютона

Нужно отметить, что на каждой итерации объем вычислений в методе Ньютона больше, чем в методе деления пополам, поскольку приходится находить значение не только функции

F x , но и значение ее производной. Однако скорость сходимо-

сти этого метода значительно выше.

Достаточное условие сходимости метода Ньютона получим из соответствующего условия для метода простой итерации, так как выше было показано, что метод Ньютона представляет со-

167

elib.pstu.ru

бой частный случай метода простой итерации, в котором

f x x F x .

F x

Используя условие сходимости метода простой итерации f x 1, нетрудно получить достаточное условие сходимости

метода Ньютона:

F x F x F x 2 .

Поскольку F x 0 и F x 0 , то итерационный процесс метода Ньютона сходится к точному значению корня на отрезкеa;b при произвольном начальном приближении.

Достоинства метода Ньютона состоят в его высокой сходимости, возможности обобщения на случай систем уравнений, а также в том, что он является одношаговым. Однако метод

Ньютона расходится в тех областях, где F x 0 . Кроме того, если функция F x задана таблично, то вычисление F x затруднено.

168

elib.pstu.ru

4. РАБОЧЕЕ ЗАДАНИЕ «ПЛАНИРОВАНИЕ ИНВЕСТИЦИЙ КАПИТАЛА ДЛЯ ПОЛУЧЕНИЯ ЗАДАННЫХ ПРИБЫЛЕЙ»

4.1. Постановка задачи

Прибыль z некоторого предприятия является функцией от начального капиталовложения x. Известно, что при капиталовложении x0 прибыль составляет z0 . Определить необходимые

капиталовложения xk на каждый сезон работы, позволяющие

получить предприятию заданные прибыли zk , где индекс k ука-

зывает номер рассматриваемого сезона и меняется в пределах от 1 до n, n – общее число сезонов работы предприятия. Вид функ-

циональной зависимости z f x и число n выбираются по но-

меру варианта.

Для решения заданного уравнения при каждом значении k необходимо произвести реализацию посредством одного из языков программирования высокого уровня, например Pascal, алгоритмов следующих численных методов:

1)метода деления пополам;

2)метода простой итерации;

3)метода Ньютона.

Эти же решения необходимо определить, используя один из встроенных методов поиска табличного процессора Microsoft Excel.

Обработка и сравнение результатов решений выполняются при помощи Microsoft Excel. Оформление итогового отчета по выполнению работы производится в текстовом редакторе Microsoft Word.

169

elib.pstu.ru

4.2.Порядок решения

4.2.1.Выбор исходного капиталовложения x0

В качестве исходного капиталовложения x0 можно взять любое ненулевой значение из области определения функции z f x . Например, если задана функция z x2 , то исходное

капиталовложение выбирается из всего ряда действительных чисел. Пусть x0 2 . Далее производится расчет исходной при-

были при заданном капиталовложении z0 f x0 . Для нашего примера получаем z0 x02 22 4 .

4.2.2. Расчет ряда необходимых сезонных значений прибыли

Предполагая дальнейший рост или уменьшение прибыли предприятия на 10% за сезон, создаем ряд необходимых сезонных значений прибыли, состоящий из n 1 чисел (с учетом исходного данного z0 ). Применительно к нашей исходной прибы-

ли z0 4 и n 10 получаем значения, приведенные в табл. 4.1.

Таблица 4.1 Ряд необходимых сезонных значений прибыли

4.2.3. Расчет сезонных значений капиталовложений

Для вычисления значений капиталовложения, позволяющего получить заданную прибыль за рассматриваемый сезон, не-

обходимо разрешить уравнение zk f x . Решение данного уравнения производится последовательно для каждого сезона

170

elib.pstu.ru