284

горитму подбирает в изменяемых ячейках такие значения, которые приводят к необходимому результату в целевой ячейке. Исходов значения целевой ячейки всего три. Для них в окне Поиск решения после слова Равной: приводятся радиокнопки: мак-

симальному значению, минимальному значению и значе-

нию: (см. рис. 2.66). После последней радиокнопки идет поле,

вкотором можно указать то значение, которому должна быть

врезультате решения равна целевая ячейка. Обычно это значение выбирается равным нулю. Если поле с целевой ячейкой не указано, то не имеет значения, какая радиокнопка отмечена. В этом случае для полноценной постановки задачи необходимо указать ограничения.

Рис. 2.67. Добавление ограничений

В большинстве задач существуют ограничения на изменяемые ячейки. Например, при решении целочисленных задач подбираемые значения обязательно должны быть только целыми числами. Для установки ограничений в окне Поиск решения отводится поле Ограничения:. Работать с ограничениями можно только через специально отведенные для этого кнопки: До-

бавить, Изменить, Удалить (см. рис. 2.66). При добавлении ограничений появляется новое диалоговое окно (рис. 2.67). Здесь, в поле Ссылка на ячейку:, нужно указать ячейку или диапазон ячеек, значения в которых нужно ограничить. Затем в поле Ограничение: нужно либо указать вручную, либо выбрать ячейку или диапазон ячеек со значением ограничений. В центральном поле выбирается знак ограничения. Например,

151

elib.pstu.ru

можно написать: A5 <= 5, или A5 >= B5. При выборе целочисленного или двоичного ограничений значение ограничения писать не нужно. Ограничение двоичности указывает на то, что ограниченная ячейка может принимать значения 0 или 1. Чтобы ограничение появилось в поле Ограничения: окна Поиск ре-

шения, нужно в окне Добавить ограничения нажать клавишу

ОК (см. рис. 2.67). Если будет нажата клавиша Добавить, то пользователю предложат добавить еще одно ограничение. Иногда это сбивает с толку, поэтому советуем добавлять ограничения последовательно, используя клавишу ОК.

Рис. 2.68. Установка параметров поиска решения

После выбора всех необходимых ячеек и ограничений можно производить поиск решения. Для этого используют клавишу Выполнить (см. рис. 2.66). В редких случаях, при плохих результатах расчетов, можно обратиться к параметрам поиска. Окно с параметрами приводится на рис. 2.68. Максимальное время и предельное число итераций можно не изменять. Вместо этого следует выполнить поиск решения несколько раз подряд, используя в качестве первого приближения последний результат поиска.

152

elib.pstu.ru

Заметим, что первое приближение играет очень важную роль при отыскании решения. Если оставить изменяемые ячейки пустыми, то они по умолчанию будут содержать нулевое значение, что может не соответствовать ограничениям задачи. Начальное значение изменяемых ячеек лучше всего задавать с учетом ограничений и смысла задачи. Плохой выбор начального значения может привести к отрицательному результату поиска или к нежелательному результату. Кроме того, если решений задачи много, то при различных начальных значениях могут быть найдены различные решения. Очень важно учитывать эту ситуацию при анализе.

Обратим внимание на следующий факт. Параметры поиска

относительная погрешность и сходимость заданы с разделени-

ем целой и дробной части через запятую. Если установить в MS Excel в качестве разделителя точку, то эти параметры поиска будут неправильно рассмотрены. Поэтому советуем не использовать в MS Excel в качестве разделителя целой и дробной части точку, особенно при выполнении поиска решения.

В случае решения линейных задач, то есть задач, у которых целевая ячейка и ограничения линейно зависят от изменяемых ячеек, в параметрах поиска желательно ставить галочку на пункте Линейная модель (см. рис.2.68). Иногда необходимо отслеживать результаты поиска после каждой итерации, каждого шага. Например, для оценки погрешности и сходимости решения. Для этого в параметрах поиска нужно поставить галочку рядом с пунктом Показывать результаты итераций

(см. рис. 2.68). Если решение задачи так и не удается найти, то можно попробовать изменить метод поиска. В MS Excel встроено два метода: метод Ньютона и метод сопряженных градиентов (см. рис. 2.68). Другие параметры поиска можно оставить по умолчанию.

При выполнении поиска решения возможны два варианта исхода: решение было найдено и решение не было найдено. В обоих случаях пользователю предоставляется оповещение

153

elib.pstu.ru

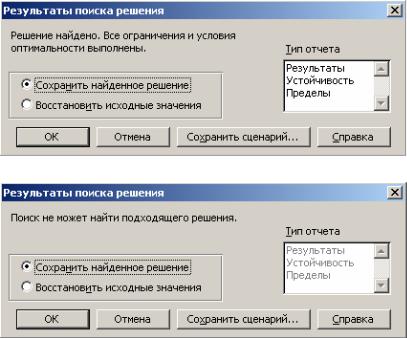
в виде диалогового окна Результаты поиска решения

(рис. 2.69). Не нужно игнорировать это оповещение, а нужно внимательно читать его содержание. При поиске решения в изменяемых ячейках перебираются различные варианты значений, и в конечном счете остается последний вариант. Однако числа, указанные в изменяемых ячейках, далеко не всегда будут являться решением задачи. Именно для этого служит окно Результаты поиска решения. Только в нем четко указывается информация об успешности выполнения поиска.

а

б

Рис. 2.69. Результаты поиска решения:

а – решение найдено; б – решение не найдено

Если решение не было найдено, то можно сохранить последний вариант значений поиска и выполнить поиск решения

154

elib.pstu.ru

еще раз. Это может помочь в том случае, если для поиска решения недостаточно итераций или времени, которые указаны в параметрах поиска (см. рис. 2.68). При удачном поиске решения необходимо сохранить результат. В этом случае значения в изменяемых ячейках и целевой ячейке будут соответствовать решению. Кроме того, можно вывести отчет о поиске решения, выбрав один или несколько пунктов в поле Тип отчета (см. рис. 2.69, а). Отчет выдается в новом отдельном листе книги MS Excel и имеет интерес только для опытных специалистов. Для упрощения получения решения задачи советуем всегда сохранять найденное решение и не выводить никаких отчетов.

155

elib.pstu.ru

3. ЧИСЛЕННЫЕ МЕТОДЫ ОТЫСКАНИЯ КОРНЯ УРАВНЕНИЯ

Рассмотрим несколько численных методов, позволяющих отыскать решение некоторого нелинейного уравнения.

Пусть имеется нелинейное уравнение

Требуется найти корни этого уравнения, т.е. значения x, которые обращают уравнение (3.1) в тождество. Численный процесс приближенного решения поставленной задачи разделяют на два этапа: отделение корня и уточнение корня.

Для отделения корня необходимо определить промежуток аргумента x, где содержится один и только один корень уравнения. Одна из точек этого промежутка принимается за начальное приближение корня. В зависимости от метода, который предполагается использовать для уточнения корня, требуется определение некоторых свойств отделенного корня и поведения функции на отрезке отделения. Например, при использовании метода деления пополам необходимо и достаточно установить лишь непрерывность функции на отрезке отделения.

Этап отделения корня уравнения алгоритмизирован только для некоторых классов уравнений (наиболее известным из которых является класс алгебраических уравнений), поэтому отделение корней нелинейных уравнений обычно выполняется «вручную» с использованием всей возможной информации

о функции F x . В ряде случаев отделение корня может быть

произведено из физических соображений, если речь идет о решении нелинейного уравнения, связанного с конкретной прикладной задачей. Часто применяется графический метод отделения действительных корней, обладающий большой наглядностью.

156

elib.pstu.ru

В ряде случаев может быть полезной теорема, известная из курса математического анализа.

ТЕОРЕМА: Если непрерывная на a;b функция F x , определяющая уравнение (1), на концах отрезка a;b принимает значения разных знаков, то есть F a F b 0 , то на этом отрезке содержится по крайней мере один корень уравнения. Если же функция F x непрерывна и дифференцируема и ее производная сохраняет знак внутри отрезка a;b , то на этом отрезке находится только один корень уравнения.

Вслучае когда на концах интервала функция имеет одинаковые знаки, на этом интервале корни либо отсутствуют, либо их четное число.

На этапе уточнения при нахождении корня используют два типа методов: прямые и итерационные. В прямых методах корень уравнения может быть найден за конечное, заранее известное число операций. Прямыми методами удается решить некоторые простейшие алгебраические и тригонометрические уравнения.

Витерационных методах корень x определяется как пре-

дел некоторой последовательности x0 , x1 ,…, xk , и решение не

может быть достигнуто за конечное, заранее известное число операций. Говорят, что итерационный процесс сходится, если при стремлении числа итераций к бесконечности найденное значение корня стремится к истинному значению корня:

lim xk x .

k

Основные методы решения нелинейных уравнений и систем являются итерационными, к их числу принадлежат метод деления отрезка пополам (дихотомии), метод простой итерации, метод Ньютона (метод касательных), метод хорд, метод парабол (метод Мюллера), метод Зейделя.

157

elib.pstu.ru

Важной характеристикой итерационных методов является скорость сходимости процесса. Она определяется числом итераций, необходимых для получения решения с заданной точность. Чем меньше совершается итераций и чем больше точность решения, тем выше считается скорость сходимости метода. Нужно отметить, что понятие точности решения является относительным и может определяться по-разному в зависимости от метода, вида уравнения, отрезка, на котором определяется решение или исходя из других соображений.

Помимо скорости сходимости сравнение методов производят по числу операций при реализации одной итерации. Если два метода имеют одинаковую скорость сходимости, то более эффективным считается тот метод, у которого на каждой итерации выполняется меньшее число действий.

3.1. Метод деления отрезка пополам

Пусть задано нелинейное уравнение (3.1). Необходимо найти решение этого уравнения на отрезке x a;b , если известно,

что на этом отрезке функция F x непрерывна и уравнение

имеет только один корень.

Для отыскания решения построим итерационный процесс сужения отрезка a;b так, чтобы корень всегда был расположен внутри получаемого суженного отрезка. Для этого определяем

середину отрезка x0 b 2 a и находим значение функции в этой

точке F x0 . После этого определяем, на каком из двух новых отрезков a; x0 или x0 ;b расположено искомое решение. Для этого составляем произведения F a F x0 и F b F x0 .

Решение будет располагаться на том отрезке, на котором произведение будет отрицательно, т.е. значения функции на краях этого отрезка будут иметь разные знаки. Если же оба произве-

158

elib.pstu.ru

дения будут равны нулю, то точка x0 и будет точным решением уравнения (3.1).

ния, то есть значение правой границы переносится в центр отрезка b x0 . Далее вновь отыскивается середина отрезка

x1 b 2 a , определяется значение функции в полученной точке

F x1 и производится проверка на отрицательность произведений F a F x1 и F b F x1 . Выбирается отрезок, на котором расположено решение a; x1 (см. рис. 3.1), отрезок x1;b

выбрасывается из рассмотрения. Подобные действия производятся до тех пор, пока не будет выполнено условие точности вычисления корня.

y F a

y F x

Рис. 3.1. Иллюстрация метода деления отрезка пополам

159

elib.pstu.ru

Окончание итерационного процесса (выполнение условия точности) для данного метода будет заключаться в выполнении одного из следующих условий:

условия близости границ рассматриваемого интервала: b a 2 ;

условия близости значений корня для двух последовательных приближений: xk xk 1 ;

условия близости значения функции в точке xk к нулю:

F xk .

Параметр задается и является мерой точности определения корня уравнения. Первые два условия для метода деления отрезка пополам равнозначны.

Рассмотренный метод прост и надежен, всегда сходится, хотя и не быстро, устойчив к ошибкам округления. К сожалению, не обобщается на системы уравнений.

3.2. Метод простой итерации

Для отыскания корня уравнения (3.1) на отрезке x a;b

методом простой итерации необходимо исходное уравнение заменить эквивалентным уравнением следующего вида:

Примем некоторое начальное значение x x0 . Подставляя

это значение в правую часть уравнения (3.2), получаем новое приближение

x1 f x0 .

Таким образом, выстраивается итерационный процесс для отыскания решения в виде последовательного вычисления зна-

чений функции f x :

xk f xk 1 .

160

elib.pstu.ru