Строительная механика стержневых систем. Часть 1

Построим л. в. RD (см. рис. 3.17, б). Груз P = 1 на консоли с опорой D. Линию влияния RD см. на рис. 3.9. Далее груз P = 1 на балке Ш2Ш3 , давление на консоль с опорой D передается через шарнир (опору) Ш3. Если груз P = 1 на опоре Ш3 , это равносильно тому, что груз P = 1 на конце консоли с опорой D. В этом случае RD = 1. Груз P = 1 на опоре Ш2 , тогда Rш3 = 0 , и следова-

тельно, RD = 0. Отложим нулевую ординату под грузом, т.е. на вертикали шарнира Ш2 . Соединяем точку с ординатой +1 и нулевую точку, соответствующую шарниру Ш2 . Когда груз P = 1 в пределах балок АШ1 и ВС, давление на консоль с опорой D не

передается.

Рассмотрим построение линий влияния поперечных сил и изгибающих моментов в сечениях K1 , K2 , K3 .

Построим л. в. QKправ1 (см. рис. 3.17, в). Сечение K1 считаем

отстоящим на бесконечно малую величину вправо от опоры B. Груз P = 1 перемещаем по балке BC и ее консолям, строим л. в.

QKправ1 в пределах этой балки (см. рис 3.5, б).

Груз на балке АШ1 и ее консоли. С этой балки давление на левую консоль балки BC передается. Если груз P = 1 на опоре Ш1, то это равносильно тому, что P = 1 на конце консоли балки

BC. В этом случае QKправ1 = cl . Если груз P = 1 на опоре А, реакция

RШ1 балки АШ1 равна 0. Тогда и QKправ1 = 0. Под грузом от оси откладываем ординату, равную 0. Соединяем две точки (с ординатой cl и 0) прямой и продолжаем ее на левую консоль балки

АШ1 .

Перемещаем груз P = 1 по балке Ш2Ш3. Давление с этой балки на правую консоль балки BC передается через шарнир

41

натами – dl и 0).

Груз P = 1 на консоли с опорой D. С этой балки давление на балку Ш2Ш3 не передается, следовательно, не передается и на бал-

аналогично.

3.9. Задачи для самоконтроля

Задача 3.4. Проверить балку на геометрическую неизменяемость (размеры указаны в метрах):

сунке задачи 3.4 по линиям влияния, предварительно построив поэтажную схему.

Ответы:

Задача 3.4: балка геометрически неизменяемая.

ГЛАВА 4. РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ ПЛОСКИХ ФЕРМ

4.1. Понятие фермы. Классификация ферм

Фермой называется стержневая система, в расчетной схеме которой жесткие узлы заменены шарнирами. Ферма используется в качестве перекрытий, в мостовых конструкциях.

Элементы фермы, расположенные по контуру, образуют пояса. Различают верхний пояс и нижний пояс. Стержни фермы называют по обозначению узлов (рис. 4.1).

Рис. 4.1

Стержни верхнего пояса: 2–4, 4–6, 6–8, 8–10, 10–12, 12–14. Стержни нижнего пояса: 1–3, 3–5, 5–7, 7–9, 9–11, 11–13.

Стержни, соединяющие пояса, образуют решетку:

–вертикальные стержни – стойки: 1–2, 3–4, 5–6, 7–8, 9–10, 11–12, 13–14;

–наклонные стержни – раскосы: 2–3, 4–5, 6–7, 8–9, 10–11,

12–13.

Вферме нагрузка передается через узлы (в дальнейшем рассматриваем только узловую нагрузку) и все стержни работают только на продольные усилия (растяжение или сжатие). Рас-

тяжение принимаем со знаком «+», сжатие со знаком « ». Расстояние между соседними узлами по горизонтали

называют панелью и обозначают d (см. рис. 4.1). Фермы классифицируют:

43

1)по очертанию поясов (с параллельными поясами, трапециевидные, треугольные, с ломаным, круговым или параболическим поясами);

2)очертанию решетки (с треугольной решеткой, с ромбической решеткой, раскосные, полураскосные, многораскосные);

3)назначению (стропильные, мостовые, башенные);

4)опиранию (балочные, консольно-балочные, консоль-

ные).

4.2. Проверка геометрической неизменяемости фермы

Число степеней свободы плоской фермы определяем по формуле

W = 2y – (Cф + Cоп ),

где y – число узлов, в том числе опорных; Cф – число стержней фермы;

Cоп – число опорных стержней.

Проверка геометрической неизменяемости выполняется по правилам присоединения узлов или дисков к геометрически неизменяемому диску (первоначально – к шарнирному треугольнику). Рассмотрим, например, ферму на рис. 4.2.

Рис. 4.2

Определяем степень подвижности (число степеней свободы): W 2 14 – (25 3) 0 – это необходимое условие.

Используем правила геометрической неизменяемости. Шарнирный треугольник 5–7–8 геометрически неизменяемый.

44

К нему присоединяем узел 6 при помощи стержней 5–6 и 6–8, не лежащих на одной прямой. Следовательно, образовавшаяся система геометрически неизменяемая (см. гл. 1). Иначе к шарнирному треугольнику 5–7–8, который можно рассматривать как диск, присоединяем два диска (стержня) 5–6

и6–8. Три диска соединены тремя шарнирами 5, 6 и 8, не лежащими на одной прямой (правило 4, см. гл. 1). Принимаем теперь эту систему за один диск. К нему присоединяем узел 3 стержнями 3–8 и 3–5, не лежащими на одной прямой (можно использовать правило соединения трех дисков). Получаем геометрически неизменяемую систему, к которой присоединяем узел 4 стержнями 3–4 и 4–6. Затем присоединяем узел 1 стержнями 1–8 и 1–3, не лежащими на одной прямой. Дальше присоединяем узел 2 стержнями 2–1 и 2–4.

Рассуждая аналогично, присоединяем узлы 9, 10, 11, 12, 13

и14. Заданная ферма геометрически неизменяемая и прикреплена к массиву при помощи трех опорных стержней, не пересекающихся в одной точке и не параллельных друг другу. Значит, сооружение геометрически неизменяемое.

4.3. Определение усилий в стержнях простейших ферм от неподвижной нагрузки

Для определения усилий в стержнях простейших ферм от неподвижной нагрузки в первую очередь находят реакции опор фермы, так же как и в балках (простых, консольных).

Затем ферму рассекают сечением на две части и рассматривают равновесие одной из частей, приняв усилия в рассеченных стержнях растягивающими (положительными), т.е. направленными от узла. Усилия в стержнях верхнего пояса будем обозначать буквой О, например усилие в стержне 2–4 (см. рис. 4.1 и

4.2) – О2–4 . В остальных стержнях верхнего пояса – О4–6 , О6–8 ,

О8–10 , О10–12 , О12–14 . Усилия в стержнях нижнего пояса обозначаем как U. Тогда имеем усилия U1–3 , U3–5 , U5–7 , U7–9 , U9–11 ,

U11–13.

45

Усилия в стойках обозначим как V, в раскосах – D. Соответственно усилия в этих стержнях: V1–2 , V3–4 , V5–6 , V7–8 , V9–10 ,

так, чтобы в него входило одно неизвестное интересующее нас усилие. Отсюда два способа определения усилий:

1)способ моментной точки,

2)способ проекций.

Способ проекций применяется в двух вариантах. Первый вариант способа проекций – когда все усилия, образовавшиеся сечением, кроме рассматриваемого, параллельны. Второй вариант способа проекций применяется, когда рассматривается равновесие узла.

4.3.1. Определение усилий в стержнях ферм способом моментной точки (способ Риттера)

Рассмотрим ферму на рис. 4.3.

Рис. 4.3

Нагрузка в пролете симметричная, следовательно, вертикальные реакции опор равны, т.е. RA = RB = 2P = 2P.

46

Найдем усилия в стержнях 4–6 и 3–6, т.е. О4–6 и D3–6 .

Проведем сечение I–I. Усилия в рассеченных стержнях принимаем растягивающими.

Рассмотрим равновесие левой части фермы, образованной сечением I–I. Для определения усилия О4–6 рационально взять

M относительно точки 3, так как два не интересующих нас

усилия, образовавшихся сечением I–I, пересекаются в т. 3 и, следовательно, относительно этой точки момента не образуют.

Точка 3 для усилия О4–6 называется моментной (точкой Риттера). Итак, M3левI–I = 0. Это краткая форма уравнения равнове-

то, что стержень 4–6 работает на сжатие.

Определим усилие D3–6 . Два не интересующих нас усилия О4–6 и U3–5 пересекаются в точке O. Точка О – моментная для

Отсюда D3 6 = Pd 0,5 Pa . r2

Величины а, r1 и r2 находим с использованием геометрии фермы (см. рис. 4.3):

47

где S – длина отрезка.

Простейшая форма способа моментной точки – когда в сечение попадает не более трех стержней фермы.

Примечание: далее в узлах ферм шарниры не изображены, но они подразумеваются и в расчетах учтены.

4.3.2. Определение усилий в стержнях фермы способом проекций

Обратимся к 1-му варианту использования способа проекций. Рассмотрим ферму на рис. 4.4.

Рис. 4.4

Найдем усилие V5–6 . Реакции опор RA RB 3P. Рассечем

ферму сечением I–I на две части так, чтобы в сечение обязательно попал стержень 5–6, при этом количество стержней должно быть наименьшим. Два не интересующих нас стержня 6–8 и 3–5 параллельны. Составим уравнение равновесия сил ле-

вой части фермы: Y левI–I = 0, т.е.

48

V5–6 + P + P P2 RA = 0, отсюда V5–6 = 0,5P . Усилия О6–8 и

U3–5 проекции на вертикальную ось Y не дадут.

Найдем усилие D8–9 . Используем сечение II–II. Рассмотрим равновесие правой части фермы Y правII–II = 0,

D8–9 cos + RB P P P2 = 0, отсюда D8–9 = 0,5cosP .

Рассмотрим 2-й вариант способа проекций (способ выреза-

ния узлов). Дана ферма (рис. 4.5):

Рис. 4.5

Реакции опор RA RB 2P.

Для определения усилия O1–2 и U1–3 вырезаем узел 1. При

этом ферма разбивается также на две части. Левая часть – узел 1 (рис. 4.6).

Рис. 4.6

49

Составляем уравнения равновесия всех сил узла 1 так, чтобы в уравнение входило только одно неизвестное интересующее нас усилие. Тогда для определения O1–2 берем проекцию всех

сил узла 1 на ось, перпендикулярную U1–3 (ось y), а для определения U1–3 проектируем все силы на ось перпендикулярную

усилию O1–2 , т.е. ось z. у = 0 ; О1– 2 sin + RA P2 = 0 .

Отсюда О1–2 = 1,5 P . sin

z = 0, U1–3 sin + ( P2 RA )cos = 0.

Отсюда U1–3 = 1,5 P cos = 1,5 P ctg . sin

Простейшая форма равновесия узла – случай, когда в узле сходится не более двух стержней.

4.3.3.Частные случаи равновесия узлов

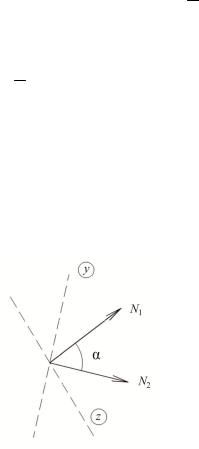
1.В двухстержневом узле без нагрузки усилия в стержнях равны нулю (рис. 4.7).