
Оптическое материаловедение
..pdf
При присоединении третьего атома к двухатомной молекуле происходит расщепление единственного колебательного уровня с собственной частотой ω0 на два, с частотами несколько меньше и несколько больше собственной частоты исходного уровня двухатомного мономера.
Продолжение наращивания числа мономеров в цепочке ведет к дальнейшему последовательному расщеплению колебательных уровней, причем различия между частотами соседних уровней уменьшаются.
В линейной цепочке с числом атомов N порядка числа Авогадро вместо единственного колебания с частотой ω0 возникает квазинепрерывная колебательная зона с квазибесконечным числом колебательных состояний, заключенных в конечном интервале частот от ω1 = ω0 – ∆ω до ω2 = ω0 + ∆ω, где ∆ω − полуширина этой зоны.
Для квазибесконечных упорядоченных структур (кристаллы) существует правило отбора по трансляционной симметрии, согласно которому только состояние, лежащее на краю колебательной зоны, способно воспринять энергию кванта излучения.
31

3.6. Фундаментальные колебательные возбуждения в твердых телах

 Колебательное возбуждение в твердом теле носит название фонон.
Колебательное возбуждение в твердом теле носит название фонон. 

В кристалле фонон представляет собой делокализованное состояние в виде плоской волны возбуждения, пробегающей через всю его решетку.
В простейшем случае ионных кристаллов фонон представляет собой колебательное движение катионной подрешетки как целого относительно анионной подрешетки.
В трехмерной структуре кристалла возникает (3N − 3) колебаний, которые образуют различные колебательные зоны.
Число и взаимное расположение колебательных зон (и соответствующих краям этих зон полос поглощения) определяются симметрией кристаллической решетки и симметрией взаимного расположения атомов в элементарной ячейке кристалла.
Для кристаллов с особо сложными элементарными ячейками общее число полос фундаментальных колебаний в их спектрах может достигать нескольких десятков.
Кубические кристаллы характеризуются высокой степенью изотропности свойств, а потому для них существует только одна собственная фононная частота ω0, которой соответствует мощная полоса поглощения в среднем или дальнем ИК-диапазоне.
Интенсивность любого колебательного возбуждения зависит от величины изменения дипольного момента атомной группы или молекулы в процессе колебательного движения.
Существуют виды колебаний, при которых дипольный момент остается постоянным (меняется лишь поляризуемость). Такие колебания не могут возбуждаться ИК-излучением и, соответственно, не могут давать полос поглощения в ИК-спектре.
32

Спектры оптических постоянных стеклообразного SiO2 в ИК-диапазоне
В стеклах и других неупорядоченных материалах отменяется правило отбора по трансляционной симметрии.
Фононы в неупорядоченных структурах локализованы в областях микроскопических размеров.
33

3.7.Многофононное поглощение
Сдостаточно малой вероятностью поглощение ИК-излучения может происходить и при частотах, не совпадающих с частотой фундаментального колебания.
Примерно кратные частоты ка- кого-либо фундаментального ко-
лебания – обертоны.
Первый, второй и так далее обертоны фундаментального колебания с частотой ω01 примерно соответствуют удвоенной, утроенной и так далее частоте этого колебания.
Сумма двух или более частот различных фундаментальных колебаний –
составные частоты.
Составные частоты могут обозна-
чаться как ω01 + ω02, 2ω01 + ω02,
ω01 + 2ω02 и т.д.
Многофононные спектры или колебательные спектры второго, третьего и так далее порядка.
Точные значения частот обертонов оказываются немного ниже за счет влияния ангармонизма.
34

Лекция 4. ОПТИКА МАТЕРИАЛА В ДИАПАЗОНЕ ПРОЗРАЧНОСТИ
Явление вариации оптических постоянных с длиной волны или частотой в оптике обозначается термином «дисперсия» – частотная или волновая дисперсия.
В области прозрачности показатель преломления нелинейно уменьшается с длиной волны –
«нормальная» дисперсия.
За пределами области «нормальной» дисперсии по обе ее стороны лежат области, в которых показатель преломления возрастает с длиной волны – области «аномальной» дисперсии.
Полный спектр оптических постоянных стеклообразного кремнезема
Положение мощных максимумов собственного поглощения как раз и соответствует центрам областей «аномальной» дисперсии.
35

При отсутствии поглощающих примесей и собственных дефектов потери света в бесцветных оптических материалах определяются лишь «хвостами» областей собственного электронного и колебательного поглощения, расположенными в вакуумном УФ- и среднем ИК-диапазонах.
Для кварцевого стекла известно, что точка пересечения этих «хвостов» (и соответственно, точка максимально возможного светопропускания) лежит при длине волны около 1,5 мкм.
а
б
Зависимость показателя преломления n(λ) от длины волны для кварцевого стекла (а) и халькогенидного стекла ИКС25 (б)
36

4.1. Соотношения Крамерса – Кронига
Действительные и мнимые части комплексной диэлектрической проницаемости и комплексного показателя преломления описываются интегральными соотношениями Крамерса – Кронига на основе теоремы Боде:
|
2 ∞ ω*ε"(ω*) |
|
|
2 ∞ ω*κ(ω*) |
|
|||
ε'(ω)=1+ |
|
∫0 ω*2 −ω2 |
dω*; |
n(ω)=1+ |
|
∫0 ω*2 −ω2 d |
ω*; |
|
π |
π |
|||||||
|
ω |
∞ ε'(ω*)−1 |
|
ω∞ n(ω*)−1 |
|
|||
ε"(ω)=−2π |
∫0 [ω*2 −ω2 |
]dω*; |
κ(ω)=−2π ∫0 [ω*2 −ω2 ]dω*, |
|||||
где ω – текущая частота, для которой производится вычисление значения оптической постоянной или функции; ω* – частота, которая служит переменной интегрирования.
Соотношение Крамерса – Кронига для фазового угла ψ(ω) используется для вычисления спектров оптических постоянных из экспериментальных данных об энергетическом коэффициенте отражения:
ω∞ lnR(ω*)
ψ(ω)=−π∫0 ω*2 −ω2 dω*.
носят общий характер и никак не связаны с составом и структурой каких-либо конкретных веществ,
|
|
|
|
|
|
Соотношения |
|
|
применимы к веществам любого состава и в любых |
|
Крамерса – Кронига |
|
|
агрегатных состояниях, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определяют численное значение одной оптической |
|
|
|
|
постоянной или функции через полный спектр вто- |
|
|
|
|
рой оптической постоянной или функции от нуля до |
|
|
|
|
бесконечности. |
|
|
|
|
|
37

4.2. Частотная зависимость оптических постоянных
Первой аналитической моделью дисперсии показателя преломления была формула Зелльмейера, выведенная еще в 1871 г. из физических представлений о мировом эфире.
n2 (λ)−1= ∑J Ajλ2 ,
j=1λ2 −λ2j
где n(λ) – показатель преломления при длине волны λ; Aj – константы материала; λj – эффективные дисперсионные длины волн.
Замена длин волн на частоты позволяет связать дисперсию показателя преломления с физическими процессами взаимодействия электромагнитной волны с веществом:
J |
A ω |
2 |
|
J |
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|||
n2 (ω)−1=∑ |
|
j j |
|
=∑ |
|
|
j |
|
, |
|
2 |
−ω |
2 |
2 |
−ω |
2 |
|||||
j=1 |
ω |
|
j=1 |
ω |
|
|
||||
j |
|
|
|
j |
|
|
|
|
||
где S j – константы, имеющие смысл |
интенсивностей оптических переходов, |
|||||||||
S j =Ajω2j . |
|
|
|
|
|
|
|
|
|
|
Формула Зелльмейера
Достоинства |
|
Недостатки |
|
|
В отличие от соотношений Крамерса – |
Пригодна |
лишь |
в области, |
где |
Кронига представляет дисперсию показа- |
λ > λj и (для части членов суммы) |
|||
теля преломления (его зависимость от |
λ < λj, так как в точках λ = λj правая |
|||
длины волны или частоты) в явном виде – |
часть уравнения имеет разрывы, |
|||
с помощью вполне конкретной матема- |
где показатель преломления обра- |
|||
тической функции текущей длины волны |
щается в бесконечность |
|
||
или частоты |
|
|
|
|
Постоянные параметры Aj и λj могут быть |
Является |
сильно |
упрощенной |
и |
вычислены из эксперимента, после чего |
никак не учитывает связь между |
|||
формула Зелльмейера становится при- |
преломлением и поглощением, от- |
|||
годной для вычисления показателя пре- |
раженную в соотношениях Кра- |
|||
ломления при различных длинах волн |
мерса – Кронига |
|
|
|
38

Лекция 5. ОПТИКА МАТЕРИАЛА В ДИАПАЗОНЕ ПРОЗРАЧНОСТИ (продолжение)
5.1.Аналитическая модель дисперсии диэлектрической проницаемости
вприближении отсутствия локального поля (модель Друде)
Основополагающей идеей классической теории дисперсии явилось рассмотрение смещений связанного электрона по аналогии с колебаниями механического гармонического осциллятора Ньютона.
|
|
|
d 2 x |
dx |
|
Уравнение движения такого осцил- |
|
||
|
лятора имеет вид |
|
m dt 2 |
=qe E −kx−b dt . |
|
|
|
|
|
В правой части этого уравнения первое слагаемое – вынуждающая сила действия электрического поля электромагнитной волны; второе слагаемое – линейная возвращающая сила связи электрона с ядром; третье слагаемое – диссипативная сила.
|
|
|
|
|
|
|
|
|
Решение этого уравнения может быть пред- |
|
|
(qe |
m)E |
|
|
|
ставлено в виде |
|
|
||||
|
|
x =ω02 |
−ω2 −iγω, |
||||
|
|
|
|||||
|
|
|
|||||
где ω02 – собственная частота электронного осциллятора, ω02 =k m ; γ – коэффициент затухания электронного осциллятора, γ=b
m ; γ – коэффициент затухания электронного осциллятора, γ=b m .
m .
На основе решения этого уравнения можно вычислить наведенный дипольный момент и через него – модуль вектора поляризации вещества, а затем и диэлектрическую проницаемость:
x = |
(qe m)E |
||
ω02 |
−ω2 −iγω |
||
|
|||
ε0ε%Er=ε0 Er+Pr
P |
=N |
q |
x = |
qe2 Nq |
|
|
1 |
E |
, |
|
|||
|
m |
ω02 |
−ω2 −iγω |
|
|||||||||
x |
q |
e |
|
|
|
x |
|
|
|||||
|
′ ′′ |
|
|
P |
|
|
|
ω2p |
|
|
|
||
% |
|
|
x |
|
|
|
|
|
|
|
|
||
|
|
ε0 E |
=1+ω02 −ω2 −iγω. |
||||||||||
ε=ε +iε =1+ |
|||||||||||||
39
Диэлектрическая проницаемость для набора из J-осцилляторов, представляющих собой связанные электроны в веществе, будет иметь вид
J |
|
2 |
|
ε=1+∑ |
2 2 |
, |
|
% |
|
ωpj |
|
ω |
−ω −iγω |
|
|
= |
|
||
j 1 |
j |
|
|
где ω2p |
– константа, называемая плазменной частотой, |
ω2p |
= Nqe2 |
; (N – плотность ос- |
|
|
|
mε0 |
|
цилляторов); ωрj и ωj – плазменные и собственные частоты различных электронных осцилляторов.
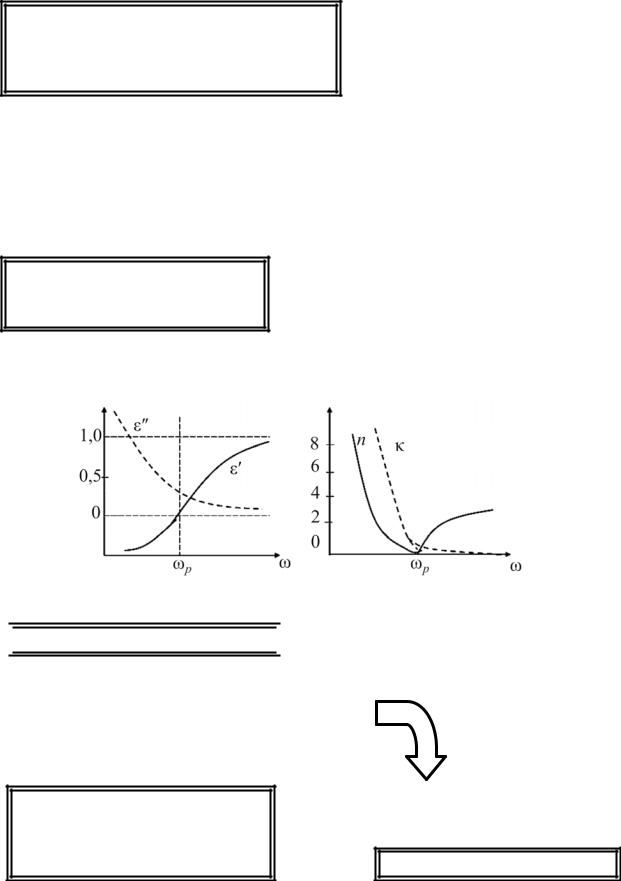
Действительная и мнимая части комплексной диэлектрической проницаемости имеют вид

 В области прозрачности κ(ω) ≈ 0.
В области прозрачности κ(ω) ≈ 0. 

ε"(ω)=2n(ω)κ(ω)≈0 ε(ω)≈ε'(ω)≈n |
(ω) |
|||||
|
|
|
|
% |
2 |
|
|
ω2 −ω2 |
|
>>γ ω |
|
|
|
|
|
|
||||
|
|
|
|
|||
|
j |
|
j |
|
|
|
|
|
|
|
|
||
Формула Зелльмейера является упрощенным частным случаем классической модели Друде для области прозрачности.
|
|
J |
|
ω2pj (ω2j −ω2 ) |
|
||||||
ε'=1+∑ |
|
|
|
|
|
|
|
|
; |
||
|
|
|
2 |
+γ2jω2 |
|||||||
|
|
j=1 |
(ω2j −ω2 ) |
|
|||||||
|
|
|
|
ωpj γ jω |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
J |
|
|
2 |
|
|
|
|
|
|
|
ε"=∑ |
|
|
|
|
|
|
|
|
. |
|
|
|
2 |
2 |
2 |
|
2 |
ω |
2 |
|
|||
j=1 |
(ωj |
−ω |
) |
+γ j |
|
|
|
||||
ε(ω)−1≈n |
J |
2 2 |
||
(ω)−1=∑ |
||||
% |
2 |
|
|
S j |
|
j=1 |
ω |
−ω |
|
|
|
|||
|
|
j |
|
|
Формула Зелльмейера
40
