
5576
.pdf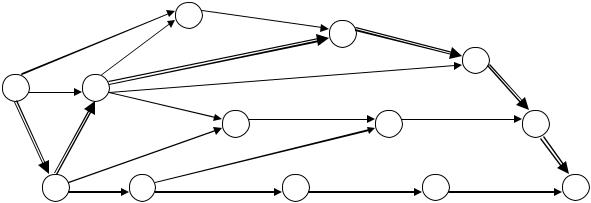
Работа |
|
1 |
– 2 |
1 |
– 3 |
1 |
– 5 |
|
2 |
– 3 |
2 – 4 |
2 – 6 |
|
3 – 5 |
|
3 – 6 |
3 – 8 |
3 – 11 |
(i, j) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tij |
|
|
9 |
|
8 |
|
7 |
|
|
6 |
7 |
5 |
|
2 |
|
6 |
14 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Работа |
|
4 |
– 7 |
4 |
– 9 |
5 |
– 8 |
|
6 |
– 9 |
7 – 10 |
8 – 11 |
|
9 – 12 |
|
10–13 |
11–12 |
12–13 |
(i, j) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tij |
|
|
21 |
|
16 |
|
10 |
|
|
9 |
14 |
2 |
|
12 |
|
6 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Окончательный |
|
вид |
|
сетевого |
графика |
с рассчитанными |
|||||||||||
характеристиками:
–ранними и поздними (в скобках над событиями) сроками свершения событий;
–свободными резервами времени работ (в скобка х рядом с продолжительностями работ) представлен на рисунке 6.8 (проверить самостоятельно):
|
|
|
|
17(19) |
10(2) |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
7(10) |
|
|
|
|
|
8 |
2 |
31 |
|
|
|
|
2(10) |
|
|
14 |
|
|
|
|
|
||
|
|
|
|
|
|
|
11 |
|
|
|||
|
|
15 |
|
|
|
|
7(9) |
|
|
|
|
|
|
8(7) |
|
|
|
|
|
|
|
18 |
|
||
1 |
3 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
6(0) |
21(28) |
9(0) |
30(37) |
12(7) |
|
49 |
|
9 |
6 |
|
|
|
|
6 |
|
9 |
12 |
|||
|
|
|
|
|
|
|
|
|
|
9 |
||
|
|
|
5(7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
16(3) |
|
|
|
|
|
|
||
|
9 |
|
11(17) |
32(38) |
|
|
46(52) |
|
58 |
|||
|
|
|
|
|
|
|
||||||
|
2 |
2(0) |
4 |
|
|
21(0) |
7 |
14(0) |
|
10 |
6(6) |
13 |
Рисунок 6.8 – Сетевой график с рассчитанными характеристиками
Исходные данные для оптимизации и результаты оптимизации представлены в таблице 6.3.
81
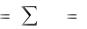
Таблица 6.3 – Результаты частичной оптимизации сетевого графика
Работа |
Продолжительность |
Своб. |
Стоимость |
Коэффициент |
tij(1) – |
Уменьше- |
|||
(i, j) |
работы |
|
резерв |
работы Cij |
изменения |
tij(0) |
ние |
||
|
|
tij(0) |
|
tij(1) |
времени |
|
стоимости hij |
стоимости |
|
|
|
|
|
или FSij |
|||||
|
|
|
|
|
FSij |
|
|
∆Cij |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
(1, |
2) |
9 |
|
13 |
0 |
30 |
|
|
|
(1, |
3) |
8 |
|
14 |
7 |
47 |
2 |
6 |
12 |
(1, |
5) |
7 |
|
15 |
10 |
64 |
3 |
8 |
24 |
(2, |
3) |
6 |
|
10 |
0 |
58 |
|
|
|
(2, |
4) |
2 |
|
4 |
0 |
27 |
|
|
|
(2, |
6) |
5 |
|
13 |
7 |
60 |
4 |
7 |
28 |
(3, |
5) |
2 |
|
3 |
0 |
36 |
|
|
|
(3, |
6) |
6 |
|
9 |
0 |
64 |
|
|
|
(3, |
8) |
14 |
|
26 |
0 |
120 |
|
|
|
(3, 11) |
7 |
|
10 |
9 |
48 |
10 |
3 |
30 |
|
(4, |
7) |
21 |
|
27 |
0 |
72 |
|
|
|
(4, |
9) |
16 |
|
21 |
3 |
74 |
4 |
3 |
12 |
(5, |
8) |
10 |
|
16 |
2 |
68 |
5 |
2 |
10 |
(6, |
9) |
9 |
|
13 |
0 |
63 |
|
|
|
(7, 10) |
14 |
|
19 |
0 |
96 |
|
|
|
|
(8, 11) |
2 |
|
3 |
0 |
43 |
|
|
|
|
(9, 12) |
12 |
|
19 |
7 |
56 |
3 |
7 |
21 |
|
(10, |
13) |
6 |
|
9 |
6 |
28 |
5 |
3 |
15 |
(11, |
12) |
8 |
|
21 |
0 |
62 |
|
|
|
(12, |
13) |
9 |
|
15 |
0 |
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ИТОГО: |
|
|
|
|
1 152 |
|
|
152 |
|
Расчётная часть таблицы заполнена только для работ, имеющих свободный резерв времени, так как продолжительность только этих работ можно увеличить. В таблице подчёркнуты те работы, свободный резерв времени которых полностью исчерпан.
Стоимость первоначального варианта плана равна
С |
Cij 1 152 . |
|
|
(i, j) |
|
Стоимость нового плана равна |
|
|
|
С – ∆С = 1 |
000, |
т.е. уменьшилась на 13,2%.
Продолжительность критического пути равна 58. Новый план имеет вид:
82
Рассчитав временные характеристики полученного сетевого графика, получим, что он содержит пять критических путей (отмечены на графике удвоенными линиями).
83

Глава 7. Элементы теории игр
7.1 Основные понятия теории игр
Теория игр – это теория математических моделей ситуаций, интересы участников которых различны, причём они достигают своей цели различными путями. Столкновение противоположных интересов участников приводит к возникновению конфликтных ситуаций.
Задачей теории игр является выработка рекомендаций по рациональному образу действия участников конфликта.
Игрой называется упрощённая модель конфликтной ситуации. Например, шахматы, шашки, карточные игры – естественная база
для анализа конфликтных ситуаций.
Терминология теории игр: игроки (стороны, участвующие в конфликте), выигрыш (исход конфликта) и т.д.
Игры бывают:
комбинаторные (шахматы);
азартные (кости, рулетка, герб – решка);
 стратегические (источник неопределённости – отсутствие информации о действиях противника).
стратегические (источник неопределённости – отсутствие информации о действиях противника).
Рассмотрим стратегические игры. Стратегические игры бывают парными (два игрока) и множественными. Большое практическое значение имею парные игры. Обозначим участников игры через А и В.
Для каждой формализованной игры вводятся правила, т.е. система условий, определяющая: 1) варианты действий игроков; 2) объём информации каждого игрока о поведении партнёров; 3) выигрыш, к которому приводит каждая совокупность действий. Результат игры (выигрыш) определяется некоторым числом.
Игра называется игрой с нулевой суммой, или антагонистической, если выигрыш одного из игроков равен проигрышу другого. Если обозначить а – выигрыш одного из игроков, b – выигрыш другого, то для игры с нулевой суммой b = – a, поэтому достаточно рассматривать, например, а.
Ходом в теории игр называется выбор и осуществление одного из
84
предусмотренных правилами действий. Ходы могут быть личными и случайными. Личный ход – это сознательный выбор игроком одного из возможных действий (например, ход в шахматной игре). Случайный ход – это случайное выбранное действие (например, выбор карты из перетасованной колоды). В дальнейшем будем рассматривать только личные ходы игроков.
Стратегией игрока называется совокупность правил, определяющих выбор его действий при каждом личном ходе в зависимости от сложившейся ситуации.
Игрок принимает решения по ходу игры. Теоретически можно предположить, что эти решения приняты игроком заранее. Это означает, что игрок выбрал определённую стратегию, которая может быть задана в виде списка правил или программы.
Игра называется конечной, если у каждого игрока имеется конечное число стратегий и бесконечной – в противном случае.
Оптимальной называется стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный выигрыш, когда второй игрок придерживается своей стратегии; или второй игрок должен иметь минимальный проигрыш, если первый придерживается своей стратегии.
Оптимальные стратегии должны удовлетворять условию устойчивости, т.е. любому из игроков должно быть невыгодно отказаться от своей стратегии в этой игре.
Если игра повторяется многократно, то игроков может интересовать не выигрыш и проигрыш в каждой конкретной партии, а средний выигрыш (проигрыш) во всех партиях.
Целью теории игр является определение оптимальной стратегии для каждого игрока.
Важнейшее ограничение теории игр – единственность выигрыша как показателя эффективности, в то время как большинство реальных экономических задач имеет более одного показателя эффективности. Кроме того, в экономике, как правило, возникают задачи, в которых интересы партнёров не обязательно антагонистические.
85
7.2 Платёжная матрица. Нижняя и верхняя цена игры
Рассмотрим парную конечную игру. Пусть игрок А располагает m личными стратегиями А1, А2, ..., Аm, а игрок В имеет n личных стратегий В1, В2, ..., Вn. В этом случае говорят, что игра имеет размерность m х n. В результате выбора игроками любой пары стратегий Аi и Bj (i 1, m; j 1, n ) однозначно определяется исход игры, т.е. выигрыш aij игрока А (положительный или отрицательный) и проигрыш (– aij) игрока В. Предположим, что значения aij известны для любой пары стратегий (Аi; Bj)
|
а11 |
a12 |
a1n |
Матрица Р |
а21 |
a22 |
a2n , элементами которой являются |
|
аm1 |
am2 |
amn |
выигрыши, соответствующие стратегиям Аi и Bj, называется платёжной матрицей или матрицей игры. Общий вид этой матрицы представлен в таблице 7.1.
Таблица 7.1 – Платёжная матрица
Вj |
В1 |
В2 |
... |
Вn |
Аi |
|
|
|
|
|
|
|
|
|
A1 |
a11 |
a12 |
… |
a1n |
|
|
|
|
|
A2 |
a21 |
a22 |
… |
a2n |
|
|
|
|
|
… |
… |
… |
… |
… |
|
|
|
|
|
Am |
am1 |
am2 |
… |
amn |
|
|
|
|
|
Строки этой таблицы соответствуют стратегиям игрока А, а столбцы – стратегиям игрока В.
Пусть игрок А выбирает некоторую стратегию Аi, тогда в наихудшем случае (например, если выбор станет известным игроку В) он получит
наименьший выигрыш i min aij . (7.1) j
Предвидя такую возможность, игрок А должен выбрать такую стратегию, чтобы максимизировать свой минимальный выигрыш.
86
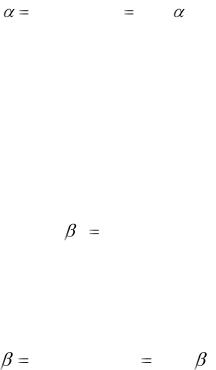
max min aij |
max |
i. |
(7.2) |
|
i |
j |
i |
|
|
Величина α – гарантированный максимальный выигрыш игрока А,
называется нижней ценой игры или максимином.
Стратегия, соответствующая максимуму, называется максиминной стратегией. Игрок В, выбирая стратегию, исходит из следующего: при выборе некоторой стратегии Вj, его проигрыш не превысит максимума из значений элементов j-го столбца матрицы.
j |
max a . |
(7.3) |
|
i |
ij |
|
|
|
|
|
|
Рассматривая множество βj для различных значений j, игрок В выберет такое значение j, при котором его максимальный проигрыш минимизируется.
min |
max aij |
min |
j . |
(7.4) |
j |
i |
j |
|
|
Величина β называется верхней ценой игры, или минимаксом. Это гарантированный минимальный проигрыш игрока В.
Стратегия, соответствующая минимаксу, называется минимаксной
стратегией. |
|
Если α = β = v, |
(7.5) |
то выигрыш игрока А – вполне определённое число, игра называется
вполне определённой, а выигрыш v (7.5) называется ценой игры и равен элементу матрицы, который одновременно является наибольшим в своём столбце и наименьшим в своей строке. Этот элемент называется седловой точкой (по аналогии с поверхностью седла, которая искривляется вверх в
одном направлении и вниз в другом).
Седловой точке соответствуют вполне определённые (чистые) стратегии игроков. Совокупность чистых стратегий А* игрока А и В* игрока В называют решением игры, которое обладает следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то для другого отклонение его от его оптимальной стратегии не может быть выгодно.
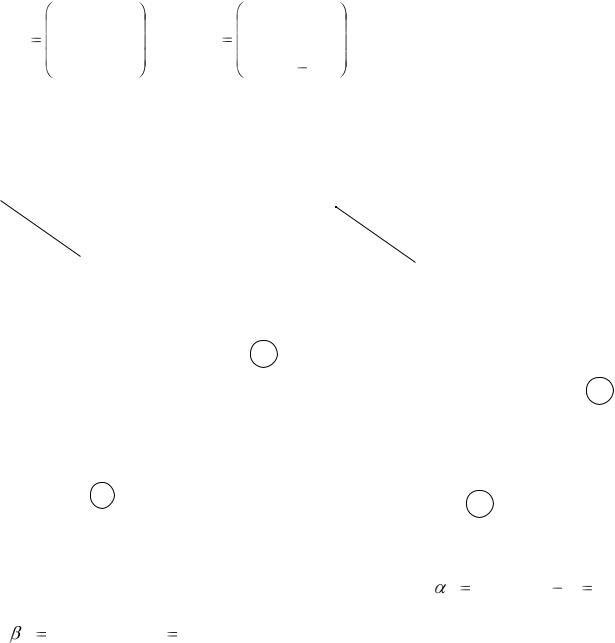
Пример 7.1. Определить нижнюю и верхнюю цены для игр, заданных платёжными матрицами
87
4 |
3 |
4 |
2 |
|
1 |
0 |
3 |
5 |
Р1 3 |
4 |
6 |
5 , |
Р2 |
3 |
2 |
4 |
3 . |
2 |
5 |
1 |
3 |
|
0 |
1 |
1 |
4 |
Решение. Все расчёты удобно проводить в таблице, в которой кроме матрицы Р введены столбец αi и строка βj (табл. 7.2) и (табл. 7.3).
Таблица 7.2 – Платёжная матрица Р1′ Таблица 7.3 – Платёжная матрица Р2′
|
Вj |
В1 |
В2 |
В3 |
В4 |
αi |
Аi |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
4 |
3 |
4 |
2 |
2 |
|
|
|
|
|
|
|
A2 |
|
3 |
4 |
6 |
5 |
3 |
|
|
|
|
|
|
|
A3 |
|
2 |
5 |
1 |
3 |
1 |
|
|
|
|
|
|
|
βj |
|
4 |
5 |
6 |
5 |
|
|
|
|
|
|
|
|
|
Вj |
В1 |
В2 |
В3 |
В4 |
αi |
Аi |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
1 |
0 |
3 |
5 |
0 |
|
|
|
|
|
|
|
A2 |
|
3 |
2 |
4 |
3 |
2 |
|
|
|
|
|
|
|
A3 |
|
0 |
1 |
– 1 |
4 |
–1 |
|
|
|
|
|
|
|
βj |
|
3 |
2 |
4 |
5 |
|
|
|
|
|
|
|
|
Решение. Минимальные значения aij в строках матрицы Р1 равны соответственно (2, 3, 1). Максимальное значение из них равно 3. Следовательно, α1 = 3 – нижняя цена игры. Для определения верхней цены данной матрицы найдём максимальное значение элементов в столбцах матрицы Р1. По столбцам имеем (4, 5, 6, 5). Следовательно, β1 = 4. Поскольку α1 ≠ β1, то матрица Р1 не имеет седловой точки.
|
Аналогично, |
для |
матрицы |
P2 |
2 |
max(0, 2, 1) 2, |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
2 |
min (3, 2, 4, 5) |
2. Таким образом, α1 |
= β2 |
= v = 2 – цена игры. |
||
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение данной игры состоит в выборе игроком А стратегии А2, при этом его выигрыш не меньше 2; для игрока В оптимальной является стратегия В2, позволяющая ограничить его проигрыш этим же числом.
а22 = 2 – седловая точка матрицы Р2. А2, В2 – чистые стратегии игроков А и В соответственно. Отклонение одним из игроков от оптимальной стратегии приводит к уменьшению выигрыша (для игрока А) и увеличению проигрыша (для игрока В).
88

7.3 Решение игр в смешанных стратегиях
Если игра не имеет седловой точки, то применение чистых стратегий не даёт оптимального решения игры. В таком случае можно получить оптимальное решение, случайным образом чередуя чистые стратегии.
Смешанной стратегией SA игрока А называется применение чистых стратегий А1, А2, ..., Аi, ..., Аm с вероятностями р1, р2, ..., рi, ..., pm, причём
m |
|
|
|
|
|
|
|
|
p 1. Смешанные стратегии игрока А записываются в виде матрицы |
||||||||
i |
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
S A |
А1 |
А2 ... |
Аi |
... |
Am , |
|
|
|
|
р1 |
р2 ... |
pi |
... |
pm |
|
|
или в виде строки S A |
( p1, p2 , ..., pi , |
..., |
pm) . |
|
||||
Аналогично для игрока В |
|
|
|
|
|
|
||
SВ |
В |
B ... |
B j |
... |
B |
|
||
1 |
2 |
|
q j |
|
n |
, |
||
|
|
q1 |
q2 ... |
|
... |
qn |
|
|
или SB (q1, q2 , ..., |
q j , |
..., qn) , где |
n |
q j 1. |
|
|||
|
|
|
j |
|
1 |
|
|
|
На основании принципа минимакса определяется оптимальное |
||||||||
решение игры: эта пара оптимальных стратегий S*A, |
SB* в общем случае |
|||||||
смешанных, обладающих следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не выгодно отступать от своей. Выигрыш, соответствующий оптимальному решению, называется ценой игры v. Цена игры удовлетворяет неравенству
α ≤ v ≤ β |
(7.6) |
Справедлива основная теорема теории игр |
– теорема Неймана: |
каждая конечная игра имеет по крайней мере одно оптимальное решение, возможно, среди смешанных стратегий.
Пусть |
* |
* |
* |
* |
* |
* |
* |
, |
* |
SА |
(p1 |
, р2 |
, ..., pm ) |
и SВ |
(q1 |
, q2 |
..., qn ) – пара |
оптимальных стратегий. Если чистая стратегия входит в оптимальную смешанную стратегию с отличной о нуля вероятностью, то она называется
активной.
89
Справедлива теорема об активных стратегиях: если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остаётся неизменным и равным цене игры v, если второй игрок не выходит за пределы своих активных стратегий.
Эта теорема имеет большое практическое значение, она даёт конкретные модели нахождения оптимальных стратегий при отсутствии седловой точки. Чем больше размерность матрицы, не содержащей седловой точки, тем сложнее решение. Поэтому в теории матричных игр рассматриваются способы, с помощью которых решение одних игр сводится к решению других, более простых (в частности с помощью сокращения размерности матрицы). Сократить размерность матрицы можно, исключая дублирующие и заведомо невыгодные доминирующие стратегии. Например, в матрице P2 для игрока В заведомо невыгодной является четвёртая стратегия, так как все значения аi4 превышают соответствующие значения элементов первого и второго столбца. Четвёртый столбец матрицы можно исключить (игрок В не воспользуется этой стратегией).
Можно сократить размер матрицы, разбив её на подматрицы, в которых суммы элементов по столбцам и строкам равны. Тогда вместо чистых стратегий в матрицу включаются смешанные. Элементы сокращённой матрицы получаются делением соответствующих сумм элементов на число чистых стратегий. Если смешанные стратегии входят в число оптимальных, то вероятности использования входящих в них чистых стратегий равны между собой.
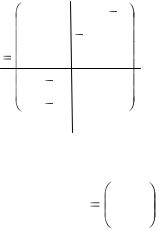
Пример 7.2. Сократить размерность матрицы
2 0 4 2
0 2 2 4 Р3 1 1 1 1
1 1 3 5
1 1 5 3 .
Решение. В матрице P3 для подматриц выполняется условие равенства сумм элементов по строкам и столбцам. Объединяя стратегии
А1 А2 А3; А4 |
А5; В1 В2; В3 |
В4, получим Р3' 1 |
1 . |
|
|
0 |
4 |
90
