5576

длительности обслуживания / число каналов обслуживания): (дисциплина очереди / максимальная длина очереди / ёмкость источника, генерирующего заявки на обслуживание).

Обычно принимаются следующие обозначения для закона распределения входящего потока:

М – пуассоновское (марковский случайный процесс);

Д– детерминированный (с фиксированным интервалом времени между моментами последовательных поступлений заявок в систему);

Еk – Эрланга с параметром k; GI – произвольное.

Для обозначения закона распределения времени обслуживания обозначения следующие:

М – отрицательный экспоненциальный;

Д– детерминированный (с фиксированной продолжительностью обслуживания);

Еk – Эрланга с параметром k;

GS – общее распределение произвольного вида.

Для рассматриваемых далее моделей массового обслуживания дисциплина очереди принимается естественной: первый пришёл, первый обслуживается, и она обычно обозначается FCFS.

Например, обозначения (Д/Д/1) : (FCFS/ / ) означают, что мы имеем дело с моделью массового обслуживания, в которой детерминированный входящий поток, один канал обслуживания, естественная дисциплина очереди, неограниченная длина очереди и неограниченная ёмкость источника заявок. Для теории массового обслуживания подобная модель не представляет интереса и здесь рассматриваться не будет. Кроме того, обычно последний блок обозначений считается стандартным и не указывается; он подключается в случае, если вводятся ограничения либо на длину очереди, либо на ёмкость источника заявок.

Рассмотрим несколько частных стандартных случаев моделей массового обслуживания и приведём формулы для расчёта операционных характеристик таких моделей, имея в виду, что при необходимости эти

111

характеристики могут быть использованы для расчёта стоимостных показателей функционирования систем массового обслуживания и выбора оптимальных стратегий управления этими системами, выбирая уровень обслуживания и издержки системы.

Модель 1. Одноканальная однофазная модель массового обслуживания с пуассоновским входящим потоком и экспоненциальным временем обслуживания (М/М/1).

Предпосылки модели. Одноканальная однофазная модель массового обслуживания с такими характеристиками является одной из наиболее часто используемых и простых моделей. Она является базовой моделью, поэтому рассмотрим её подробно. Обычно она используется при выполнении следующих семи предпосылок:

1)требования обслуживаются в порядке FCFS;

2)каждое требование дожидается обслуживания, несмотря на длину очереди (система массового обслуживания без отказов);

3)требования поступают в систему независимо друг от друга, случайным образом, с известной (фиксированной в среднем) интенсивностью;

4)закон распределения числа требований, прибывающих в систему за единицу времени является пуассоновским и ёмкость источника требований не ограничена (требования поступают из неограниченной совокупности);

5)время обслуживания требований случайное, не меняется от требования к требованию, средняя же интенсивность обслуживания известна;

6)время обслуживания требований подчинено экспоненциальному закону распределения;

7)средняя интенсивность обслуживания больше, чем средняя интенсивность прибытия.

Последнее требование обязательно для устойчивого функционирования системы массового обслуживания ибо, в противном случае, очередь будет неограниченно возрастать.

Обозначим через 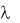среднее (ожидаемое) число требований за

112

единицу времени, а через 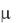– среднюю интенсивность обслуживания. Тогда, при выполнении перечисленных предпосылок имеем:

1) среднее число требований в системе (в очереди, плюс обслуживаемое):

5)коэффициент использования времени обслуживания системы, т.е. вероятность того, что система занята обслуживанием:

=/ ;

6)вероятность простоя системы массового обслуживания, т.е. вероятность того, что в системе нет ни одного требования:

Р0 = 1 – / ;

7) вероятность того, что в системе находится n требований:

Рn = ( / )n (1 – / )

8) вероятность того, что в системе находится не менее k требований:

L = Lq + / = 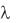W; Wq = W – 1/ = Lq / ; W = Wq + 1/ = L / .

Модель 2. (М/GS/1) – одноканальная однофазная модель массового обслуживания с пуассоновским входящим потоком и произвольным распределением интенсивности обслуживания.

В отличие от предыдущей модели здесь предполагается, что закон распределения времени обслуживания не известен, но известно среднее

113

пуассоновским входящим потоком и фиксированным временем обслуживания. От предыдущей модели эта модель отличается лишь тем, что для неё = 0.

Модель 4. (М/Еk/1) – одноканальная однофазная модель массового обслуживания с пуассоновским входящим потоком и выходящим потоком

Не следует забывать, что, как это было указано при обсуждении закона распределения Эрланга, время обслуживания для каждой фазы считается одинаковым, а общее время обслуживания в системе кратно числу фаз. Например, если время обслуживания для каждой фазы равно 10 минут, а число фаз k = 3, то общее время обслуживания равно 30 минут, т.е. интенсивность обслуживания в среднем равна двум требованиям в час

(т.е. = 2).

Модель 5. (M/M/1) : (FCFS /m/ ). От модели 1 эту модель отличает то, что здесь введены ограничения на длину очереди: m – максимальное число требований в системе, следовательно, если в системе занято все m мест, то очередное требование покинет систему не обслуженным. Такая система массового обслуживания называется системой с отказами. Операционные характеристики такой системы определятся из соотношений:

114

Рm – вероятность того, что требование покинет систему необслуженным.

Модель 6. (М/М/1):(FCFS/ /m). В этой модели в отличие от модели 1 предполагается, что ёмкость источника заявок ограничена величиной m. Такие системы массового обслуживания называются замкнутыми. Их операционные характеристики определятся из соотношений:

что система массового обслуживания имеет s каналов обслуживания. Интенсивность каждого канала обслуживания одинакова и равна , так что суммарная интенсивность системы массового обслуживания равна s 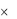. Следовательно, для устойчивого функционирования системы необходимо, чтобы s 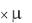было больше интенсивности входящего потока . Операционные характеристики такой системы определятся из соотношений:

массового обслуживания. Возможны различные комбинации уже рассмотренных случаев. Например, (М/ М / S) : (FCFS / m / ∞) или

115

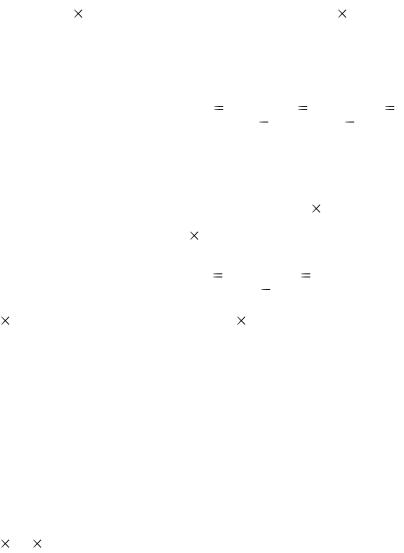
(М / М / S ) : (F C F S / ∞ / m ) и др.

В заключение приведём пример использования стоимостных показателей при анализе систем МО.

Пусть имеется система МО типа (М / М / 1) с λ = 2 и μ = 3. Известно, что издержки ожидания в очереди равны 60 руб. за час, а издержки функционирования равны 42 руб. за час. Кроме того, имеется аналогичная система МО с большей интенсивностью обслуживания (μ = 4), но и большими издержками обслуживания (54 руб. за час). Необходимо выбрать из них более эффективную, предполагая, что общие издержки систем состоят из издержек обслуживания и ожидания исходя из 8-часового рабочего дня.

Подсчитаем издержки функционирования каждой системы. В первой

ожидания одного требования.

В день в среднем поступает 2 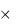8 = 16 требований, следовательно,

второй канал обслуживания с теми же характеристиками, что в первом случае. Будет ли это выгодно, по сравнению со вторым случаем?

116

ожидания 0,0415 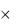16 = 0,0664 (часа). Тогда издержки ожидания равны

600,664 = 39,84 (руб.), а общие издержки: 672 + 39,84 = 711, 84 (руб.).

Сравнивая с 672 руб., видим, что второй случай более выгоден.

Глава 9. Корреляционно-регрессионный анализ взаимосвязей

Значения социально-экономических показателей формируются под влиянием различных факторов, главных и второстепенных, взаимосвязанных между собой и действующих нередко в разных направлениях. Поэтому, кроме локального изучения таких показателей (их уровней, характера изменчивости, распределения и т.д.), важной задачей является изучение связей между различными показателями.

Методами изучения взаимосвязей между показателями и явлениями в статистике являются корреляционный и регрессионный анализы.

9.1 Парная линейная корреляция

Корреляционным анализом называется совокупность приёмов, с помощью которых исследуются и обобщаются взаимосвязи корреляционно связанных величин. В отличие от естественных наук, в социальноэкономическом анализе редко встречаются функциональные связи, здесь взаимосвязи проявляются лишь в общем и среднем, при рассмотрении совокупности явлений в целом, а не отдельных её элементов. Как известно, корреляционная связь заключается в изменении вида распределения, а следовательно, среднего значения одной величины при изменении значения другой. Мерой тесноты линейной корреляционной связи служит коэффициент корреляции Пирсона. Для двух случайных величин x и y он определяется из соотношения

где суммирование ведётся по всем возможным значениям случайных величин x и y, а x и y, соответственно, ожидаемые значения величин x и

117

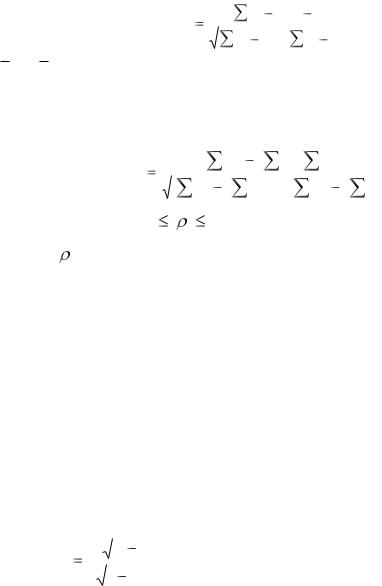
y. Оценкой коэффициента парной (простой) линейной корреляции служит выборочный коэффициент парной корреляции:

где x и y – выборочные средние величины для x и y, а суммирование ведётся по всем элементам выборки. После несложных преобразований можно получить вычислительный вариант этой формулы:

значения одной переменной растёт среднее значение другой, а при 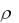< 0 – обратную – с ростом значения одной переменной среднее значение другой убывает. Если ρ = 0, то это означает отсутствие линейной корреляционной связи, а если ρ = 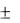1, то это означает наличие между переменными линейной, функциональной связи: прямой в случае (+ 1) и обратной в случае (– 1).

Оценивая значение коэффициента корреляции по выборочным данным, мы должны быть уверены в надёжности такой оценки. Обычно это осуществляется с помощью проверки гипотезы H0: 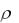= 0 на основе критерия

расчётах вместе с оценками коэффициентов корреляции обычно рассчитываются и уровни значимости для статистик Стьюдента для таких оценок. Если расчётное значение уровня значимости или р-величина для какого-либо выборочного коэффициента корреляции окажется больше фиксированного уровня, например 0,05, то гипотеза Ho не отклоняется, и в этом случае говорят, что коэффициент корреляции не значимо отличен от нуля и линейная корреляционная связь между соответствующими переменными отсутствует. В противном случае говорят, что коэффициент корреляции значимо отличен от нуля, что означает наличие линейной корреляционной связи между соответствующими переменными.

118

Для качественной интерпретации значений коэффициентов парной линейной корреляции (в случае их значимого отличия от нуля) используют шкалу Чеддока:

9.2 Задача анализа матрицы парных коэффициентов корреляции

Корреляционный и регрессионный анализы настолько тесно связаны, что, как правило, редко рассматриваются отдельно друг от друга. Если в корреляционном анализе выявляется наличие и теснота связи, то в регрессионном – конкретный вид такой связи. Одно из различий этих двух видов анализа заключается в том, что в корреляционном анализе переменные равноправны, а в регрессионном анализе они делятся на зависимые и независимые. Такое деление в последнем случае хотя и обязательно, но довольно условно. Осуществляется это исходя из профессионально-логических соображений, и его результат зачастую зависит от цели исследования. Эта терминология не совсем удачно отражает суть дела, и означает лишь то, что в регрессионном анализе значение зависимой переменной восстанавливается по известным значениям независимых переменных. На самом же деле независимые переменные зачастую зависят, в том числе и друг от друга.

Идеальным условием реализации регрессионного анализа является независимость независимых переменных между собой. Ясно, что это практически не выполняется, но совсем уж нежелательно, чтобы между независимыми переменными наблюдалась тесная корреляционная взаимосвязь. В этом случае говорят о коллинеарности переменных. Считается, что две случайные переменные коллинеарны, если коэффициент корреляции между ними не менее 0,8. Если таких переменных несколько, то говорят о мультиколлинеарности. Как уже отмечалось, мультиколлинеарность – нежелательное явление в

119

регрессионном анализе, и её выявление является одной из задач анализа матрицы парных коэффициентов корреляции.

Матрица парных коэффициентов корреляции получается, если для набора переменных y, x1, x2, ..., xm рассчитать парные коэффициенты корреляции и разместить их в виде матрицы. В дальнейшем переменную y будем называть зависимой, а остальные – независимыми. И хотя для корреляционного анализа они равноправны, в целях дальнейшего использования мы их будем различать. Поскольку rxy = ryx, корреляционная матрица симметрична относительно своей главной диагонали, на которой проставлены единицы, поэтому обычно анализируют одну из частей корреляционной матрицы (верхнюю или нижнюю относительно главной диагонали). Пусть корреляционная матрица R имеет вид:

Договоримся анализировать верхнюю часть матрицы. Тогда первая строка матрицы содержит коэффициенты корреляции между зависимой переменной y и независимыми переменными х1, х2, …, xm. Анализируют эти коэффициенты с целью выявления значимых и незначимых независимых переменных. Значимость переменной здесь понимается с точки зрения влияния её на зависимую переменную. Если проверка гипотезы Н0 : 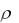= 0 покажет, что коэффициент корреляции незначимо отличен от нуля, то это означает, что соответствующая независимая переменная не значимо влияет на зависимую переменную, т.е. незначима и в уравнение регрессии её включать не следует. Отметим, что подобные выводы правомерны лишь на начальном этапе анализа информации, на самом деле взаимосвязи здесь более сложные, о чём речь впереди.

Второй этап анализа матрицы парных коэффициентов корреляции – выявление мультиколлинеарности среди независимых переменных. Для этого просматривается оставшаяся часть матрицы R (кроме первой строки) и выделяют коэффициенты, по величине 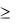0,8. Они и укажут на

120