5576

Если доход в момент времени t обозначить как I(t), то функция потребления отдельных видов товаров может быть записана

матрицу k = {kij} n x n. Допустим, что между выпуском продукции и величиной необходимого для этого капитала существует пропорциональная зависимость. Если прирост производства продукции обозначить как

Из уравнений (2.25) – (2.28) можно вывести основное уравнение динамической межотраслевой модели:

Если обозначить A = A + hV и учесть, что в модели предполагается равновесный рост производства с постоянным темпом прироста q , т.е.

> 0 и в каждой строке матрицы К есть хотя бы один положительный элемент,

21

Следовательно, обладающая экономическим смыслом траектория равновесного роста (траектория Фон Неймана – магистраль) представляет собой вектор { X* :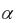 0}, а темп прироста q* в этой модели определяется как величина, обратная

*. Так определяется направление максимального темпа прироста выпусков.

Глава 3. Моделирование производственных процессов

Производственные процессы создают добавленную стоимость и новый экономический продукт, который участвует в последующих процессах обмена и потребления. Производственные процессы протекают в системах, ориентированных как на производство товаров, так и на обслуживание (производство услуг).

Все виды экономического продукта любой производственной системы называются товаром. Производственный процесс – это процесс создания добавленной стоимости путём целенаправленного преобразования одного набора товаров в другой набор товаров. Экономическая система, в которой организован и протекает производственный процесс, называется производством.

Потребляемые в производственном процессе товары называются факторами производства или ресурсами. Полученные в результате производственного процесса товары называются продуктами производства. Производственный процесс может быть однозначно описан количеством потребляемых ресурсов и количеством произведённых продуктов за фиксированный период времени. Будем считать, что между количеством используемых ресурсов и количеством полученных продуктов существует детерминированная связь. При изменении потребляемых ресурсов изменяется выход продукции. С этой точки зрения любая производственная система со сложной внутренней структурой рассматривается как чёрный ящик. Метод чёрного ящика предполагает существование причинно-следственных связей между входами и выходами любой производственной системы неизвестной внутренней структуры. Таким образом, любую производственную систему можно полностью и однозначно определить входными и выходными состояниями. Говорят, что происходит взаимно однозначное отображение

22

входных состояний на выходные состояния системы с помощью ненаблюдаемых внутренних процессов. Модель чёрного ящика описывает существующую систему, но не может быть использована для выработки решений о реформировании структуры и процессов внутри системы. Такая модель производства широко используется в экономико-математическом методе производственных функций.

3.1 Производственные функции выпуска продукции

Производственная функция алгебраически связывает входы и выходы производственной системы, т.е. определяет связь между затратами факторов производства и выпуском продукции. Производственные функции для реальных производственных систем оцениваются с помощью статистических методов обработки эмпирических данных.

Производственная функция описывает наиболее эффективные производственные процессы. При этом менее эффективные производственные процессы исключаются из рассмотрения.

Производственные функции могут быть определены для производственных систем различных масштабов – от производственного участка до мировой экономики. Каждая производственная система характеризуется собственной производственной функцией.

Производственные функции используются для анализа свойств системы и управления производством. С помощью производственных функций можно оценить эффективность функционирования системы и использования отдельных производственных факторов, определить возможности и последствия замещения одних факторов производства другими, изучить воздействие управленческих и технологических инноваций на производственные процессы.

Связь между количеством произведённого продукта и количествами затраченных факторов в виде производственной функции обычно математически представляется с помощью непрерывно дифференцируемой функции, имеющей первые и вторые производные.

Часто рассматриваются факторы производства в виде набора двух агрегированных товаров – капитала K и труда L. Это упрощает процесс моделирования, улучшает точность оценки параметров модели по имеющимся

23

эмпирическим данным на основе эконометрических методов и даёт возможность графического представления набора товаров в виде точки на плоскости.

При анализе производства с помощью набора затрат факторов в форме капитал – труд производственная функция системы связывает количество полученного продукта Y с затратами факторов труда L и капитала K за

Рассмотрим основные свойства производственных функций для случая двух факторов производства. Производственная функция называется неоклассической, если она обладает следующими четырьмя свойствами.

Первое свойство неоклассической функции показывает, что при отсутствии затрат одного из факторов производства получаем нулевой продукт. В нашем случае это означает, что невозможно произвести никакой продукт без затрат труда или капитала.

Второе свойство неоклассической функции показывает, что при увеличении затрачиваемых факторов производства до определённого уровня количество производимого продукта увеличивается.

Третье свойство неоклассической функции связано с её вогнутостью. Свойство вогнутости производственной функции математически выражает закон убывания предельной эффективности производства продукта при увеличении затрат факторов, т.е. при увеличении затрат труда и капитала эффективность их преобразования в продукт уменьшается.

Четвёртое свойство неоклассической функции требует, чтобы функция обладала свойством линейной однородности, т.е. чтобы при одновременном изменении количества всех затрат в 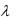раз количество произведённого продукта в системе тоже изменилось в 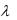раз. Данное свойство является следствием линейности технологических процессов.

Свойство линейной однородности неоклассической производственной функции двух переменных позволяет преобразовать её в функцию одной

24

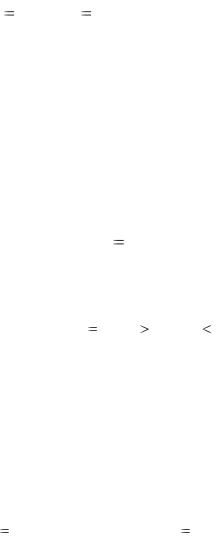
переменной и уменьшить число независимых аргументов до одной переменной. Для этого запишем производственную функцию в виде (3.1) и преобразуем, используя её линейную однородность

Разделив обе части этого уравнения на L , получим

Y / L 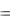f (1, K / L).

Назовём фондовооружённостью k отношение затрат капитала к затратам труда, а средней производительностью труда отношение произведённого продукта к затратам труда. Тогда полученное уравнение для модифицированной производственной функции, связывающей среднюю производительность труда y и фондовооружённость k , примет вид

производственной функции f справедливы следующие соотношения: f (0) 0, f ´ 0, f ´´ 0.

Рассмотрим основные показатели эффективности производства на примере неоклассической производственной функции. Назовём средним продуктом соответствующего фактора производства отношение количества произведённого продукта к количеству затраченного фактора за фиксированный момент времени. Так, средняя фондоотдача AYK и средняя производительность труда AYL определятся как

AYK Y / K 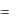f (K, L) / K, AYL Y / L 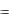f (K, L) / L.

Средняя фондоотдача – это средний продукт капитала, равный среднему количеству произведённого продукта единицей капитала, а средняя производительность труда – это средний продукт труда, равный среднему количеству произведённого продукта единицей труда.

Влияние малого изменения величины потребляемого фактора определяется через понятие предельного продукта фактора. Чем меньше предельный продукт фактора, тем больше должно быть увеличение затрат фактора, которое вызывает увеличение производства на одну единицу продукта.

Увеличение затрат фактора приводит к уменьшению среднего продукта фактора. Это происходит в результате вогнутости производственной функции.

Предельный продукт фактора – это дополнительный продукт, произведённый системой при затратах дополнительной единицей

25

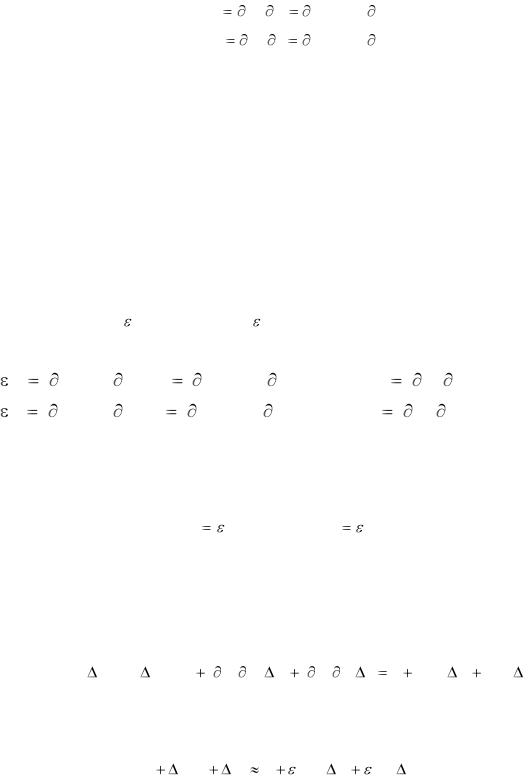
соответствующего фактора. Математически предельный продукт фактора

С увеличением затрат фактора предельный продукт монотонно уменьшается.

Из вогнутости производственной функции следует, что средний продукт фактора всегда больше предельного продукта фактора.

Введём понятие эластичности продукта по фактору. Коэффициент эластичности или просто эластичность продукта по фактору показывает изменение производимого продукта, выраженное в процентах, при изменении фактора на один процент.

В случае двух факторов вводятся понятия коэффициентов эластичности выпуска по фондам K и по труду L . Определяются они соответственно из выражений

Из этих соотношений следует, что предельный продукт фактора равен среднему продукту, умноженному на соответствующий коэффициент эластичности;

позволяет вычислить изменение выпуска производимого продукта при одновременном изменении объёмов затрачиваемых факторов.

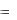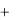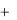Раскладывая производственную функцию Y f (K, L) в ряд Тейлора имеем f (K K, L L) 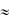f ( f / K) K ( f / L) L y MYK K MYL L,

причём правая часть равенства высчитывается в точке (L, K). Воспользовавшись соотношениями (8.4) получим

26

3.2 Производственная функция Кобба-Дугласа

Будем считать, что для рассматриваемой экономической системы определён частный случай производственной функции – производственная функция Кобба-Дугласа, которая имеет вид

где С – масштабный множитель.

Легко показать, что эта функция удовлетворяет всем свойствам неоклассической производственной функции, 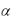– коэффициент эластичности выпуска по капиталу (0 < 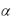< 1), а (1– ) – по труду.

Рассмотрим основные показатели эффективности производства производственной функции Кобба-Дугласа.

Средняя фондоотдача и средняя производительность труда определятся

Мyk = Ayk, Мyl = (1– ) AyL.

С учётом 0 < 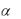< 1 видим, что (как и в общем случае) предельный продукт фактора всегда меньше среднего (закон убывающей эффективности факторов).

Эластичность выпуска по капиталу и труду определяется из соотношений

Пример 3.1. Пусть производственная система характеризуется производственной функцией Кобба-Дугласа. За период времени системой было произведено 100 единиц продукции при затратах 20 единиц труда и 40 единиц капитала. Известно, что 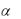= 0,75.

1.Записать производственную функцию Кобба-Дугласа.

2.Сколько единиц продукта будет произведено системой при затратах 25 единиц труда и 50 единиц капитала?

27

3.Определить для данной производственной системы средние продукты труда и капитала

4.Определить предельные продукты труда и капитала.

5.Проверить вычислениями равенства (3.10).

Решение 1. Подставим в (3.5) исходные данные: 100 = С*400.75*200.25. После

вычислений получим: 100 = С*33,64 или С = 100/33,64 = 2,973. Окончательно имеем: Y = 2,973 K0,75L0,25.

2.Подставим в полученное выражение для производственной функции новые данные: Y = 2,973*500,75*250,25 = 125. Таким образом, системой при новых данных будет произведено 125 единиц продукта.

3.Подсчитаем средние продукты факторов, используя формулы (3.6). AyK = 100/40 = 2,5. И AyK = 2,973* (20/40)0,25 = 2,5;

0,25*2,973*20,75 = 1,25 или МyL =(1– ) AyL = 0,25*5 = 1,25.

Сравнивая средние и предельные продукты факторов, видим, что действительно, предельные продукты меньше средних, подтверждая тем самым закон убывающей эффективности факторов.

Средний продукт капитала, равный 2,5, означает, что в рассматриваемой экономической системе на единицу основных фондов приходится в среднем 2,5 единиц выпускаемого продукта, а предельный продукт капитала, равный 1,875, означает, что в экономической системе на единицу прироста основных фондов приходится в среднем 1,875 единиц прироста выпуска продукта. Аналогично и по продукту труда.

5. Пусть левая часть выражения (3.10) – это выпуск, подсчитанный в п. 7.2 при K = 10, а L = 5. Подсчитаем правую часть выражения (3.10):

Y + 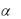(Y/K) K + (1– ) (Y/L) L = 100 + 0,75*(100/40)*10 + 0,25* (100/20)*5 =

125. Как видим, равенство выполнено точно.

28

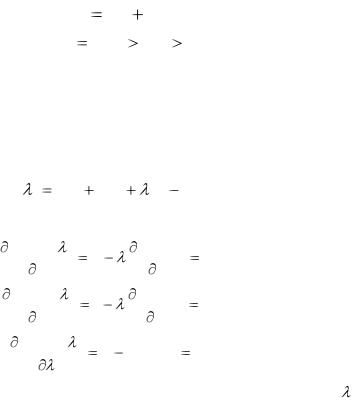
3.3 Функция затрат

Анализ затрат в производственных системах играет важную роль в принятии управленческих решений. При выборе оптимального варианта производства продукции нужно сравнивать возможные альтернативы и выбирать решение, которое обеспечивает минимальные затраты при заданном выпуске производимой продукции или максимальный выпуск продукции при заданном уровне используемых ресурсов.

Известно, что эти две задачи: максимизации выпуска при фиксированной полной стоимости ресурсов и минимизации полной стоимости ресурсов при фиксированном уровне выпуска – имеют одинаковое решение и называются двойственными. Рассмотрим первую задачу, введя понятие функции затрат производственной системы.

Функция затрат равна минимальной полной стоимости набора ресурсов, необходимого для выпуска заданного количества продукта. Пусть производственная система задана производственной функцией Y 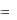f (K, L) . Кроме того, известны объём платёжных средств производителя С и цены единицы труда w и капитала r. Будем предполагать, что цены единицы труда w и капитала r определены рынком ресурсов и являются постоянными величинами. Для нахождения функции затрат необходимо решить задачу оптимизации:

minC rK wL ;

f (K, L) Y, K 0, L 0,

где r, w и Y – положительные постоянные, а K и L необходимо определить.

Задача может быть решена методом множителей Лагранжа, для чего построим функцию Лагранжа и приравняем её частные производные по K, L и

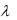к нулю:

29

оптимальный набор факторов производства наименьшей полной стоимостью, который обеспечивает выпуск заданного количества продукта Y .

Вычислим функцию затрат для частного случая производственной системы, которая описывается производственной функцией Кобба-Дугласа.

Пусть задано бюджетное ограничение, которое определяется полной стоимостью набора ресурсов С и ценами единицы труда w и единицы капитала r

C rK wL .

Это и есть затраты экономической системы, необходимые для производства фиксированного уровня получаемого продукта.

Определим величину x как отношение стоимости капитала к полной стоимости капитала и труда:

Тогда, при заданном x имеем соотношения для затрат капитала и труда:

постоянной, а количество получаемого продукта изменяется и может быть определено по формуле

Найдём значение величины x , при котором выпуск продукции достигает максимума. В этой точке производная производственной функции обращается в нуль.

30