
5576
.pdf
коллинеарные переменные. Обычно в уравнение рагрессии не включают те из них, которые слабее связаны с зависимой переменной.
9.3 Уравнение линейной регрессии
Если в регрессионном анализе рассматривается пара переменных – одна зависимая и одна независимая, то говорят о парной (простой) регрессии. Если независимых переменных более одной, то говорят о множественной регрессии. Парная регрессия удобна тем, что её можно отразить визуально на чертеже, и мы будем обращаться к ней именно с этой целью, хотя ясно, что реальные зависимости требуют рассмотрения множественной регрессии. В дальнейшем будем рассматривать только линейную регрессию, поскольку считается, что большую часть зависимостей при изучении социально-экономических явлений можно с определённой степенью точности описать линейными соотношениями, а если это не так, то с помощью определённых преобразований переменных свести к линейным.
Итак, уравнение множественной линейной регрессии в общем виде может быть записано так:
y = a + b1x1 + b2x2 + …+ bmxm + ,
где а – свободный член уравнения регрессии;
bk – коэффициенты регрессии при переменных xk;
 – отклонения фактических значений зависимой переменной от
– отклонения фактических значений зависимой переменной от
расчётных. |
|
|
|
Если расчётные значения обозначить через |
у , то |
||
|
|
|
ˆ |
у = a + b x |
+ …+ b x |
, |
|
ˆ |
1 1 |
m m |
|
т.е. это те значения зависимых переменных, которые лежат на гиперплоскости, определяемой этим уравнением (в двумерном случае – на
линии регрессии). Тогда имеем: y = |
у + |
или |
= y – |
у . Отметим, что а |
||
|
|
|
ˆ |
|
|
ˆ |
|
|
|
|
|
||
и bk ( k = 1, m ) не параметры |
уравнения |
регрессии, а их оценки, |
||||
получаемые обычно на основе метода наменьших квадратов (МНК). Суть МНК состоит в определении оценок параметров уравнения регрессии
121
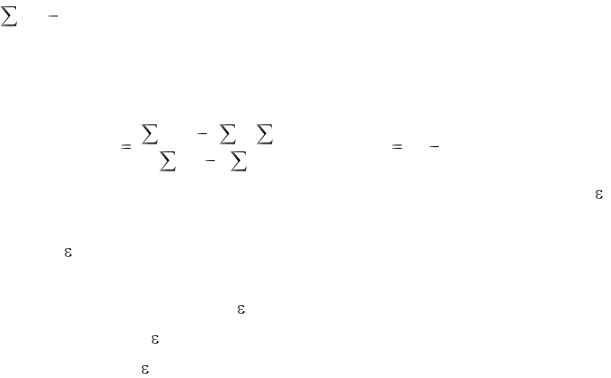
(свободного члена и коэффициентов регрессии) из условия минимизации
(yi yˆ i )2 , т.е. чтобы в среднем расчётные значения уˆ i как можно меньше отличались бы от эмпирических yi. Реализация этого метода в случае парной регрессии: y = a + bx + 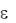 даёт следующие вычислительные формулы для оценок параметров этого уравнения:
даёт следующие вычислительные формулы для оценок параметров этого уравнения:
|
|
xi yi |
( xi |
yi ) / n |
|
|
|
|
|
|
(9.1) |
|
|
b |
, |
a y b x . |
|||||||||
|
x 2 |
( |
x |
)2 / n |
||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
i |
|
|
|
|
|
|
|
|
Для реализации МНК необходимо, чтобы относительно остатков |
||||||||||||
выполнялись следующие предпосылки: |
|
|
|
|
|
|
|
|||||
1) |
является случайной величиной, имеющей нормальный закон |
|||||||||||
распределения; |
|
|
|
|
|
|
|
|
|
|
|
|
2) |
ожидаемое значение |
равно нулю; |
|
|
|
|
|
|
||||
3) |
дисперсия постоянна; |
|
|
|
|
|
|
|
|
|||
4) значения не зависят друг от друга.
Оценки МНК в случае выполнения перечисленных предпосылок являются несмещёнными, состоятельными и эффективными. Если 3) и 4) нарушены, то первые два свойства сохраняются, но оценки становятся менее эффективными.
Свободный член уравнения регрессии (а) обычно не интерпретируется, а коэффициенты уравнения регрессии (bk) показывают, насколько изменится значение зависимой переменной, если значение соответствующей независимой переменной (xk) изменится на единицу при фиксированных значениях других. Но это так, если выполняется основная предпосылка регрессионного анализа – независимость между собой независимых переменных. В случае же мультиколлинеарности смысл коэффициентов уравнения регрессии вообще искажается. К этому мы ещё вернёмся, а сейчас отметим, что коэффициенты уравнения регрессии, как и всякие абсолютные показатели, не могут быть использованы в сравнительном анализе, если единицы измерения соответствующих переменных различны. Например, если y – расходы семьи на питание, х1 – размер семьи, а х2 – общий доход семьи и мы определяем зависимость типа y = a + b1x1 + b2x2 + 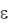 и b2 > b1, то это не значит, что y2 сильнее влияет
и b2 > b1, то это не значит, что y2 сильнее влияет
122

на y, чем х1, т.к. b2 – это изменение расходов семьи при изменении доходов на 1 руб., а b1 – изменение расходов при изменении размера семьи на 1 человека.
Сопоставимость коэффициентов уравнения регрессии достигается при рассмотрении стандартизованного уравнения регрессии:
|
|
y0 = 1x10 + |
2x20 + … + |
|
mxm0 + , |
|
||||||
где y0 |
и |
x0k – стандартизованные значения переменных |
y и xk: |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
0 y y |
, x |
0 |
x |
xk |
, |
|
|||
|
|
|
Sy |
k |
Sx |
|
||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
k |
|
|
|
где Sy |
и |
Sxk – стандартные отклонения |
y |
и xk, а k – |
-коэффициенты |
|||||||
уравнения регрессии, которые показывают, на какую часть своего
стандартного отклонения |
Sy |
изменится зависимая переменная y, если |
||||
независимая переменная |
xk |
изменится на величину своего стандартного |
||||
отклонения Sxk. |
|
|
|
|
|
|
|
|
βk |
|
Sx |
|
|
|
|
bk |
k |
|
||
|
|
|
|
|
||
Sy
-коэффициенты уравнения регрессии создают реальное представление о воздействии независимых переменных на моделируемый показатель. Если величина -коэффициента превышает значение соответствующего парного коэффициента корреляции, то влияние зависимой переменной на y следует признать значимым. Кроме того, совпадение знаков при парных коэффициентах корреляции и
-коэффициентах логически подтверждает правильность включения выбранных показателей в модель. Для получения стандартизованного уравнения регрессии рекомендуется использовать МНК к стандартизованным переменным, а не пересчитывать коэффициенты по указанной формуле.
Наравне с -коэффициентами для анализа воздействия показателей, включённых в уравнение регрессии, на моделируемый признак, используются коэффициенты эластичности:
Э |
|
b |
|
|
xk |
, |
||
k |
k |
|
|
|
||||
|
y |
|||||||
|
|
|
|
|||||
|
|
|
|
|
|
|
||
123
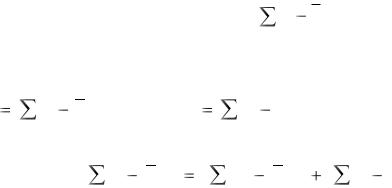
которые показывают, на сколько процентов изменится зависимая переменная, если соответствующая независимая переменная изменится на один процент.
9.4 Оценка точности уравнения регрессии
Как уже отмечалось, оценки параметров уравнения регрессии вычисляются по выборочным данным и лишь приближённо равны этим параметрам. В связи с этим появляется необходимость оценить точность как уравнения регрессии в целом, так и его параметров в отдельности. При решении первой задачи используют процедуру дисперсионного анализа, основанную на разложении общей суммы квадратов отклонений зависимой переменной: SST 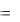 (y y)2 на две составляющие, источниками которых являются отклонения за счёт регрессионной
(y y)2 на две составляющие, источниками которых являются отклонения за счёт регрессионной
зависимости |
(SSR) |
и за счёт |
случайных |
ошибок (SSE), причём |
|||
SSR |
(y |
y)2 , |
а SSE |
(y |
y) 2 . |
Из |
теории статистики |
|
|
|
|
|
ˆ |
|
|
известно, что SST = SSR + SSE или |
|
|
|
||||
|
|
(y |
y)2 |
(y |
y)2 |
(y |
y) 2 . |
|
|
|
|
|
|
|
ˆ |
|
Аналогичное разложение имеет место и для числа степеней свободы |
||||||
соответствующих сумм: |
|
|
|
|
|||
|
|
|
dfT |
= dfR + dfE , |
|
|
|
где |
dfT = n – 1 – общее число степеней свободы; |
|
|||||
dfR = m – число степеней свободы, соответствующее регрессии (m – число независимых переменных в уравнении регрессии);
dfE = n – m – 1 – число степеней свободы, соответствующее ошибкам. Разделив соответствующие суммы квадратов на степени свободы,
получим средние квадраты или дисперсии, которые сравниваются по критерию Фишера для проверки гипотезы о равенстве нулю одновременно всех коэффициентов регрессии против альтернативной: не все коэффициенты регрессии равны нулю. Если нулевая гипотеза отклоняется, то это означает, что уравнение регрессии значимо, в противном случае оно ничего не отражает и не может быть использовано в анализе.
Итак, процедура дисперсионного анализа регрессии состоит в
124

следующем:
рассчитываются суммы квадратов SSR и SSE;
определяются средние квадраты или дисперсии, соответствующие регрессии и ошибкам: MSR = SSR / m и MSE = SSE / n – m – 1;
сравниваются полученные дисперсии на основе критерия Фишера,
причём MSR MSE, следовательно F |
MSR |
; если F |
/2,m,n-m-1 > F, |
|
MSE |
||||
|
|
|
то уравнение регрессии значимо (не все коэффициенты уравнения регрессии равны нулю), в противном случае – не значимо.
Дисперсионный анализ регрессии удобно проводить в таблице вида: Таблица 9.1 – Таблица дисперсионного анализа регрессии
Источник |
Сумма |
Степени |
Средние |
F-отношение |
|||
|
квадратов |
свободы |
квадраты |
|
|
|
|
|
|
|
|
|
|
|
|
Модель |
SSR |
m |
MSR |
F= |
MSR |
|
|
ошибки |
SSE |
n – m – 1 |
MSE |
MSE |
|||
|
|||||||
|
|
|
|
|
|
|
|
Общая |
SST |
n – 1 |
|
|
|
|
|
Вернёмся к MSE. Это тоже характеристика точности уравнения регрессии. Этот показатель особого самостоятельного значения не имеет, но участвует в вычислении других показателях точности. Например, корень квадратный из MSE называется стандартной ошибкой оценки по регрессии (Sy,x) и показывает, какую ошибку в среднем получим, если значение зависимой переменной оценивать по уравнению регрессии:
|
|
|
|
(y |
y)2 |
|
|
|
|
|
|
||||
SY, X |
MSE |
|
|
|
ˆ |
. |
|
|
|
n |
m 1 |
||||
|
|
|
|
|
|
||
Кроме того, этот показатель в неявном виде участвует в определении коэффициента множественной детерминации (R2):
R 2 1 SSE SST
или после преобразований:
R 2 |
|
SST SSE |
|
SSR |
. |
|
|
|
|
|
|||
|
|
SST |
|
SST |
||
Отсюда следует, что |
коэффициент |
множественной детерминации |
||||
125

отражает долю вариации изучаемого (результирующего) показателя, обусловленную вариацией за счёт регрессионной зависимости. Коэффициент множественной детерминации иногда выражают в процентах, поэтому, например, если R2 = 75%, то это означает, что изменение зависимой переменной на 75% объясняется изменением включённых в уравнение регрессии независимых переменных, а остальные 25% – это изменения за счёт неучтённых факторов и случайных отклонений (ошибок).
Корень квадратный из коэффициента множественной детерминации называется коэффициентом множественной корреляции:
|
|
|
|
|
R 1 |
SSE |
, |
||
|
||||
SST |
||||
|
|
|
||
который показывает тесноту линейной корреляционной связи между зависимой переменной и всеми независимыми переменными.
Ясно что, R2 и R изменяются от нуля до единицы и равны единице, если SSE = 0, т.е. связь линейная функциональная и равны нулю, если SST = SSE, т.е. связь отсутствует.
Значимость коэффициента множественной детерминации определяется на основе критерия Фишера:
F |
R 2 |
(n |
m 1) |
(1 |
|
R 2 ) m |
|
|
|
с m числом степеней свободы числителя и |
n – m – 1 – знаменателя. |
||||||
В социально-экономических исследованиях встречается преобразованная |
|||||||
формула определения R2 , имеющая вид: |
|
|
|
||||
R 2 |
1 |
MSE (n |
m 1) |
||||
|
|
|
|
|
|
||
MST (n |
1) |
|
|
||||
|
|
|
|
||||
или в других обозначениях: |
|
|
|
|
|
|
|
R 2 |
1 |
Sy,x |
2 (n m 1) |
, |
|||
|
|
||||||
|
|
Sy |
2 (n |
1) |
|
|
|
где Sy,x2 – выборочная остаточная дисперсия независимого показателя; Sy2 – его общая выборочная дисперсия.
Как уже отмечалось, 
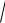 S2 y,x – стандартная ошибка оценки по регрессии.
S2 y,x – стандартная ошибка оценки по регрессии.
126

Из определения коэффициента множественной детерминации следует, что он будет увеличиваться при добавлении в уравнение регрессии независимых переменных, как бы слабо ни были они связаны с независимой переменной. Следуя этой логике, для увеличения точности отражения изучаемой зависимости в уравнение регрессии может быть включено неоправдано много независимых переменных. Точность модели при этом увеличится незначимо, а размерность модели возрастёт так, что её анализ будет затруднён. Кроме того, качество оценок при этом ухудшается. Для исключения такого недостатка рассматривают исправленный (на число степеней свободы) коэффициент множественной детерминации:
|
|
n |
1 |
|
|
|
R 2 |
1 (1 R 2 ) |
. |
||||
|
|
|
||||
n |
m 1 |
|||||
|
|
|
||||
Этот коэффициент позволяет избежать переоценки независимой переменной при включении её в уравнение регрессии. Если добавление
переменной приводит к увеличению R 2 , то включение её в уравнение регрессии оправдано, в противном случае – нет. Исправленный коэффициент детерминации всегда меньше неисправленного и является несмещённой оценкой для коэффициента множественной детерминации, в то время как неисправленный – завышенный, смещённой оценкой.
Продолжим анализ точности уравнения регрессии. Как уже отмечалось, при проверке значимости уравнения регрессии проверяется гипотеза о том, что все коэффициенты уравнения регрессии равны нулю, против альтернативной – не все коэффициенты регрессии равны нулю. В последнем случае, т.е. если нулевая гипотеза отклонена, встаёт вопрос: какие из коэффициентов равны нулю, а какие значимо отличны от нуля?
9.5 Проверка значимости коэффициентов уравнения регрессии
Осуществляется она на основе статистик Стьюдента, построенных для этих коэффициентов.
Для свободного члена ta = a / Sa,
где Sa – стандартная ошибка свободного члена уравнения регрессии:
127

Sa  S Y,X /
S Y,X / 
 n .
n .
Для коэффициентов регрессии t – статистика равна: tbk = bk / Sbk ,
где Sbk – стандартная ошибка коэффициента регрессии:
|
|
|
|
2 |
|
|
|
|
|
2 |
|
S Y,X |
1 |
, |
|||
|
Sbk |
|
|
|
|
|
|
|
|
2 |
n 1 |
2 |
|||||
|
|
S |
R k |
|
||||
|
|
|
xk |
|
|
|||
где S2xk |
– выборочная дисперсия переменной xk; |
|||||||
Rk2 |
– коэффициент множественной детерминации, характеризующий |
|||||||
зависимость переменной xk от всех остальных.
Вычисленные статистики Стьюдента сравнивают с критическими
значениями |
t |
/2 , найденными по таблице t – распределения с |
= n – 1 |
степенями свободы. |
|
||
Если, |
например, tbk > t /2 , то это означает, что коэффициент при |
||
переменной |
xk |
в уравнении регрессии значимо отличен от нуля и влияние |
|
переменной xk на моделируемый показатель можно признать значимым. Отметим, что равенство нулю свободного члена уравнения регрессии
означает, что начало координат рассматриваемого признакового пространства удовлетворяет уравнению регрессии, т.е. гиперплоскость уравнения регрессии проходит через начало координат. Эта информация может быть полезна при качественном анализе уравнения регрессии.
Обратимся к формуле стандартной ошибки коэффициента уравнения регрессии. Множитель 1 / (1 – Rk2) введён в эту формулу, чтобы отразить влияние корреляции между переменными на величину стандартной ошибки. Как уже отмечалось, идеальным условием МНК является независимость объясняющих переменных друг от друга. В этом случае Rj2 = 0 и стандартная ошибка коэффициента регрессии принимает наименьшее значение. В случае мультиколлинеарности переменных, соответствующие Rk2 1 и стандартная ошибка увеличивается. Сам коэффициент регрессии теряет при этом познавательную ценность. В предельном случае (R2 = 1) система нормальных уравнений для оценки коэффициентов уравнения регрессии становится вырожденной и уравнение регрессии не может быть получено.
128
9.6 Автокорреляция отклонений (остатков)
Как уже отмечалось, одной из предпосылок МНК является независимость отклонений 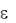 = y – уˆ друг от друга. Если же это условие нарушено, то говорят об автокорреляции остатков. Причин возникновения автокорреляции остатков может быть несколько. Выделим среди них следующие:
= y – уˆ друг от друга. Если же это условие нарушено, то говорят об автокорреляции остатков. Причин возникновения автокорреляции остатков может быть несколько. Выделим среди них следующие:
1)в регрессионную модель не введён значимый факторный признак
иего изменение приводит к закономерному изменению остаточных величин;
2)в регрессионную модель не включено несколько незначимых факторов, но их изменения совпадают по направлению и фазе и суммарное воздействие приводит к закономерному изменению остатков;
3)не верна спецификация уравнения регрессии. При автоматизации вычислительных работ исключим случай ошибок при вычислении оценки коэффициентов регрессии и укажем лишь на одну из возможных причин неправильной спецификации – не верно выбран вид зависимости между анализируемыми переменными;
4)автокорреляция остатков может возникнуть не в результате ошибок, допущенных при построении регрессионной модели, а вследствие особенностей внутренней структуры случайных компонент (например, при описании регрессией динамических рядов).
Следовательно, необходимо при анализе точности уравнения регрессии уметь определять наличие или отсутствие автокорреляции в остатках.
Разработано несколько методов проверки на автокорреляцию остатков. Большинство статистических пакетов прикладных программ используют метод Дарбина – Уотсона. Опишем его. Он основан на гипотезе о существовании автокорреляции между соседними членами ряда остатков. Этот критерий использует статистику
129
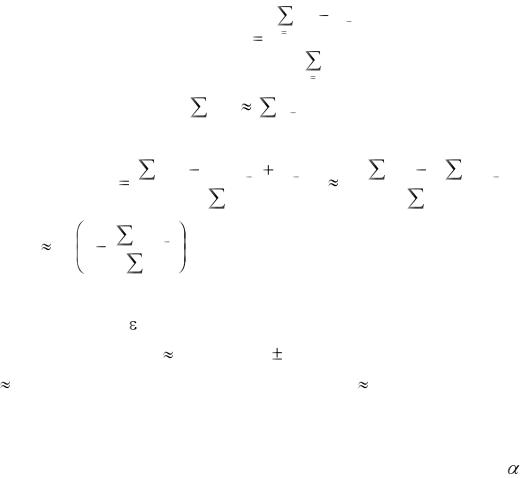
|
n |
|
|
|
|
)2 |
|
|
(ε |
i |
ε |
i 1 |
|
||
|
|
|
|
|
|
||
d |
i 2 |
|
|
|
|
|
. |
|
n |
2 |
|
|
|||
|
|
|
|
|
|||
|
|
|
εi |
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
Предполагая, |
что |
εi |
2 |
|
εi 12 |
(при достаточно больших n это |
||||||||||
так) получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
(εi 2 |
2εi εi 1 |
εi 12 ) |
|
2 εi 2 |
2 εi εi 1 |
, |
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
εi |
|
|
|
εi |
2 |
|
|
или |
d 2 1 |
|
εi |
εi |
1 |
|
. |
|
|
|
|
|
|
|
|
||
|
|
εi |
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Вычитаемая из единицы дробь равна коэффициенту автокорреляции |
||||||||||||||||
для |
переменной i |
и, следовательно, равна нулю, если автокорреляция |
|||||||||||||||
отсутствует (тогда d |
|
|
2), и равна |
1 при полной автокорреляции (тогда |
|||||||||||||
d 0 при положительной автокорреляции и d 4 – при отрицательной). Для d-статистики найдены критические границы (du – верхняя и dl –
нижняя), позволяющие принять или отклонить гипотезу об отсутствии
автокорреляции при фиксированном уровне значимости |
, числе |
независимых переменных m и объёме выборки n. |
|
Область принятия и непринятия гипотезы об отсутствии автокорреляции в остатках графически может быть изображена в таблице 9.2.
Таблица 9.2 – Область принятия гипотезы, области неопределённости и непринятия гипотезы для критерия Дарбина – Уотсона
Область |
Область |
|
|
Область |
|
Область |
|
|
Область |
непринятия |
неопределён- |
|
|
принятия |
|
неопределён- |
|
|
непринятия |
гипотезы |
ности |
|
|
гипотезы |
|
ности |
|
|
гипотезы |
(положительная |
|
|
|
(автокорр. |
|
|
|
(отрицательная |
|
автокорреляция) |
|
|
|
отсутствует) |
|
|
|
автокорреляция) |
|
|
|
|
|
|
|
|
|
|
|
0 |
dl |
du |
|
4-du |
4-dl |
4 |
|||
Если вычисленное значение d-статистики попало в область неопределённости критерия, то это означает, что нет статистических оснований ни отклонить, ни принять гипотезу об отсутствии автокорреляции в остатках. В этом случае при необходимости можно
130
