Себестоимость продукции на действующих заводах С1 = 5, C2 = 4. Себестоимость после реконструкции С1 = 4. Себестоимость на новом заводе С3 = 2. Удельные капитальные затраты заданы: Еk1 = 6, Еk3 = 8. Определить оптимальный вариант прироста мощностей и план перевозок.

Решение. Производственно-транспортные затраты на действующих предприятиях складываются из затрат на производство и доставку единицы продукции Сi + Cij.Для вариантов строительства и реконструкции к этим затратам добавляются удельные капитальные затраты с учётом нормативного коэффициента эффективности: Сi + Cij + Е ∙ Кi.

С учётом вышеизложенного получаем матрицу приведённых затрат:

Далее решается открытая транспортная задача по методу потенциалов. После трёх итераций получаем оптимальное решение. Полученное решение целочисленное. Zmin = 2880. Выбирается вариант строительства, т.к. вариант реконструкции А1 полностью прикрепился к фиктивному потребителю. Оптимальное решение представлено в таблице 4.3.

Таблица 4.3 – Оптимальное решение задачи

Optimal Solution Total Cost = 2880.00

Number of iterations = 3

51

4.5.3 Двухэтапная производственно-транспортная задача

Производимая продукция иногда проходит последовательную обработку на нескольких предприятиях, и в этом случае необходимо комплексное решение проблемы размещения предприятий на всех стадиях. Кроме того, при размещении предприятий необходимо учитывать их зависимость от пунктов снабжения сырьём. В таких случаях приходится рассматривать многоэтапные модели размещения.

Рассмотрим простейший случай, когда система состоит из трёх этапов: сырьё – переработка – потребитель. Пусть имеется р сырьевых районов, n пунктов потребления и m возможных пунктов производства.

i

52

i

Ограничения модели характеризуют:

(4.36) – балансы распределения сырья по каждому сырьевому району; (4.37) – балансы удовлетворения потребителей в сырье в каждом пункте производства; (4.38) – балансы производства и распределения продукции в каждом пункте;

(4.39) – балансы удовлетворения потребностей в готовой продукции каждого потребителя.

В модели (4.36) – (4.39) комплексно решается проблема размещения предприятий с учётом их связей и с пунктами снабжения сырьём, и с пунктами потребления готовой продукции.

полностью перерабатывается, спрос всех потребностей удовлетворяется. Задача решается по методу «фиктивной диагонали». Предприятия по

производству продукции на первом этапе выступают потребителями сырья, на втором – поставщиками готовой продукции. Причём их мощности определяются из решения задачи. Задача решается в таблице 4.4.

Таблица 4.4 – Метод «фиктивной диагонали»

53

Таблица 4.4 состоит из четырёх блоков. В 1-м блоке отражаются связи поставщиков сырья с перерабатывающими предприятиями. Во втором блоке – связи поставщиков сырья с потребителями готовой продукции. Поскольку потребителям необходима готовая продукция, эти связи запрещаются тарифами М → + ∞, что обеспечивает условие оптимальности для соответствующих клеток таблицы на всех этапах решения. Третий блок образуется строками и столбцами, относящимися к обрабатывающим предприятиям. Продукция перевозится потребителю, а не другому обрабатывающему предприятию, поэтому связи предприятий друг с другом блокируются запретительными тарифами М. При любом расположении блоков в таблице такие клетки будут представлять диагональ соответствующего блока. Ставя здесь нулевые тарифы, мы «разрешаем» сюда поставки, они будут означать размер неиспользованной мощности соответствующего предприятия. Поскольку на самом деле поставки, указанные в этой диагонали, не осуществляются, они фиктивные, а сама диагональ называется фиктивной. В четвёртом блоке отражаются связи пунктов производства продукции с пунктами потребления этой продукции.

Далее задача решается по методу потенциалов. При нахождении первоначального плана заполняется 4-й блок, затем «фиктивная» диагональ, затем 1-й блок.

Если в задаче допускаются прямые связи поставщиков сырья с потребителями готовой продукции, запретительные тарифы М в соответствующих клетках третьего блока снимаются и ставятся реальные тарифы Crj.

54

Глава 5. Целевое программирование

5.1 Постановка задачи

Целевое программирование (ЦП) – это относительно новая концепция, развивающая идеи линейного программирования (ЛП) и призванная помочь в разработке управленческих решений в условиях многих целей. Как известно, одним из условий, при которых задача оптимального планирования может быть сформулирована и решена в рамках ЛП, является наличие единого, чётко сформулированного и количественно определённого критерия оптимальности в виде целевой функции. Обычно это минимум затрат или максимум прибыли. Но практика хозяйственной деятельности показывает, что это не единственные, а порой и не самые главные цели, которые приходится ставить и решать, планируя работу на перспективу. В ЛП предусматривается возможность объединения нескольких целей в одну, но в этом случае цели должны измеряться в одних и тех же единицах измерения (например, в рублях). В действительности цели настолько разнообразны, а порой и противоречивы, что свести их в одну не всегда представляется возможным. Это цели и престижа фирмы, и охраны окружающей среды, и поддержания определённого социальнопсихологического климата в коллективе и т.д., которые и в отдельности-то измерить не просто.

Одним из возможных направлений реализации подобного рода задач и явилась разработка в начале 60-х годов прошлого столетия идей целевого программирования.

В условиях многих целей и ограниченности ресурсов не все цели могут быть достигнуты. В ЦП предусматривается такая возможность, и для её реализации вводится новый тип переменных, показывающих степень отклонения достигнутого уровня целей от желаемого. Такие переменные будем называть отклонениями. Не следует смешивать их с балансовыми переменными в ЛП. Балансовые переменные в ЛП показывают, насколько правая часть ограничения отличается от левой, а

55

переменные – отклонения в ЦП отражают степень недоили перевыполнения конкретной цели. Кроме этих особенностей, ЛП и ЦП отличаются конструкцией целевой функции. Если в ЛП непосредственно оптимизируется одна конкретная цель, то в ЦП минимизируются отклонения между желаемыми и достигнутыми уровнями многих целей (в пределах ограничений по ресурсам). Отсюда и роль отклонений. Если в ЛП балансовые переменные являются вспомогательными, то в ЦП отклонения играют решающую роль и формируют целевую функцию.

В условиях многих целей из-за ограниченности ресурсов одни цели могут быть достигнуты за счёт других. А это приводит к необходимости установления определённой иерархии целей так, чтобы цели нижнего приоритета выполнялись бы только при условии реализации целей высшего приоритета. А поскольку возможна ситуация, когда не все цели могут быть достигнуты, то ЦП реализует алгоритм достижения возможного (удовлетворительного) уровня многих целей. Этим оно отличается от ЛП, в котором оптимальное решение рассчитывается для одной цели.

Для установления приоритета целей, отклонения в целевой функции в ЦП взвешиваются при помощи специальных коэффициентов. Каждая цель формируется при помощи целевого ограничения, включающего в себя отклонения от цели. Кроме целевых ограничений, модель задачи ЦП может содержать и обычные, системные ограничения, подобные ограничениям в ЛП. Поскольку отклонения от цели могут быть в обе стороны, то для каждой цели обычно вводят по две отклоняющих переменных, показывающих недо- и перевыполнение цели (обозначаются соответственно через d- и d+ ).

Не следует путать задачи ЦП с многокритериальными задачами или с задачами векторной оптимизации. Это особые разделы математического программирования, которые здесь не рассматриваются.

Рассмотрим реализацию основных идей и методов решения задач ЦП на примере.

Пример 5.1. Предположим, что для производства двух видов продукции фирма расходует два вида ресурсов. Известны нормы расхода

56

каждого вида ресурса на производство единицы каждого вида продукции, объёмы имеющихся ресурсов и прибыль от реализации единицы каждого вида продукции. Используя прошлый опыт и цели, стоящие перед фирмой на ближайшую перспективу, руководство фирмы ставит перед собой следующие цели в порядке их приоритетности:

1.Получить не менее 30 ед. прибыли.

2.По возможности максимально использовать ресурс 1-го вида.

3.Желательно не перерасходовать ресурс 2-го вида.

4.Обеспечить контрактную поставку продукции 2-го вида не менее 7 единиц.

Решение. Для формулировки модели задачи предположим, что прибыль от реализации единицы продукции равна соответственно 7 и 6 единиц, расход 1-го ресурса на выпуск единицы каждого продукта равен 2

и3 единицы соответственно, а объём 1-го ресурса равен 12 единиц. Для 2- го ресурса эти показатели соответственно равны 6, 5 и 30 единиц.

Составим модель задачи ЦП.

Основные неизвестные модели: х1 – объём производства продукции первого вида; х2 – второго вида.

Целевые ограничения:

цели. Если 1-я цель будет недовыполнена, то величина недовыполнения (d1-) будет больше нуля (d1- > 0), тогда величина перевыполнения (d1+) будет равна нулю (d1+ = 0). И наоборот, в случае перевыполнения цели d1+ > 0, а d1- = 0. Если цель будет выполнена в точности, то d1+ = d1- = 0. В любом случае по крайней мере одна из этих переменных будет равна нулю. Поскольку первая по приоритетности цель предусматривает получение не менее 30 ед. прибыли, то в целевой функции будем минимизировать недовыполнение, т.е. для этой цели в целевой функции будет слагаемое P1d1- , где P1 – весовой коэффициент.

Второе целевое ограничение имеет вид: 2x1 + 3x2 + d2- – d2+ = 12, где d2- и d2+ соответственно недо- и перевыполнение 2-й цели. Для максимизации использования 1-го вида ресурса будем минимизировать d2-,

57

следовательно, на этом этапе Z = P1d1- + P2d2-, причём P1 >> P2 (P1 значимо больше P2).

Третье целевое ограничение: 6x1 + 5x2 + d3- – d3+ = 30 и для реализации 3-й цели будем минимизировать d3+, следовательно, на этом этапе формирования целевой функции будем иметь Z = P1d1- + P2d2- + P3d3+.

Для реализации 4-й цели необходимо произвести продукции 2-го вида не менее 7 ед., следовательно, целевое ограничение примет вид:

x2 + d4- – d4+ = 7, а целевая функция – Z = P1d1- + P2d2- + P3d3+ + P4d4 -, где P1 >> P2 >> P3 >> P4 .

Окончательно имеем: минимизировать общее отклонение

Z = P1d1- + P2d2 - + P3d3+ + P4d4-

при условии, что

7x1 + 6x2 + d1 - – d1+ = 30; 2x1 + 3x2 + d2 - – d2+ = 12; 6x1 + 5x2 + d3 - – d3+ = 30;

x2 + d4 - – d4+ = 7; x1, x2, di-, di+ 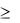0.

Это и есть модель задачи ЦП.

5.2 Модифицированный симплексный метод решения задач целевого программирования

Рассмотрим метод решения задачи ЦП, использующий идеи симплексного метода. Основная особенность задач ЦП заключается в конструкции целевой функции и в переменных, которые показывают отклонения от желаемого уровня достижения целей. Если учесть эти особенности, то для решения таких задач может быть применён обычный симплексный метод. Проиллюстрируем это на рассмотренном ранее примере. Алгоритм в некоторой степени упрощается из-за того, что исходное базисное решение здесь очевидно. Роль базисных переменных для начального плана здесь играют отрицательные отклонения «d i », которые включены в модель с коэффициентами +1. Сложнее со строкой

58

для коэффициентов целевой функции, т.е. с оценочной строкой. Как мы знаем, коэффициентами для отклонений в целевой функции задачи ЦП служат веса, ранжирующие цели по приоритетам. Их численные значения, как правило, не определены. Важно, чтобы коэффициент при отклонении для целевого ограничения с более высоким приоритетом был бы значимо больше коэффициента при отклонении от цели с более низким приоритетом. Поэтому для удобства расчетов оценочная строка разбивается на несколько строк (по числу приоритетов), и вычисления ведутся по каждой строке в отдельности.

по правилу: «от суммы произведений элементов столбца «Св» на элементы соответствующего столбца отнимается элемент верхней строки». Например, для столбца «решение» элемент «Zj – Cj» равен: Р1 *30 + Р2 *12

59

+ 0* 30 + р4 *7 – 0 = 30Р1 + 12Р2 + 7Р4 и коэффициенты при

соответствующих Pi (i = 1,4 ) выписаны в этом столбце в блоке «Zj – Cj» (читать снизу вверх). Для столбца «х1»: Р1 *7 + Р2 *2 + 0 * 6 + Р4 *0 – 0 = 7Р1 + 2Р2 , а это и есть коэффициенты при Р1 и Р2 в блоке «Zj – Cj» и т.д.

Поскольку задача ЦП всегда решается на минимум, то решение будет оптимальным, если все элементы оценочной строки будут не положительны. В нашем случае две оценки (в столбцах «х1» и «х2») положительны, следовательно, план не оптимальный. Для определения переменной, входящей в базис, на первой итерации определяем наибольшую положительную оценку. Определяется она по знаку коэффициента при Р1, т.к. P1 >> P2 >> P3 >> P4. При равных коэффициентах при Р1, «поднимаемся» на строку выше и выбираем наибольший коэффициент там. В случае полного равенства по всем строкам – выбирается любой из них. В нашем случае разрешающим столбцом будет столбец «х1» (т.к. 7 > 6). Разрешающая строка выбирается так же как и в симплексном методе – по наименьшему симплексному отношению 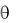(элементы столбца «решение» делим на положительные элементы разрешающего столбца). В таблице 5.1 наименьшее отношение 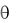находится в первой строке. Итак, на следующей итерации в базис вводится переменная «х1», выводится «d1-». Пересчитываем таблицу как в обычном симплекс-методе (таблица 5.2.)

Таблица 5.2 – Вторая симплексная таблица

60