
5576
.pdf
|
|
1 |
|
1 |
|
f (x ) AC |
|
|
, |
||
|
|
|
|
||
r |
|
|
w |
||
|
|
|
|
||
Функцию затрат в этом случае представим как минимальные средние затраты на единицу выпускаемого продукта, разделив С на f (x ) :
C |
|
|
1 |
1 |
|
A |
|
. |
|||
|
|
|
|
||
f (x ) |
r |
|
w |
||
Следует обратить внимание, что функция затрат определяется ценами единицы труда и капитала, которые определяются состоянием рынка ресурсов производства и являются экзогенными величинами, заданными внешней экономической средой.
В заключение отметим, что в нашем случае мы выписали функцию затрат лишь для частного случая производственной функции – функции КоббаДугласа. Для других производственных функций функции затрат будут другими. Каждой производственной функции соответствует своя функция затрат.
31
Глава 4. Линейное программирование в экономико-математическом моделировании
Существует множество форм деятельности фирм, которые связаны с распределением ресурсов. Эти ресурсы включают труд, сырьё, оборудование и денежные средства. Иногда процесс распределения ресурсов при формировании планов производства называют программированием. Размеры ресурсов, как правило, ограничены, поэтому возникают определённые проблемы. Если фирма выпускает продукцию нескольких видов с использованием одного и того же оборудования и трудовых ресурсов, то её администрация должна решить, какое количество продукции каждого вида производить. Администрация может задаться целью наладить производство таким образом, чтобы максимизировать общий выпуск продукции за определённый период времени, максимизировать время использования оборудования или минимизировать затраты труда. Переменные величины, получающие численные значения в результате решения таких задач, – это количество продукции каждого вида, которое необходимо произвести за данный период времени.
Аналогично, если фирма обладает определённым капиталом для инвестирования ряда проектов, распределение денежных сумм по каждому проекту нужно проводить таким образом, чтобы минимизировать риск или максимизировать темпы роста капитала. Переменные решения в данном случае – это денежные суммы, помещаемые в каждый проект.
В общем случае цель состоит в определении наиболее эффективного распределения ресурсов по соответствующим направлениям, которое оптимизирует некоторый результат функционирования системы. Часто эффективным инструментом в процессе распределения ресурсов являются математические модели. Математическим программированием называется использование математических методов и моделей для решения задач оптимизации социально-экономических программ.
Всякая задача математического программирования включает две группы условий:
а) критерий оптимальности в виде аналитической функции; б) ограничения, определяющие множество допустимых решений.
32
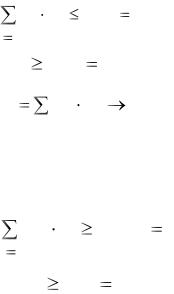
При этом задача нахождения экстремума имеет смысл, если множество допустимых решений не пусто, а целевая функция на этом множестве ограничена.
Множество допустимых решений и критерий оптимальности формируются независимо друг от друга.
Ограничимся в дальнейшем рассмотрением моделей линейного программирования. Задача оптимального планирования сводится к задаче линейного программирования при выполнении следующих условий:
1)в задаче должен быть единый критерий оптимальности;
2)имеется множество допустимых решений, определяемых системой ограничений;
3)переменные в моделях линейного программирования
взаимозаменяемы. Условия задачи должны обеспечить многовариантность
исвободу выбора вариантов;
4)модель задачи должна содержать только линейные уравнения и неравенства.
4.1 Двойственность в линейном программировании
Рассмотрим стандартную и двойственную к ней задачи линейного программирования.
Стандартная задача:
Найти значения переменных х1, х2, ..., хn, удовлетворяющих условиям
n |
|
|
|
|
|
|
|
|
|
|
|
; |
(4.1) |
a |
ij |
x |
j |
|
b |
|
, i |
|
|
1, m |
|||
|
|
|
i |
|
|
|
|
|
|
|
|||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x j |
|
0, j |
|
|
1, |
n ; |
(4.2) |
||||||
Z |
|
C |
j |
x |
j |
max . |
(4.3) |
||||||
|
|
|
|
|
|
|
|
|
|
||||
j
Двойственная задача:
Найти значения переменных у1, у2, ..., уm, удовлетворяющих условиям
n |
|
|
|
|
|
|
|
|
aij |
уi |
C j , |
j 1, n ; |
(4.4) |
||||
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
уi |
0, i |
1, |
m ; |
(4.5) |
||||
33
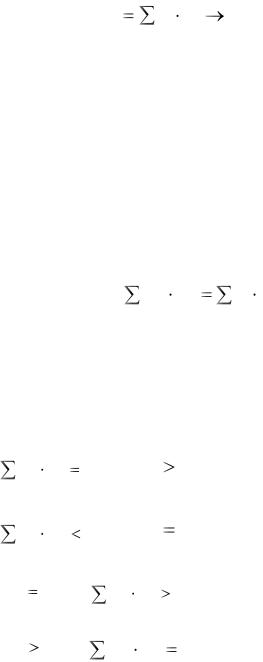
W |
bi yi |
min . |
(4.6) |
|
i |
|
|
Условия (4.1) и (4.5), |
а |
также (4.2) и |
(4.4) называются |
взаимносопряжёнными.
Приведём формулировки основных теорем двойственности, необходимые для дальнейшего рассмотрения.
Теорема 1 (основная). Если задача (4.1) – (4.3) имеет оптимальное решение х*, то и двойственная к ней задача (4.4) – (4.6) также имеет оптимальное решение у*, причём
C |
j |
x* |
b |
y* . |
(4.7) |
|
j |
i |
i |
|
|
j |
|
|
i |
|
|
Теорема 2 (о равновесии). Для каждой пары сопряжённых условий в оптимальном решении прямой и двойственных задач выполняются следующие соотношения: если одно из них выполняется как строгое равенство, то другое – как строгое неравенство и наоборот, т.е.
|
|
* |
|
* |
|
|
|
если |
aij |
bi , то |
yi |
0 ; |
(4.8) |
||
x j |
|||||||
|
j |
|
|
|
|
|
|
если |
aij |
* |
bi , то |
* |
0 ; |
(4.9) |
|
x j |
yi |
||||||
|
j |
|
|
|
|
|
|
если |
* |
0, то |
aij |
yi* |
C j ; |
(4.10) |
|
x j |
|||||||
|
|
|
i |
|
|
|
|
|
* |
|
aij |
* |
C j . |
|
|
если x j |
0, то |
yi |
(4.11) |
||||
i
Примечание: в случае вырожденного решения одной из задач оба взаимносопряжённых условия выполняются как строгие равенства.
4.2 Экономическая интерпретация и свойства двойственных оценок
Для формулировки свойств двойственных оценок придадим задачам (4.1) – (4.3) и (4.4) – (4.6) конкретный экономический смысл.
Прямая задача
Пусть в производстве n видов продукции используется m видов ресурсов. Известны величины aij , характеризующие нормы расхода каждого вида
34
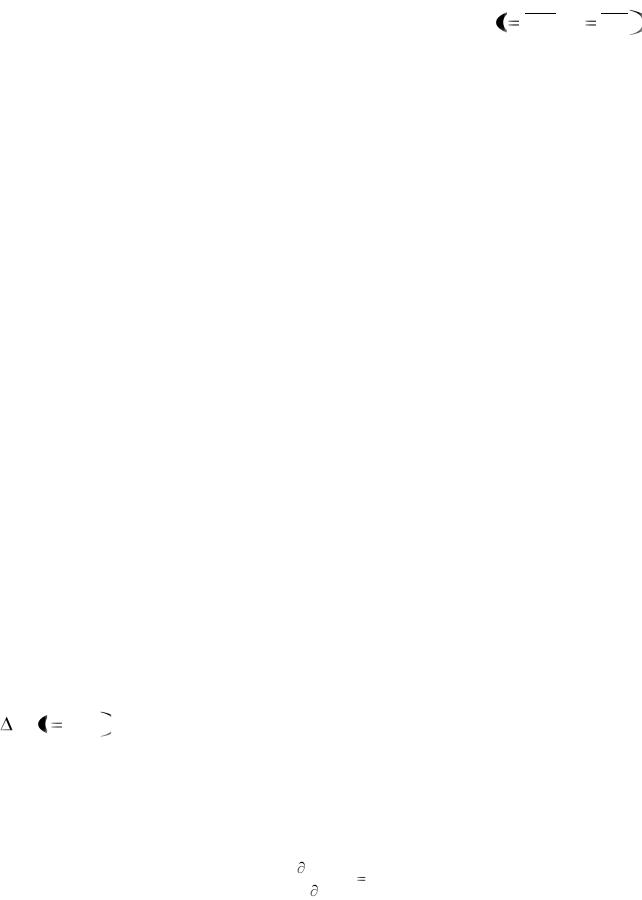
ресурса на производство единицы каждого вида продукции i 1, m, j 1, n . Найти хj – план производства каждого вида продукции, при котором расходы ресурсов не превышали бы имеющихся запасов (bi), a общий доход (Z) от реализации произведённой продукции был бы максимальным.
Двойственная задача
Найти уi – оценки единицы каждого вида ресурсов, минимизирующих суммарную оценку ресурсов, при условии, что оценка ресурсов, необходимых для производства единицы каждого вида продукции, была бы не меньше цены единицы соответствующей продукции. уi – оценка i-ro ресурса с точки зрения его лимитированности в оптимальном плане (теневая цена i-ro ресурса).
Свойство 1. Оценка как мера влияния ограничения на оптимальное значение целевой функции. Это свойство показывает ещё одну связь между переменными прямой и двойственной задач. Поясним это подробнее.
Пусть х* = (х1*, х2*, ..., хj*, ... , хn*) – оптимальное решение прямой задачи, а у* = (у1*, у2*, ..., уi*, ..., уm*) – оптимальное решение двойственной задачи:
Zmax = С1x1* + |
... + Сjxj* + |
... + СnХn*; |
Wmin = b1y1* + ... |
+ biyi* + ... |
+ bmym*. |
На основании первой теоремы |
двойственности (Zmax = Wmin) можно |
|
записать
С1х1* + ... + Сjxj* + ... + Сnхn* = b1у1* + ... + biуi* + ... + bmym*.
Отсюда следует, что
Zmax = b1у1* + ... + biуi* + ... + bmym*.
Поставим вопрос: как изменится величина Zmax, если в исходной задаче увеличить свободный член b в i-м ограничении-неравенстве на величину
|
|
|
|
bi |
i 1, m . |
||
|
Величина Zmax, рассматриваемая теперь как функция переменных |
||
b1, |
b2, ..., bi, ..., bm, получит приращение ∆Zmax. |
||
Частные производные этой функции по любому из этих аргументов (при условии неизменности остальных) имеют вид
Zmax |
yi . |
|
bi |
||
|
Учитывая, что функция Zmax линейная, получим
∆Zmax = yi ∙ ∆bi,
35

т.е. при увеличении объёма i-гo ресурса на единицу (∆bi = 1) оптимальное значение целевой функции увеличится на оценку единицы этого ресурса. Если же объём i-гo ресурса изменить на k единиц, то целевая функция изменится на величину k ∙ уi* при условии, что это изменение не выйдет за границы устойчивости двойственных оценок.
Свойство 2. Оценка как мера дефицитности ресурса. Это свойство
следует из теоремы 2. Если уi* = 0, то из (4.9) следует, что a |
x* |
b , т.е. |
ij |
j |
i |
j |
|
|
i-й ресурс не полностью используется в оптимальном плане и его оценка равна нулю. В соответствии с 1-м свойством, увеличение объёма этого ресурса не приведёт к увеличению объёма выпускаемой продукции. Такой ресурс будем называть недефицитным (нелимитирующим). Для недефицитного ресурса значение соответствующей балансовой переменной показывает его остаток
после выполнения оптимального плана. Если |
уi* > |
0, то из |
(4.8) имеем |
||
a |
x* |
b , т.е. если i-й ресурс полностью расходуется в оптимальном плане, |
|||
ij |
j |
i |
|
|
|
j |
|
|
|
|
|
то его |
оценка положительна. Такой ресурс |
будем |
называть |
дефицитным |
|
(лимитирующим). Чем больше оценка ресурса, тем он дефицитнее с точки зрения его вклада в результат производства. Величина, на которую увеличивается значение целевой функции при увеличении количества лимитирующего ресурса на единицу, называется оценкой ресурса или его теневой ценой. Теневая цена ресурса – это оценка единицы данного ресурса в оптимальном решении.
Свойство 3. Оценка как мера эффективности выпускаемой продукции. Это свойство также следует из теоремы 2. Пусть хj* > 0. Это означает, что
продукция |
вида |
j |
производится в оптимальном плане. Из (4.11) имеем |
aij yi* |
C j , |
т.е. |
оценка ресурсов на производство единицы j-й продукции |
i |
|
|
|
равна стоимости единицы этой продукции. Такую продукцию будем считать
рентабельной. Если хi* = 0, то из (4.10) следует, что |
a |
y* |
C |
j |
, т.е. |
|
ij |
i |
|
|
|
|
i |
|
|
|
|
продукция j-го вида в оптимальном плане не производится, потому что аналогичная оценка ресурсов превышает цену единицы этой продукции. Такую продукцию будем считать нерентабельной.
36
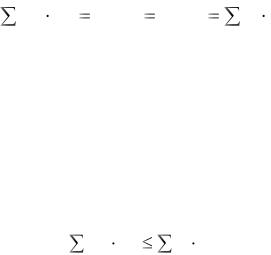
Свойство 4. Оценка как средство балансировки затрат и результатов в оптимальном плане. Это свойство следует из условия (4.7) теоремы 1:
C j x*j Zmax Wmin |
bi yi*. |
j |
i |
Левая часть этого равенства означает стоимость произведённой продукции, т.е. результат производства, а правая – оценку используемых ресурсов, т.е. затраты экономической системы. Следовательно, в оптимальном плане результаты производства балансируются затратами системы на это производство. В случае неоптимальности плана по известной теореме линейного программирования
C j x j |
bi yi , |
j |
i |
т.е. для произвольного плана задачи результат не больше затрат на производство.
4.3 Анализ чувствительности модели
В большинстве случаев принятия решений полезно составить предварительный план действий, чтобы проанализировать, какое воздействие на принятое решение окажут изменения, вносимые в исходную задачу. Большое значение в линейном программировании имеет анализ чувствительности модели. Этот метод позволяет учесть:
–воздействие дополнительного количества лимитирующего ресурса;
–воздействие дополнительного количества нелимитирующего ресурса;
–воздействие изменений в коэффициентах целевой функции.
Итоговая симплексная таблица при решении задачи линейного программирования содержит оптимальное значение целевой функции, значения основных и балансовых переменных. Последние, как известно, соответствуют остаткам ресурсов. Кроме того, в ней указываются оценки (теневые цены) ресурсов. Информацию итоговой таблицы симплексного метода можно использовать также в анализе чувствительности модели, чтобы выявить общее воздействие изменений в запасах лимитирующих ресурсов и в коэффициентах целевой функции на значение целевой функции.
При определении интервалов изменения коэффициентов целевой
37
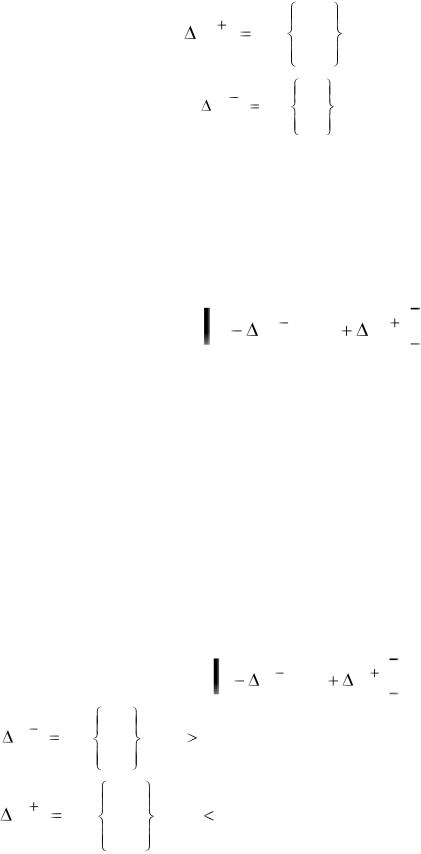
функции необходимо вычислить пределы увеличения и уменьшения этих коэффициентов по формулам
( ) |
|
yi* |
|
|
, для dpi < 0; |
||
С p |
min |
|
|
|
|
||
d pi |
|
|
|||||
|
|
|
|
|
|||
|
|
* |
|
|
|
|
|
( ) |
|
yi |
|
|
|
для dpi > 0, |
|
Сp |
min |
dpi |
, |
||||
|
|||||||
|
|
|
|
|
|||
где yi* – двойственные оценки |
в |
оптимальном решении (элементы Z – |
|||||
строки итоговой симплексной таблицы); |
|
|
|
|
|
||
dpi – элементы строки, соответствующей р-й базисной переменной в итоговой симплексной таблице.
Интервал изменения коэффициента Ср |
при переменной хр |
в целевой |
|
функции имеет вид |
|
|
|
С p |
C(p ); C p |
C(p ) .. |
(4.12) |
Если изменение коэффициента Ср находится в интервале (4.12), то состав базисных переменных и их значения в оптимальном плане не изменятся. Если же изменение Ср не входит в интервал изменения (4.12), то в оптимальном плане изменятся и состав базисных переменных и их значения.
В случае если переменная хk не входит в базис оптимального решения, то интервал изменения коэффициента Сk будет
[0; Сk + уk* ],
где уk* – оценка балансовой переменной хk в оптимальном плане (находится в Z-строке), показывающая превышение оценки затрат ресурсов над ценой
единицы k-й продукции. |
|
|
|
|
|
|
||||
|
Аналогично находятся границы изменения правых частей ограничений |
|||||||||
|
|
|
|
|
b |
b( ) |
; b |
b( ) |
, |
(4.13) |
|
|
|
|
|
k |
k |
k |
k |
|
|
где |
( ) |
|
x*j |
|
|
|
|
|
|
|
|
bk |
min |
|
, d jk |
0, |
|
|
|
|
|
|
d jk |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
bk( ) |
min |
x*j |
|
, d jk |
0. |
d jk |
|
||||
|
|
|
|
|
|
Здесь xj* – значения базисных переменных в оптимальном решении |
|||||
исходной задачи. |
|
|
|
|
|
38
Если изменения правых частей ограничений не выйдут за пределы интервала (4.13), то структура базисных переменных окажется той же, что и в оптимальном решении, а их значения изменятся. При этом оценки оптимального плана (значения yi* в Z-строке) не изменятся и их можно использовать для оценки изменённой целевой функции.
4.4 Свойства двойственных оценок для различных критериев оптимальности
Рассмотрим экономический смысл двойственных оценок (оценок оптимального плана) на примере экономико-математической задачи наилучшего использования ресурсов (в частности, фонда времени работы производственного оборудования), формулируемой с разными критериями оптимальности: максимум прибыли (вариант Р), минимум себестоимости (вариант С) и максимум выпуска продукции в заданном ассортиментном соотношении (вариант А).
Рассмотрим последовательно формулировки прямых и двойственных задач для вариантов Р, С и А и проанализируем экономические свойства двойственных оценок в каждом случае.
Введём обозначения:
aij s – (станко-час/шт.) – норма затрат станочного времени по группе
оборудования i на изготовление продукции j по технологическому способу s;
bi (станко-час) – располагаемый фонд станочного времени по группе оборудования i;
xjs (шт.) – интенсивность способа s, с помощью которого производится продукция j;
PJS (руб./шт.) – прибыль от реализации единицы продукции j по способу s; Мj (шт.) – производственная программа выпуска j-й продукции;
Cjs (руб./шт.) – себестоимость единицы продукции j, производимой по способу s.
39

|
|
|
|
|
|
|
|
|
|
Задача на максимум прибыли (max P) |
|
|
|
|
||||||||||
|
Прямая задача |
|
|
|
|
|
|
|
|
Двойственная задача |
||||||||||||||
n |
rj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
as |
xs |
|
|
|
|
|
|
|
; |
(4.14) |
u |
0; i |
1, |
m; |
|
|
|
(4.14а) |
|||||
|
|
b , |
i |
1, m |
|
|||||||||||||||||||
|
ij |
|
j |
|
i |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
j |
1 s 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xs |
|
|
|
|
|
|
|
; |
(4.15) |
a s |
|
|
P s , |
|
|
|
, j |
|
; (4.15а) |
|||||
0, s |
1, |
r , j |
|
1, n |
|
|
|
|
|
|
||||||||||||||
|
u |
i |
s 1, r |
j |
1, n |
|||||||||||||||||||
j |
|
|
|
i |
|
|
|
|
|
|
|
ij |
|
j |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
max P |
|
|
Ps |
xs |
; |
|
|
|
(4.16) |
min G |
|
b u . |
|
|
|
(4.16а) |
||||||||
|
|
|
|
|
j |
j |
|
|
|
|
|
|
|
|
|
i |
|
i |
|
|
|
|
||
|
|
j s |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
||
Прямая
n |
rj |
xs |
|
as |
|
|
ij |
j |
j |
1 s 1 |
|
Задача на минимум себестоимости (min С) |
|
|||||
задача |
Двойственная задача |
|
||||
|
|
|
|
|
|
|
b , i |
|
; (4.17) |
u 0; i 1, m; |
(4.17а) |
||
1, m |
||||||
i |
i |
|
||||
xsj 0, |
|
|
|
|
j |
|
|
; |
(4.18) |
||
s 1, |
ri , |
1, n |
|||||||||
xsj |
|
|
|
|
|
|
|
||||
M j , |
|
j |
1, n ; |
(4.19) |
|||||||
min C |
C |
j |
|
x |
j |
; |
|
|
|
(4.20) |
|
|
|
|
|
|
|
|
|
|
|
||
j
|
a s |
|
|
C s , s |
|
|
|
|
|
|
|
; |
(4.18а) |
|||
j |
u |
i |
1, r |
j |
, |
j |
1, n |
|||||||||
ij |
|
j |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
j |
0 j |
1, n ; |
|
|
|
|
|
|
|
|
(4.19а) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
m |
|
|
|
|
||
|
max R |
|
M |
j |
|
j |
|
|
b u . |
(4.20а) |
||||||
|
|
|
|
|
|
|
|
|
i |
|
i |
|
||||
|
|
|
j |
1 |
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
Задача на максимум выпуска продукции (max A) |
|
|||||
|
Прямая задача |
Двойственная задача |
|
|||||||
n |
rj |
|
|
|
|
|
|
|
|
|
|
a s |
|
|
b , i |
|
; (4.21) |
u 0; i 1, m; |
(4.21а) |
||
|
x |
j |
1, m |
|||||||
|
ij |
|
i |
i |
|
|||||
j |
1 s |
|
|
|
|
|
|
|
|
|
xs |
|
|
|
|
|
|
|
|
|
|
|
|
0, s |
1, |
r , |
j 1, n ; |
(4.22) |
||||||||
j |
|
|
|
|
i |
|
|
|
|
|
|
|
rj |
|
|
|
|
|
|
|
|
|
|
|
|
|
x j |
|
|
|
|
|
|
|
|
|
|
|
s 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
0, |
j |
1, n ; |
(4.23) |
|||||||
|
|
|||||||||||
k j |
|
|
|
|
|
|
|
|
|
|
||
|
a s |
|
|
|
|
|
, j |
|
; (4.22а) |
j |
u |
i |
0, s 1, r |
j |
1, n |
||||
ij |
|
|
|
|
|
|
|||
|
|
|
|
|
j |
0 j 1, n ; |
(4.23а) |
||
|
|
|
|
|
Z 0; |
(4.24) |
jk j |
1; |
(4.24а) |
|
|
j |
|
|
max A Z ; |
(4.25) |
min D |
b u . |
(4.25а) |
|
|
|
i i |
|
i
40
