
5576
.pdf
Полученная матрица содержит седловую точку
max min aij |
max(1, 0) |
1, |
|
i |
j |
|
|
min max aij |
min (1, 4) |
1, |
|
j |
i |
j |
|
α = β = 1 = а11.
Поэтому решение первоначальной игры, заданной матрицей P3,
имеет вид |
Х * |
|
1 |
, |
|
1 |
, |
|
1 |
, 0, 0 , |
У * |
|
1 |
, |
1 |
, 0, 0 , т.к. стратегии А1, А2, |
А3 |
|
|
|
|
|
|
|
|
||||||||||
|
|
3 |
3 |
3 |
|
2 |
|
2 |
|
|
|||||||
для игрока А и стратегии В1, В2 |
для игрока В чистые и равноправные. |
||||||||||||||||
Стратегии |
А4, |
А5 |
|
и |
|
В3, В4 |
не |
применяются. Цена игры равна |
1. |
||||||||
Оптимальной для игрока А является комбинация стратегий А1, А2, А3, а для игрока В – комбинация стратегий В1 и В2. Вероятность применения стратегий А1, А2 и А3 равны между собой (Σ рi = 1). Аналогично для второго игрока, Σ qj = 1.
Рассмотрим простейший случай конечной игры 2х2, в которой каждый игрок имеет две стратегии. Платёжная матрица игры
Ра11 а12 . Если такая игра имеет седловую точку, то оптимальное
а21 а22
решение – это пара чистых стратегий, соответствующих этой точке. При отсутствии седловой точки игра в соответствии с основной теоремой теории игр имеет оптимальное решение, определяемое парой смешанных
стратегий S*A |
( p1*, p2* ) и SB* (q1*, q2* ) . |
Для того |
чтобы их найти, воспользуемся теоремой об активных |
стратегиях. Если игрок А придерживается своей оптимальной стратегии
S*A , то его средний выигрыш будет равен цене игры v при любой активной стратегии игрока В. Для игры 2х2 любая чистая стратегия противника является активной, если отсутствует седловая точка. Выигрыш игрока А (проигрыш игрока В) – случайная величина, математическое ожидание (среднее значение) которой является ценой игры. Поэтому средний выигрыш игрока А (оптимальная смешанная стратегия) будет равен v и для первой и для второй стратегий.
Средний выигрыш игрока А, если он использует оптимальную
91

смешанную стратегию |
* |
A1 |
A2 |
, а игрок В – чистую стратегию В |
|
S A |
p* |
p* |
1 |
|
|
1 |
2 |
|
(это соответствует первому столбцу матрицы Р), равен цене игры v:
|
a |
p* |
a |
21 |
p* |
|
v . |
|
||||
11 |
1 |
|
2 |
|
|
|
|
|||||
Тот же средний выигрыш получит игрок А, если 2-й игрок применяет |
||||||||||||
стратегию В2, т.е. a12 p1* a22 p2* |
|
v . Учитывая, что p1* p2* |
1, получаем |
|||||||||
систему уравнений для определения оптимальной стратегии |
S*A и ценой |
|||||||||||
игры v: |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
p* |
|
a |
21 |
p* |
v, |
|
|||
11 |
1 |
|
|
|
2 |
|
|
|
||||
|
a12 p1* |
|
a22 p2* |
v, |
(7.7) |
|||||||
|
p* |
p* |
|
|
1. |
|
|
|
|
|||
1 |
|
2 |
|
|
|
|
|
|
|
|
||
Решая эту систему, получим оптимальную стратегию |
|
|||||||||||
p1* |
|
|
a22 |
a21 |
|
|
, |
(7.8) |
||||
|
|
|
|
|
|
|||||||
|
a11 |
|
a22 |
|
a12 |
|
a21 |
|
||||
|
|
p2* |
|
|
|
a11 |
|
a12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a11 |
|
a22 |
|
a12 |
a21 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
и цену игры |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
a11 |
a22 |
a12 a21 |
. |
|
|
|
|
|
(7.9) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
a11 |
a22 |
a12 |
a21 |
|
|
|
|
|
|
|||||||
Составляя аналогичную систему уравнений, можно найти |
|||||||||||||||||||
оптимальную стратегию для игрока В: |
|
|
|
|
|
|
|
|
|
|
|||||||||
q* |
|
a22 |
|
a12 |
|
|
, q* |
|
|
|
|
a11 |
a21 |
|
. |
(7.10) |
|||
1 |
a11 |
a22 |
|
a12 |
|
2 |
|
a11 |
a22 |
a12 |
a21 |
|
|
||||||
|
|
a21 |
|
|
|
||||||||||||||
Пример 7.3.Найти решение игры, заданной матрицей P4 |
1 |
3 . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
Решение. |
|
max(1, 1) |
1; |
|
min(2, |
3) |
2. Матрица |
не |
имеет |
||||||||||
|
|
i |
|
|
|
|
|
|
j |
|
|
|
|
|
|
||||
седловой точки. По формулам (7.8 – 7.11) находим оптимальные стратегии и цену игры:
92
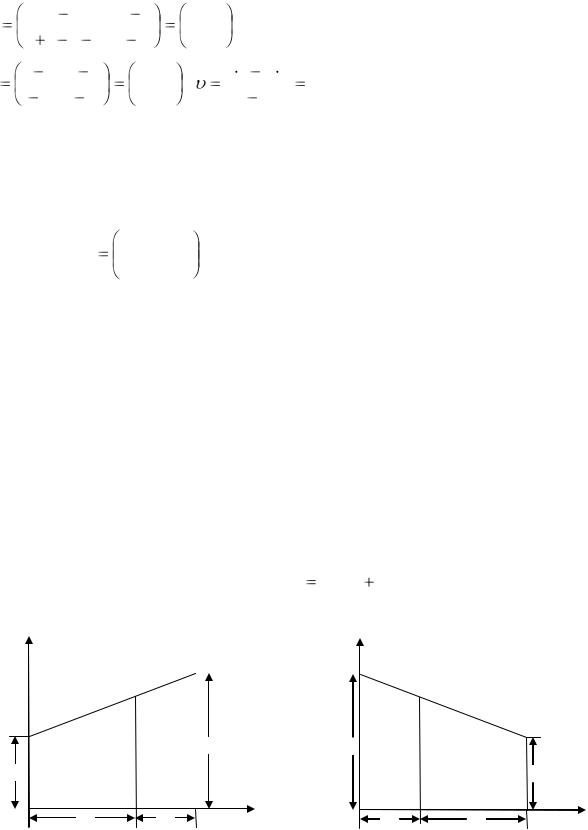
p* |
|
|
1 2 |
|
|
; |
1 3 |
|
|
|
1 |
; |
2 |
, |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
1 |
|
3 |
2 |
3 |
|
|
|
|
|
3 |
3 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
q* |
1 3 |
; |
1 2 |
|
|
2 |
; |
1 |
, |
|
|
|
|
1 1 2 3 |
|
5 |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
3 |
|
|
3 |
|
|
|
3 |
3 |
|
|
|
3 |
3 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
7.4 Геометрическая интерпретация игр 2х2
Игру 2х2 можно решить графическим методом.
Пусть Р |
а11 |
а12 . |
|
а21 |
а22 |
На оси абсцисс (рисунок 7.1) отложим единичный отрезок А1А2. Точка А1 (х = 0) изображает стратегию А1, а все промежуточные точки этого отрезка – смешанные стратегии SA первого игрока, причём расстояние от SA до правого конца отрезка – это вероятность р1 стратегии А1, расстояние до левого конца – вероятность р2 стратегии А2.
На перпендикулярных осях I – I и II – II откладываем выигрыш при стратегиях А1 и А2 соответственно. Если 2-й игрок примет стратегию В1, то она даёт выигрыш а11 и а21 на осях I – I и II – II, соответствующие стратегиям А1 и А2. Обозначим эти точки на осях I – I и II – II буквой В1. Средний выигрыш v1, соответствующий смешанной стратегии SA, определяется по формуле математического ожидания v1 а11р1 а21р2 и равен ординате точке М, которая лежит на отрезке В1В1 и имеет абсциссу SA (рисунок 7.1).
|
у |
|
|
|
|
|
|
|
|
у |
|
|
|
||||
|
|
|
|
|
В1 |
|
II |
I |
|
|
|
В2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
I |
М1 |
|
|
|
|
|
|
|
|
|
|
М2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
В1 |
|
|
|
|
|
|
|
|
|
|
|
|
II |
В2 |
|
|
|
|
|
|
|
|
|
а21 |
|
а12 |
|
|
||||||
|
|
|
|
V1 |
|
|
|
V2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а11 |
|
|
|
|
|
|
|
|
|
|
|
|
а22 |
|
|||
|
|
|
|
SA |
|
|
|
|
|
|
|
|
|
|
SA |
|
|
|
|
|
р2 |
р1 |
|
|
|
|
|
|
|
|
|
р2 |
р1 |
|
|
А1 |
|
|
|
х |
|
|
|
|
|
|
х |
||||||
|
|
|
|
|
|
|
|
I |
|
II |
|||||||
|
I |
|
|
|
|
А2 |
|
|
|
|
|
||||||
|
|
|
II |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Рисунок 7.1 |
|
|
|
|
|
|
Рисунок 7.2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Аналогично строим отрезок В2В2, соответствующий применению вторым |
|
||||||||||||||||
игроком |
стратегии |
В2 (рисунок 7.2). |
При этом |
средний выигрыш |
|
||||||||||||
93
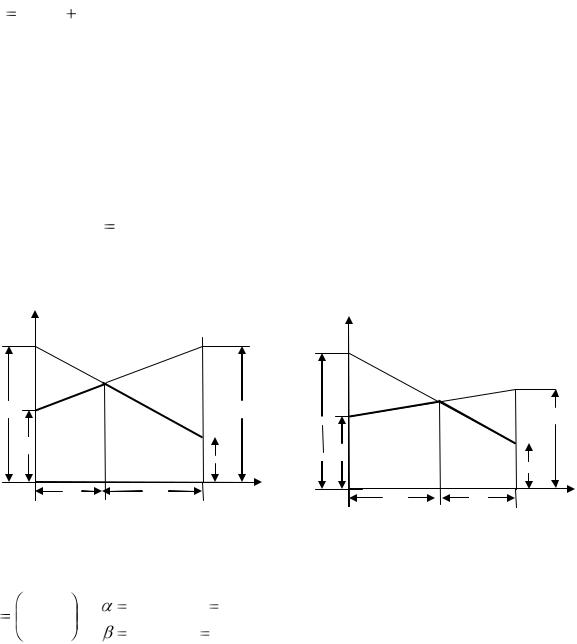
v2 a12 p1 a22 p2 – ордината точки М2.
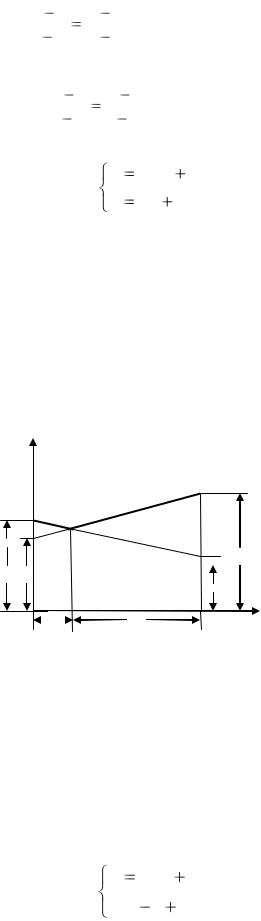
В соответствии с принципом минимакса оптимальная стратегия S*A такова, что минимальный выигрыш игрока А (при наихудшем поведении игрока В) обращается в максимум. Ординаты точек, лежащих на ломаной (рис. 7.3), показывают минимальный выигрыш игрока А при использовании им любой смешанной стратегии (на участке B1N – против стратегии B1, на участке NB2 – против стратегии В2). Оптимальную стратегию S*A ( p1*, p2* ) определяет точка N, в которой минимальный выигрыш достигает максимума. Её ордината равна цене игры v. На рисунке 7.3 обозначены также верхняя и нижняя цены игры α и β.
|
у |
|
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
I |
|
|
|
В1 |
II |
|
|
|
|
|
|
|||
|
В2 |
|
|
|
I |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
В2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
II |
|
В1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
а12 |
|
|
|
|
|
|
β=а21 |
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а21=2 |
||||
|
|
В1 |
|
|
|
|
В2 |
|
а12=3 |
|
|
|
|||
|
|
|
|
|
|
|
В1 |
|
|
В2 |
|||||
|
а11 |
|
|
|
V |
|
|
|
|
|
|
|
|||
|
|
|
|
|
a=а22 |
|
а11=1,5 |
|
V |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
* |
|
|
|
|
|
а22=1 |
||||
|
|
|
|
|
S А |
|
|
|
|
|
S*А |
|
|||
|
|
|
р2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
А1 |
|
|
|
р 1 |
II |
х |
А1 |
р*2 |
р*1 |
|
|
х |
||
|
I |
|
|
|
|
|
|
|
|
|
I |
|
А2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 7.3 |
|
|
|
|
Рисунок 7.4 |
|
|
|
|||
|
Пример 7.4. Решить графически игру, заданную платёжной матрицей |
||||||||||||||
P |
1,5 |
3 |
, |
max(1,5; 1) |
1,5, |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
1 |
min(2; 3) |
2. |
|
|
|
|
|
|
|
||||
Решение. Откладываем на оси абсцисс (рисунок 7.4) единичный отрезок А1А2. На вертикальной оси I – I откладываем отрезки a11 = 1,5, соответствующий стратегии В1, и а12 = 3, соответствующий стратегии В2. На вертикальной оси II – II отрезок а21 = 2, соответствующий стратегии В1, отрезок а22 = 1 соответствует стратегии В2. Нижняя цена игры α = а11 = 1,5. Верхняя цена игры β = а21 = 2, седловая точка отсутствует. Из рисунка 7.4 видно, что абсцисса точки N определяет оптимальную стратегию S*A , а ордината – цену игры v. Точка N является точкой пересечения прямых В1В1 и В2В2.
Уравнение прямой В1В1, проходящей через точки (0; 1,5) и (1; 2):
94
|
x |
0 |
|
y |
1,5 или у = 0,5х + 1,5. |
||||
|
1 |
0 |
|
2 |
1,5 |
|
|
|
|
Уравнение прямой В2В2, проходящей через точки (0; 3) и (1; 1): |
|||||||||
|
|
x |
0 |
|
y |
3 |
или у = 2х + 3. |
||
|
|
1 |
0 |
|
1 |
3 |
|||
|
|
|
|
|
|||||
Точка пересечения прямых является решением системы |
|||||||||
|
|
|
|
|
y |
|
0,5x |
1,5, |
|
|
|
|
|
|
y |
|
2x |
3 |
|
или х = 0,6, у = 1,8, т.е. N(0,6; 1,8). |
|
|
|
|
|||||
Таким образом, р1* = 0,6, |
р2* = 1 – 0,6 = 0,4, оптимальная стратегия |
||||||||
SА* = (0,6; 0,4), цена игры v = 1,8.
Геометрически можно также определить оптимальную стратегию игрока В, если поменять местами игроков А и В и вместо максимума
нижней границы |
А2 М |
А1 в соответствии с принципом минимакса |
|||
(рисунок 7.5) рассмотреть минимум верхней границы. |
|||||
|
у |
|
|
|
|
|
I |
|
|
|
|
|
|
|
II А1 |
|
|
|
А2 |
М |
|
|
|
|
|
|
|
|
|
а21=2 |
А1 |
|
А2 |
а21=3 |
|
|
|
|
|
||
а11=1,5 |
V |
|
|
|
|
|
0 |
* |
а22=1 |
|
|
|
S В |
|
|
|
|
|
q*2 |
q*1 |
II |
|
х |
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 7.5 |
|
|
|
Абсцисса точки М определяет q2* в оптимальной стратегии игрока В, ордината этой точки – цена игры. Прямая А1А1, проходящая через точки (0; 1,5) и (1; 3) удовлетворяет уравнению у = 1,5х + 1,5.
Прямая А2А2, проходящая через точки (0; 2) и (1; 1), удовлетворяет уравнению у = – х + 2. Координаты точки пересечения М являются решением системы уравнений
у 1,5х 1,5,
у 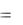 х 2.
х 2.
95
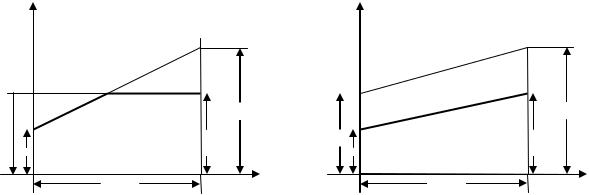
Решив систему, получаем х=0,2; у= 1,8, т.е. q2* = 0,2; q1* = 1 – q2*=0,8,
υ = у = 1,8, SВ* = (0,8; 0,2).
Из решения примера 7.4 следует, что геометрически можно определять оптимальную стратегию как игрока А, так и игрока В; в обоих случаях используется принцип минимакса, но во втором случае строится не нижняя, а верхняя граница выигрыша и на ней определяется не максимум, а минимум.
Если платёжная матрица содержит отрицательные числа, то для графического решения задачи нужно перейти к новой матрице с неотрицательными элементами; для этого к элементам исходной матрицы достаточно добавить соответствующее положительное число. Решение игры при этом не изменится, а цена игры увеличится на это число. В примере 7.4 платёжная матрица не имела седловой точки (α ≠ β). При наличии седловой точки графическое решение дают варианты, изображённые на рисунках 7.6 и 7.7.
|
у |
|
|
|
|
|
у |
|
|
|
|
|
||||
|
|
|
I |
В1 |
|
II |
|
|
|
|
|
I |
В2 |
|
II |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
В2 |
N |
В2 |
|
|
|
|
|
В2 |
|
В1 |
|
||
|
|
|
|
|
|
а21 |
|
|
|
|
|
|
|
|
а22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
α=β= |
|
|
|
|
|
В1 |
|
α=β= |
|
а12 |
В1 |
|
|
||||||
|
а11 |
* |
=υ=а22 |
|
|
а11 |
|
|
=υ=а21 |
|
||||||
|
|
|
|
S А |
|
|
|
|
|
|
|
|
|
|
|
|
|
А1 |
р*2=1 |
А2 |
х |
|
А1 |
|
р*2=1 |
А2 |
х |
||||||
|
|
I |
|
|
II |
|
|
|
I |
|
|
|
II |
|
||
|
|
|
|
Рисунок 7.6 |
|
|
|
|
|
|
|
|
Рисунок 7.7 |
|
|
|
На рисунке 7.6 наибольшей ординатой на ломаной B1NB2 обладает точка B2, поэтому оптимальной стратегий является чистая стратегия А2 для игрока А (B2 – для игрока В), т.е. оптимальное решение: SА* = (0; 1), SВ* = (0; 1). Игра имеет седловую точку а22 = v.
Чистая стратегия B2 (рисунок 7.7) не выгодна для игрока В, поскольку при любой стратегии игрока А она даёт последнему больший выигрыш, чем чистая стратегия B1. На основании принципа минимакса выделим прямую B1B1 и на ней точку B1 с наибольшей ординатой на оси I – I.
96

Чистая стратегия А2 является оптимальной для игрока А, а чистая стратегия игрока B1 – для игрока В. Оптимальное решение: SА* = (0; 1), SВ* = (1; 0), цена игры v = а21 = α = β, т.е. имеется седловая точка.
Графический метод можно применять при решении игры 2хn и mx2.
7.5 Приведение матричной игры к задаче линейного программирования
Пусть игра задана платёжной матрицей Р размером m x n:
|
а11 |
a12 |
... |
a1m |
|
|
Р |
а21 |
a22 |
... |
a2m |
. |
|
... ... ... ... |
||||||
|
|
|||||
|
аm1 |
am2 |
... |
amn |
|
|
Матрица Р не имеет седловой точки, поэтому решение игры представлено в смешанных стратегиях.
Игрок А обладает стратегиями А1, А2, ..., Аm, игрок В – стратегиями В1, В2, ..., Вn. Необходимо определить оптимальные стратегии SА*=(р1*, р2*, ..., рm*) и SВ*=(q1*, q2*, ..., qn*), где рi*, qj* – вероятность применения соответствующих чистых стратегий Аi, Вj, причём
р1* + р2* + ... + рm* = 1, q1* + q2* + qn* = 1.
Оптимальная стратегия SА* удовлетворяет следующему требованию. Она обеспечивает игроку А средний выигрыш, не меньший, чем цена игры, при любой стратегии игрока В и выигрыш, равный цене игры v, при оптимальной стратегии игрока В. Величина v (цена игры) неизвестна. Будем считать v > 0, этого можно добиться, прибавляя ко всем элементам матрицы некоторое положительное число. Если игрок А применяет смешанную стратегию SА* = (р1*, р2*, ..., рm*) против любой чистой стратегии Вj игрока В,
то он получат средний выигрыш, или математическое ожидание выигрыша
аj = a1j p1 + a2j p2+ … + amj pm, j 1, n .
Для оптимальной стратегии SА* все средние выигрыши не меньше цены игры, поэтому получаем систему неравенств:
97

|
|
a11p1 |
a21p2 |
... am1 pm |
v, |
|
|
|
||||||
|
|
a12 p2 |
a22 p2 |
... |
am2 pm |
v, |
(7.11) |
|
||||||
|
...................................................... |
|
||||||||||||
|
|
|
|
|||||||||||
|
|
a1n p2 |
a2n p2 |
... |
amn pm |
v. |
|
|
|
|||||
Разделим каждое неравенство на v > 0. Введём новые переменные |
|
|
||||||||||||
|
х1 |
р1 v, х2 |
р2 v,..., хm |
|
pm v. |
(7.12) |
|
|||||||
Тогда система 7.11 примет вид: |
|
|
|
|
|
|
|
|
||||||
|
|
|
a11x1 |
a21x2 |
... am1xm |
1, |
|
|
|
|||||
|
|
|
a12x2 |
a22x2 |
... am2 xm |
|
1, |
(7.13) |
|
|
||||
|
|
|
...................................................... |
|
|
|
||||||||
|
|
|
a1n x2 |
a2n x2 |
... |
amn xm |
|
1. |
|
|
|
|||
Цель игрока А – максимизировать свой гарантированный выигрыш, |
||||||||||||||
т.е. цену игры v. |
|
|
|
|
|
|
|
|
|
|
|
|||
Разделив на v ≠ 0 равенство р1 + р2 + ... + рm = 1, получаем, что |
||||||||||||||
|
|
|
|
|||||||||||
переменные xi |
i 1, m удовлетворяют условию: х1 + х2 + ... + хm = 1 / v. |
|||||||||||||
Максимизация |
цены |
игры |
v |
эквивалентна |
минимизации |
величины |
1 |
, |
||||||
v |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
поэтому задача может быть сформулирована следующим образом:
|
|
|
|
определить значения переменных xi ≥ 0 i 1, m , так, |
чтобы они |
||
удовлетворяли ограничениям (7.13) и целевая функция |
|
||
Z = x1 + x2 + … + xm |
(7.14) |
||
обращалась в минимум. Это задача линейного программирования. Решая
задачу (7.13) – (7.14), получаем оптимальные значения хi* и величину 1 , v
затем находим рi* = v ∙ хi* и оптимальную стратегию SА* = (р1*, р2*, ..., рm*). Для определения оптимальной стратегии SВ*=(q1*, q2*, ..., qn*) игрок В
стремится минимизировать гарантированный выигрыш, т.е. найти max 1v .
Переменные q1, q2, ..., qn удовлетворяют неравенствам
98

a11q1 |
a21q2 |
... |
a1n xn |
v, |
|
a21q1 |
a22q2 |
... a2nqn |
v, |
(7.15) |
|
...................................................... |
|
||||
am1q1 |
am2q2 |
... |
amnqn |
v |
|
и показывающим, что средний проигрыш игрока В не превосходит цены игры, какую бы чистую стратегию не применял игрок А.
|
|
|
|
|
|
|
|||
Если обозначить yj = qj / v, j |
1, n , |
|
(7.16) |
||||||
то получим систему неравенств |
|
|
|
|
|
|
|||
|
a11y1 |
a12 y2 |
... |
|
a1n yn |
1, |
|
||
|
a21y1 |
a22 y2 |
... |
a2n yn |
1, |
(7.17) |
|||
...................................................... |
|
||||||||
|
am1y1 |
am2 y2 |
... |
amn yn |
1. |
|
|||
|
|
|
|||||||
Переменные yj j 1, n |
удовлетворяют условию у1 + у2 + ... + уn = 1/v. |
||||||||
Таким образом, |
получили |
задачу линейного |
программирования: |
||||||
|
|
|
|
|||
определить значения переменных yj ≥ 0 j |
1, n , которые удовлетворяют |
|||||
системе неравенств (7.17) и максимизирующих линейную функцию |
||||||
|
W = у1 + у2 + ... + уn. |
|
|
|
|
(7.18) |
Решение задачи (7.17) – (7.18) даёт оптимальные значения yj* и |
||||||
величину 1/v, затем |
находим qj* = v ∙ |
yj* |
и оптимальную |
стратегию |
||
SВ*=(q1*, q2*, ..., qn*). При этом цена игры |
|
|
|
|
|
|
|
v = 1/max W = 1/min Z. |
(7.19) |
||||
Рассмотренные |
задачи (7.13), (7.14), |
(7.17) и (7.18) |
являются |
|||
симметричными двойственными задачами. Таким образом, для решения игры нужно решить одну из задач, требующую меньших вычислений, затем найти решение второй с помощью теорем двойственности.
Пример 7.5. Предприятие может выпускать три вида продукции (А1, А2 и А3), получая при этом прибыль, зависящую от спроса, который может быть в одном из четырёх состояний (В1, В2, В3, В4). Дана матрица (таблица 7.4), её элементы aij характеризуют прибыль, которую получит предприятие при выпуске i-й продукции с j-м состоянием спроса.
Определить оптимальные пропорции в выпускаемой продукции, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределённым.
99
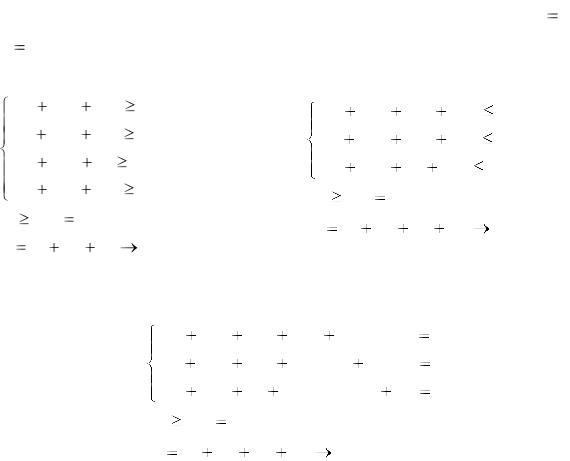
Решение. Задача сводится к игровой модели, в которой игра предприятия А против спроса В задана платёжной матрицей (таблица 7.4). Таблица 7.4 – Платёжная матрица
|
В1 |
В2 |
В3 |
В4 |
А1 |
4 |
3 |
4 |
2 |
|
|
|
|
|
А2 |
3 |
4 |
6 |
5 |
|
|
|
|
|
А3 |
2 |
5 |
1 |
3 |
Определим нижнюю и верхнюю цены игры: α = max(2, 3, 1) = 3, β = min(4, 5, 6, 5) = 4. Так как α ≠ β, то матрица не имеет седловой точки и оптимальное решение следует искать в смешанных стратегиях игроков
SА* = (р1, р2, р3) и SВ*=(q1, q2, q3, q4). Обозначим xi = pi/v, yj |
|
|
|
||||||||||||||||||||||
= qj/v, i 1, m , |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
j |
1, n . Составим симметричные двойственные задачи. |
|
|
|
|
||||||||||||||||||||
|
|
Задача 1 |
|
|
|
|
|
|
|
|
|
|
|
Задача 2 |
|
|
|
|
|||||||
4х1 |
3х2 |
2х3 |
1, |
|
|
|
|
|
4 у 3у |
2 |
|
4 у |
2 у |
4 |
1, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|||
3х1 |
4х2 |
5х3 |
1, |
|
|
|
|
|
3у 4 у |
2 |
|
6 у |
5 у |
4 |
1, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|||
4х1 |
6х2 |
х3 |
1, |
|
|
|
|
|
2 у1 |
5 у2 |
у3 |
3у4 |
|
1, |
|
|
|||||||||
2х1 |
5х2 |
3х3 |
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
у j |
0, |
i 1, 4, |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
xi |
0, |
|
i 1, m, |
|
|
|
|
|
|
W |
y1 |
y2 |
|
y3 |
y4 |
|
max. |
||||||||
Z |
|
x1 |
|
x2 |
x3 |
min . |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Задачу 2 приведём к канонической: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
4 у1 |
|
3у2 |
4 у3 |
2 у4 |
у5 |
|
|
|
1, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
3у1 |
4 у2 |
6 у3 |
5 у4 |
|
у6 |
|
|
1, |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 у1 |
|
5 у2 |
|
у3 |
3у4 |
|
|
|
|
у7 |
1, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у j |
0, |
i 1, 7, |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
W |
y1 |
y2 |
|
y3 |
y4 |
max. |
|
|
|
|
|
|
|
|
|
||
Решим каноническую задачу симплексным методом в симплексных таблицах (таблица 7.5).
100
