
5576
.pdf
расположения отраслей производителей и отраслей потребителей в налагаемых одна на другую таблицах идентичны. Каждый показатель, представленный в этой части МОБ, имеет двойную смысловую нагрузку: как элемент столбца он выступает в качестве затратной характеристики, как элемент строки – в качестве распределительной. Строки и столбцы “шахматки”, имеющие одинаковые номера, характеризуют процесс производства (столбцы) и распределения (строки) продукции одной и той же отрасли на нужды текущего производственного потребления. Следовательно, в пределах “шахматки” (I квадранта МОБ) отражается внутрипроизводственный оборот (промежуточные затраты – промежуточный выпуск) предметов труда и услуг.
Межотраслевой анализ базируется на использовании статистических таблиц, называемых межотраслевыми, дающих картину народнохозяйственной динамики за определённый период (как правило, за один год), содержание которой составляют связи между отраслями. Рассмотрим общую схему МОБ, которая в стоимостном исчислении состоит из четырёх разделов (квадрантов) (таблица 2.1).
Таблица 2.1 – Таблица межотраслевого баланса
|
|
|
Текущее производственное потребление |
|
Конечный |
Вало- |
||||||
Распределение |
|
|
|
в отраслях |
|
|
продукт |
вой |
||||
продукции |
|
|
|
|
|
|
|
|
|
про- |
||
|
|
|
|
|
|
|
|
|
|
|
|
дукт |
Затраты на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
производство |
1 |
2 |
… |
j |
…. n |
Итого |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Матери- |
|
1 |
x11 |
x12 |
… x1j |
… x1n |
x1j |
|
y1 |
x1 |
||
|
|
2 |
x21 |
x22 … x2j … x2n |
x 2j |
|
y2 |
x2 |
||||
альные |
|
… |
………………I кв.…………………. |
|
II кв. |
|
||||||
|
|
|
|
|||||||||
|
|
i |
xi1 |
xi2 |
… xij |
… xin |
x ij |
|
yi |
xi |
||
затраты |
|
… |
|
|
|
|
|
|
j |
|
|
|
|
………………………………….. |
|
|
|
|
|
||||||
|
|
n |
xn1 |
xn2 … xnj … xnn |
|
|
yn |
xn |
||||
|
|
|
|
|
|
|
|
|
x n j |
|
|
|
|
|
Итого |
x i1 |
x i2 . |
x ij |
x in |
x ij |
|
yi |
x i |
||
|
|
|
|
|
|
i |
|
|
i, j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Условно-чистая |
|
|
|
|
|
|
|
|
|
|
||
продукция |
z1 |
z2 |
III zj |
… zn |
|
z j |
|
IV кв. |
|
|||
Валовой продукт |
x1 |
x2 |
…. xj |
… xn |
x j |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
11
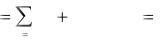
За пределами I квадранта остались и как бы обрамляют его те части налагаемых друг на друга таблиц, в которых отражается использование произведённой продукции на нужды конечного потребления (закупки конечных продуктов – потребительских или инвестиционных) (II квадрант), а также величина стоимости отраслевой продукции, добавленная к стоимости израсходованных в процессе производства сырья, материалов, топлива, энергии, полуфабрикатов и т.п. (созданный национальный доход и амортизация основных фондов (III квадрант).
Квадрант IV расположен на пересечении продолжения строк квадранта III и столбцов квадранта II. В нём детально показывается, как используется национальный доход на потребление и накопление, а также как используются амортизационные отчисления на простое и расширенное воспроизводство. Наряду с этим в квадранте IV отражается частичное перераспределение национального дохода, в результате которого формируются конечные доходы сферы материального производства, непроизводственной сферы и населения.
В I и II квадрантах отражаются важнейшие материально-вещественные взаимосвязи и пропорции национальной экономики, выраженные в стоимостных измерителях: отраслевая и материально-вещественная структура фондов текущего производственного потребления и конечной продукции.
Каждая строка здесь характеризуется следующим балансом:
Выпуск продукции |
= |
Промежуточный спрос + |
Конечный спрос |
|||
или |
|
|
|
|
|
|
n |
|
|
|
|
|
|
xi |
xij |
yi |
(i 1,n ) , |
(2.1) |
||
j |
1 |
|
|
|
|
|
где xi – валовой продукт i-й отрасли;
n – число отраслей в МОБе, т.е. по каждой отрасли объём произведённой продукции равен объёму потреблённой продукции.
В I и III квадрантах находят отражение важнейшие стоимостные пропорции по производству национального продукта. Здесь отражена стоимостная отраслевая структура затрат или структура используемых ресурсов, необходимых для каждой отрасли.
Каждый столбец здесь характеризуется следующим балансом: Расходы отрасли = Промежуточные затраты + Добавленная стоимость, что в математической записи выглядит так:
12
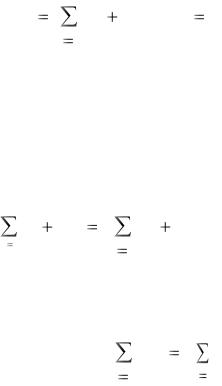
|
n |
|
|
|
|
x j |
xij z j |
( j 1, n). |
(2.2) |
||
i |
1 |
|
|
|
|
Единство материально-вещественного и стоимостного состава валового (совокупного) национального продукта, конечного продукта и национального дохода проявляется в сбалансированности итогов строк и столбцов МОБ: итоги одноимённых строк и столбцов таблицы МОБ равны, т.е. равны выпуск и расходы отрасли:
n |
|
n |
|
j 1 |
xij yi |
xij z j |
( при i = j ), |
i |
1 |
|
|
|
|
а следовательно, общая сумма конечного спроса равна общей сумме добавленной стоимости:
n |
n |
|
yi |
z j . |
(2.3) |
i 1 |
j 1 |
|
Равенство (2.1) называется системой уравнений распределения продукции, равенство (2.2) – системой уравнений производства продукции, а (2.3) – основное балансовое соотношение.
Система показателей III и IV разделов баланса является основой для построения финансовых балансов (или балансов доходов и расходов). Объединение показателей разделов III – IV (по горизонтали) и II – IV (по вертикали) позволяет строить материально-финансовые балансы, характеризующие соответствие денежных доходов населения, государства, организаций и фирм и их материального покрытия.
2.2 |
Исследование и решение системы уравнений |
модели |
межотраслевого баланса
Таблица МОБ позволяет изучать структуру потоков ресурсов, однако для понимания функционирования экономики, в частности эффекта распространения (мультипликации), необходимо сделать ещё один шаг, заключающийся в построении коэффициентов прямых затрат и коэффициентов полных затрат. Будем, следуя автору модели, американскому учёному русского происхождения В. Леонтьеву, считать, что объёмы промежуточного
13

производственного |
потребления |
прямо |
пропорциональны |
объёмам |
|
производства продукции потребляющих отраслей: |
|
||||
|
|
|
|
|
|
|
xij = aij |
xj (i,j = 1, n ) , |
(2.4) |
||
где коэффициентами пропорциональности aij являются коэффициенты прямых материальных затрат, определяемые из соотношений:
|
|
|
|
aij = xij / xj (i,j = 1, n ). |
(2.5) |
||
Из (2.5) следует и смысл этих коэффициентов; |
они показывают объём |
||
материальных ресурсов i-го вида, необходимый для производства единицы валового продукта j-го вида. После подстановки (2.4) в (2.1) получаем
n |
|
|
|
|
|
|
xi |
aij x j |
yi |
(i 1, n ) . |
(2.6) |
||
j |
1 |
|
|
|
|
|
Это и есть система уравнений модели В. Леонтьева “затраты – выпуск”, называемая статической моделью МОБ. Статической она является потому, что отражает производство и основные потоки продукции между отраслями за фиксированный промежуток времени (обычно за год), в течение которого все параметры модели остаются постоянными.
Получив систему уравнений (2.6), мы вплотную подошли к центральному вопросу межотраслевого анализа: как изменится объём валового выпуска i-й отрасли (xi), если при фиксированных коэффициентах прямых затрат aij значение yi изменится на величину yi. Отметим, что соотношение (2.4) предполагает существование производственной функции с неизменным эффектом масштаба (затраты прямо пропорциональны выпуску) и с отсутствием взаимозаменяемости ресурсов (соотношение затрат ресурсов фиксировано и не зависит от уровня выпуска). Кроме того, здесь учитываются только затраты промежуточных продуктов, затраты факторов производства опущены. Для ответа на поставленный вопрос необходимо найти решение xi (i = 1, n ) системы линейных уравнений (2.6) при фиксированных значениях
|
|
|
|
|
|
|
|
|
|
спроса на конечную продукцию yi (i = 1, n ). |
|
|
|
|
|||||
Запишем систему уравнений (2.6) в матричной форме: |
|
|
|||||||
|
|
X = AX + Y , |
|
|
|
(2.7) |
|||
|
x1 |
|
a11 |
a12 ... |
a1n |
|
y1 |
|
|
x |
x2 |
; A |
a21 |
a22 ... |
a2n |
, Y |
y2 |
. |
|
... |
|
|
|
|
... |
||||
|
|
|
|
|
|
|
|
||
|
xm |
|
an1 |
an2 an3 |
ann |
|
yn |
|
|
14

(2.7) является леонтьевской моделью МОБ. Решим это уравнение относительно Х, определив валовой выпуск отраслей, обеспечивающий
заданный уровень спроса Y на конечную продукцию отраслей: |
|
|
X – AX = Y, |
(E – A) X = Y, X = (E – A)-1 Y. |
(2.8) |
Последняя формула, как известно, может быть записана, если существует |
||
обратная матрица к матрице (Е – А). |
|
|
Рассмотрим кратко |
вопрос о существовании и свойствах |
матрицы |
В = (Е – А)-1. Матрица А коэффициентов прямых материальных затрат в случае стоимостного межотраслевого баланса относится к хорошо изученному в математике классу матриц. В силу экономического смысла все диагональные
элементы матрицы А должны быть меньше единицы (aii < 1, i 1,n ), в противном случае производство лишается всякого смысла (если aii>1, то xii >xi).
Кроме того, |
aij |
1 для всех отраслей и |
aij 1, что естественно для |
|
|
|
i |
продуктивной экономики, иначе отрасль будет настолько убыточной, что её убытки перекроют расходы на амортизацию и оплату труда.
Доказано, что перечисленные выше условия для элементов матрицы А являются необходимыми и достаточными, чтобы матрица А и соответствующая ей экономика были продуктивными, т.е. чтобы существовали неотрицательные векторы X 0 и Y 0, такие, что
X – AX = Y.
Из продуктивности матрицы А следует, что существует обратная матрица (Е – А)-1 и все её элементы неотрицательны, а также имеет место разложение:
(Е – |
А)-1 = Е + А + А2+…..+ Аm +…., |
(2.9) |
причём Am 0, при n |
. Стремление матрицы Am к нулевой настолько |
|
быстрое, что уже первых несколько членов этого разложения достаточно для вычисления обратной матрицы с большой точностью. Заметим, что формула
(2.9) часто используется для вычисления обратной матрицы |
большой |
размерности. |
|
Матрица |
|
В = (Е – А) –1 |
(2.10) |
называется обратной матрицей Леонтьева, или матричным мультипликатором, или мультипликатором Леонтьева. Выясним её экономический смысл, для чего (2.8) распишем подробнее (с учётом обозначения (2.10))
15

|
n |
|
|
X = B Y или |
xi |
bij y j . |
(2.11) |
|
j |
1 |
|
откуда |
xi |
bij или |
xi |
bij |
. Отсюда имеем, что bij |
показывает |
|
y j |
y j |
||||||
|
|
|
|
|
потребность в дополнительном валовом выпуске продукции i-й отрасли для производства дополнительной единицы конечной продукции j-й отрасли. Таким образом, bij в сущности есть мультипликатор, показывающий эффект распространения спроса на валовую продукцию, первоначальным источником которого является спрос на конечную продукцию.
Подставим (2.9) в (2.11) и получим:
X = (E – A)-1 Y = (E + A + A2 + …+ Am + …) Y,
откуда X = Y + AY + A2Y +…+ AmY + … .
Итак, валовой выпуск, обеспечивающий производство конечного спроса в объёме Y, состоит из самого конечного спроса Y плюс величины AY, являющейся результатом первичного эффекта распространения, плюс A2Y – вторичного и т.д.
Элементы матрицы В называются коэффициентами полных материальных затрат. С учётом линейности соотношений (2.11) эффект распространения X, вызванный изменением конечного спроса на величину Y рассчитывается как
X = B Y.
Кроме того, говорят, что решение системы уравнений МОБ позволяет определить равновесный выпуск, имея в виду под общим равновесием такое соотношение экономической системы, которое характеризуется равновесием спроса и предложения всех ресурсов.
Как мы видели, равновесный выпуск определяется из системы уравнений распределения продукции (2.1). Система уравнений производства продукции является основой для получения равновесных цен. Равновесные цены позволяют исследовать ценовой аспект эффекта распространения и построить ценовую модель МОБ.
Обозначим vj = zj / xj – величину добавленной стоимости, приходящейся на единицу валовой продукции отрасли и называемой долей добавленной стоимости. Тогда, учитывая, что zj = vj xj , (2.2) перепишем в виде:
16
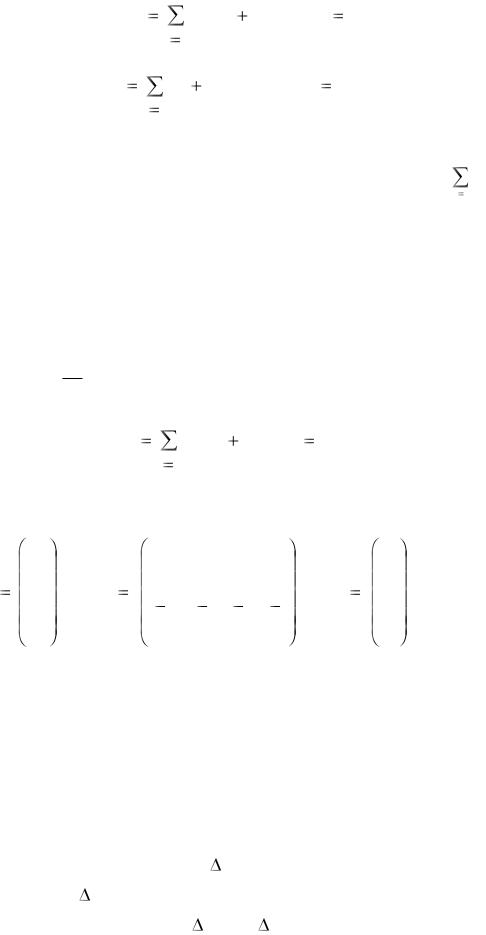
|
|
n |
|
|
|
|
|
|
|
x j |
aij x j |
v j x j , ( j 1, n) , |
|
||||
|
|
i 1 |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
или |
1 |
aij v j , |
( j 1, n). |
(2.12) |
||||
|
i |
1 |
|
|
|
|
|
|
Это выражение описывает формирование цен каждого вида продукции в |
||||||||
|
|
|
|
|
|
|
|
n |
базовом периоде, |
если их принять за единицу. Слагаемое |
aij показывает |
||||||
|
|
|
|
|
|
|
|
i 1 |
возмещение стоимости, а vj – вновь созданную стоимость (с учётом амортизации). Система равенств (2.12) представляет собой модель балансовых цен, на основе которой можно выяснить, как через посредство структуры потребляемых каждой отраслью ресурсов изменяется структура цен при варьировании величины добавленной стоимости.
Если для расчётного периода доля добавленной стоимости будет равна vj, то цены P(j = 1, n ) будут определяться по (2.12) из соотношений
n
|
|
|
|
|
p j |
aij pi v j ( j 1, n ) . |
(2.13) |
||
i1
Вматричном виде эту систему можно переписать как
|
|
|
|
Р = Ат Р + V , |
|
(2.14) |
|||
|
p1 |
|
a11 |
a21 ... |
an1 |
|
|
V1 |
|
где P |
p2 |
; AT |
a12 |
a22 ... |
an2 |
; |
V |
V2 . |
|
|
... |
|
|
|
|
|
|
... |
|
|
pn |
|
a1n |
a2n ... |
ann |
|
|
Vn |
|
Матрица Ат – транспонированная матрица А. |
|
|
|
||||||
|
Решим (2.14) относительно Р. Получим |
|
|
|
|||||
|
|
P – AT P = V ; (E –AT) P = V ; P = (E – AT)-1 V ; |
|
||||||
|
|
P = [(E – AT)-1 ] T V |
или |
|
P = BT |
V |
(2.15) |
||
|
Уравнения (2.13) и (2.14) называют моделью равновесных цен, а матрицу |
||||||||
Вт – ценовым матричным мультипликатором (матричным мультипликатором ценового эффекта распространения).
Эффект распространения Р, вызванный изменением доли добавленной стоимости на V, может быть рассчитан из (2.15) как
P = BT V.
17
2.3Балансы трудовых ресурсов и основных производственных фондов
Все виды затрат в конечном счёте сводятся к затратам труда, труд является единственным источником стоимости, поэтому трудовые показатели МОБ играют важную роль в решении проблемы измерения затрат и результатов национального производства, его эффективности.
Упрощённый межотраслевой баланс труда описывается уравнением
|
|
n |
|
|
L |
t j x j , |
(2.16) |
|
|
j 1 |
|
где tj – коэффициенты прямых затрат труда в |
j-й отрасли; tj = Lj / xj (Lj – |
||
объёмы затрат труда в |
j-й отрасли). |
|
|
Учёт трудовых |
ресурсов |
предполагает |
наравне с решением системы |
уравнений по производству и распределению продукции рассматривать также баланс трудовых ресурсов.
Кроме того, дополним схему МОБ производства и распределения продукции балансом основных фондов
|
n |
|
|
|
|
Ф |
f j |
x j , |
(2.17) |
|
j |
1 |
|
|
где fj – коэффициенты |
прямой фондоёмкости в j-й отрасли; fj = Фj |
/ xj (Фj – |
||
наличие фондов в j-й отрасли). |
|
|
|
|
Баланс основных |
фондов может, |
в |
частности, ограничивать |
объёмы |
выпуска продукции, вместе с тем вектор конечного продукта, включая в себя фонд производственного накопления, является ограничением на возможный прирост основных фондов, поэтому учёт этого баланса также важен в решении
задачи определения сбалансированного выпуска. |
|
|||
В матричной записи (2.16) и (2.17) примут вид |
|
|||
|
|
L = t Х , Ф = f Х . |
|
|
Перепишем их с учётом (2.11), получим |
|
|
||
|
L = t Х = t B Y = |
Y ; |
(2.18) |
|
|
Ф = f Х = f B Y = |
Y , |
(2.19) |
|
где = t B или |
|
n |
|
(2.20) |
k |
t j b jk, |
|
||
|
j |
1 |
|
|
18

= f B или |
|
n |
(2.21) |
k |
f j b jk, |
||
|
j |
1 |
|
Коэффициенты |
k и |
k называются соответственно коэффициентами |
|
полных затрат труда и фондов и показывают, как это следует из (2.20) и (2.21), потребность в соответствующих ресурсах во всех отраслях национальной экономики для производства единицы конечного продукта в k-й отрасли. А (2.18) и (2.19) показывают, что прямые затраты ресурса на выпуск валовой продукции совпадают с их полными затратами на выпуск конечного продукта.
Уменьшение полных затрат труда на единицу продукции является обобщающим показателем роста производительности труда, эффективности общественного производства. Аналогично и для затрат основных фондов. Поэтому коэффициенты полных затрат труда и фондов являются ценным инструментом при сравнении эффективности различных вариантов модельных расчётов.
Здесь для простоты изложения трудовые ресурсы и основные фонды не разделялись по их видам. Учёт последнего приводит к более сложным моделям. Рассмотрим одну из них.
|
|
2.4 Расширенная модель МОБ |
|
|
|
|
|
|
|
|
Выделим из вектора конечного |
продукта фонд производственного |
|||||
накопления в виде прироста основных фондов Ф, тогда |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Y = Y |
+ |
Ф, |
|
|||
где Y – конечный продукт статистической модели МОБ; |
|
|||||||
|
|
|
|
|
|
|||
Y – конечный продукт расширенной модели МОБ, |
|
|||||||
Тогда система (2.6) запишется |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
Х = АХ + |
Ф + Y . |
(2.22) |
||||
Дополним её системой балансов основных фондов, устанавливающей равенство ресурсов и потребностей по каждому виду основных фондов в
среднегодовом исчислении: |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Фk |
Фk |
fkj x j |
Rk , |
(2.23) |
||
где Фk – |
среднегодовой объём фондов kj-го вида на начало года; |
|
|||||||
|
|
|
|
|
|||||
|
Ф k |
– среднегодовой ввод фондов k-го вида; |
|
||||||
19

fkj – коэффициенты прямой фондоёмкости;
Rk – среднегодовое выбытие фондов k-го вида.
Переход от величины среднегодового ввода в действие основных фондов к абсолютному и обратно осуществляется с помощью коэффициентов равномерности ввода в действие основных фондов k :
|
|
|
|
|
|
. |
|
|
|
|
Фk λ |
k |
Ф |
k |
|
|
|
||
|
|
|
|
|
|
|
|
||
С учётом этого, уравнение (2.23) в матричном виде перепишется |
|
||||||||
|
|
|
|
|
|||||
Ф + |
Ф = FX + R , |
(2.24) |
|||||||
где – диагональная матрица коэффициентов равномерности ввода в действие основных фондов.
Система уравнений распределения продукции и баланс основных фондов (2.24) вместе образуют систему уравнений расширенной модели МОБ
(E |
A)X |
|
Ф |
Y |
||
|
|
|
|
|
|
|
F X |
Λ |
Ф |
Ф |
R . |
||
Решая её совместно, получим объёмы выпуска продукции Х и обеспечивающий
их прирост основных фондов |
Ф. |
2.5 Динамическая |
модель межотраслевых связей (траектория |
равновесного роста) |
|
До сих пор рассматриваемые нами модели описывали экономическую деятельность лишь в течение одного производственного периода.
Рассмотрим один из вариантов динамической межотраслевой модели, а именно, модель экономического роста, в которой проблема оптимизации в явном виде не ставится. В этой модели отражается взаимосвязь капитальных вложений текущего периода и прироста выпуска продукции в последующем периоде, причём предполагается, что темпы прироста производства всех благ
одинаковы и неизменны и равны q. |
|
|
Межотраслевую модель (2.7) можно записать в виде |
|
|
X(t) = A X(t) + Y(t) , |
(2.25) |
|
где t – момент времени. |
|
|
Вектор Y конечного спроса состоит из двух компонентов – вектора |
||
потребления С и вектора инвестиций |
Ф, т.е. |
|
Y(t) = C(t) + |
Ф(t) |
(2.26) |
20
