
- •Содержание
- •Если события А, В, С совместны, то
- •Формула полной вероятности имеет вид
- •ТЕМА 3. ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ
- •Пусть С – постоянная величина. Тогда
- •Для вычисления дисперсии используется формула
- •Дисперсия обладает свойствами
- •Если случайная величина распределена по закону Пуассона, то
- •Плотность нормального распределения имеет вид
- •Дисперсия нормального распределения
- •Правило трех сигм записывается в виде равенства
- •1. Ошибка указания времени часами со скачущей минутной стрелкой имеет равномерное распределение. Определить вероятность того, что при определении времени ошибка не будет превышать 20 секунд.
- •В предельной форме утверждения теоремы Бернулли имеют вид
- •На практике для вычисления дисперсии применяется формула
- •Легко установить, что
- •Вычислим размах товарооборота по формуле (9.14). Получим, что
- •ТЕМА 10. СТАТИСТИЧЕСКИЕ ОЦЕНКИ
- •ТЕМА 11. КОРРЕЛЯЦИЯ И РЕГРЕССИЯ
- •Непосредственно из этого определения следует, что
- •Найденные из систем (11.16) и (11.17) параметры подставляют, соответственно, в (11.14) и (11.15). В итоге получим искомое теоретическое уравнение регрессии Y на Х, предполагаемая кривая которого выравнивает эмпирическую кривую регрессии Y на Х.
- •Уравнение (11.11) очевидным образом преобразуется к виду
- •ТЕМА 12. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

56
М(Х) = |
a b |
; |
Д(Х) = |
(b a)2 |
. |
(7.3) |
|
2 |
12 |
||||||
|
|
|
|
|
Вероятность попадания этой случайной величины на отрезок [c,d] [a, b] находится по формуле
Р(с<Х<d) = |
d |
c |
. |
(7.4) |
|||
|
|
||||||
|
|
|
b |
a |
|
||
Дифференциальная функция |
показательного |
распределения |
|||||
выражается аналитически равенством |
|
|
|
||||
f(х) = |
0, |
если х |
0; |
(7.5) |
|||
e x , если х |
0. |
||||||
|
|
||||||
Положительная постоянная |
называется |
параметром |
показательного |
||||
распределения. Интегральная функция F(х) имеет вид |
|
||||||
F(х) = |
0, |
если х |
0; |
(7.6) |
|||
1 e |
x , если |
х 0. |
|||||
Числовые характеристики показательного распределения находятся по следующим формулам:
М(Х) = |
1 |
; |
Д(Х) = |
1 |
; |
(Х) = |
1 |
. |
(7.7) |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
Вероятность попадания на промежуток <а, b> непрерывной случайной величины, распределенной по показательному закону, находится по формуле
Р(с<Х<d) = е а- е b. |
(7.8) |
Плотность нормального распределения имеет вид
f(х) = |
1 |
|
e |
||
|
|
|
|||
|
|
|
|||
2 |
|||||
|
|
|
|||
( x a)2 |
|
|
|
|
2 |
2 |
, |
> 0. |
(7.9) |
|
|
|
|
|
Числа а и 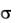 называются параметрами нормального распределения. При а=0 и =1 нормальное распределение называется нормированным. Функция нормированного распределения табулирована. Интегральная функция общего нормального распределения имеет вид
называются параметрами нормального распределения. При а=0 и =1 нормальное распределение называется нормированным. Функция нормированного распределения табулирована. Интегральная функция общего нормального распределения имеет вид
|
1 |
|
x |
|
(t a) 2 |
|
|
||
F(х) = |
|
e 2 |
2 dt . |
(7.10) |
|||||
|
|
||||||||
|
|
|
|
||||||
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
||
Математическое ожидание нормального распределения равно
параметру а: |
|
М(Х) = а. |
(7.11) |
Дисперсия нормального распределения |
|
Д(Х) = 2. |
(7.12) |
Следовательно, среднее квадратическое отклонение равно второму
параметру : |
|
(Х) = . |
(7.13) |

57
Вероятность того, что нормальная случайная величина Х примет значение, принадлежащее промежутку < , >, находится по формуле
Р( <Х< ) = Ф |
a |
Ф |
a |
, |
(7.14) |
|
|
где Ф(х) – функция Лапласа, для которой имеется таблица ее значений. Вероятность того, что отклонение такой случайной величины по абсолютной величине будет меньше заданного числа >0, находится из равенства
|
Р |
|
X |
a |
|
= 2Ф |
|
. |
(7.15) |
|
|
|
|
|
|||||||
|
|
|
||||||||
Правило трех сигм записывается в виде равенства |
|
|||||||||
|
|
|
= 2Ф (3) 0,9973. |
(7.16) |
||||||
Р |
X a |
|
3 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
Р е ш е н и е т и п о в ы х з а д а ч
Задача 1. Определить вероятность того, что случайная величина, равномерно распределенная на отрезке [2, 7], примет значение в промежутке [5, 6].
Решение. С помощью формулы (7.4) получаем
Р (5 Х 6) = |
6 |
5 |
= 0,2. |
|
7 |
2 |
|||
|
|
Задача 2. Троллейбусы некоторого городского маршрута идут с интервалом в 6 минут. Пассажир подходит к остановке в некоторый момент времени. Требуется: 1) определить плотность вероятности и функцию распределения случайной величины Х – времени, в течение которого пассажир будет ожидать троллейбус; 2) вычислить ее математическое ожидание и дисперсию; 3) найти вероятность появления пассажира на остановке не ранее, чем через две минуты после ухода предыдущего троллейбуса, но не позднее, чем за минуту до отхода следующего.
Решение. 1. Время, в течение которого пассажир будет ожидать троллейбус, представляет собой случайную величину, имеющую равномерное распределение. Следовательно, по формуле (7.1) определим плотность распределения случайной величины Х:
|
|
0 при х |
0, |
|
f(х) = |
1 |
|
при 0 |
х 6, |
6 |
|
|||
|
|
|
|
|
|
0 |
при х |
6. |
|
По формуле (7.2) получаем выражение для функции распределения:
|
0 |
при |
х |
0, |
|
F(х) = |
x |
при 0 |
|
х 6, |
|
6 |
|
|
|||
|
|
|
|
|
|
|
1 |
при |
х |
6. |
|

58
2. Для нахождения математического ожидания и дисперсии применим формулы (7.3). Получим следующие значения:
М(Х) = |
0 6 |
3 ; |
Д(Х) = |
(6 0)2 |
= 3. |
|
2 |
12 |
|||||
|
|
|
|
3. Если пассажир подойдет к остановке не ранее чем через две минуты после ухода предыдущего троллейбуса, но не позднее чем за минуту до отхода следующего, то он будет ожидать троллейбус не менее минуты и не более четырех минут. По формуле (7.4) определяем вероятность того, что случайная величина Х примет значение в промежутке [1, 4]:
Р (1 Х 4) = |
4 1 |
= |
1 |
. |
|
6 |
2 |
||||
|
|
|
Задача 3. Случайная величина подчинена показательному закону распределения с параметром . Найти вероятность того, что случайная величина примет значение меньшее ее математического ожидания.
Решение. Для показательного распределения, согласно (7.7), М(Х)= 1 .
Вероятность того, что случайная величина Х примет значение в интервале 0, 1 , определяем по формуле (7.8):
|
1 |
|
0 |
1 |
|
1 |
|
||
|
|
|
|
|
|
||||
Р (0 < Х < |
) = e |
-e = 1- |
0,6 321. |
||||||
|
|
e |
|||||||
|
|
|
|
|
|
|
|
||
Задача 4. Функция распределения случайного времени безотказной
t
работы радиоаппаратуры имеет вид: для t<0 F(t)=0 и для t 0 F(t) = 1-е T . Найти: 1) плотность вероятности f(t); 2) вероятность безотказной работы аппаратуры в течение времени Т.
Решение. 1. Для отыскания f(t) можно воспользоваться равенством
f(t)=F (t) или формулами (7.6) и (7.5) с |
= |
1 |
. Тогда |
||
T |
|||||
|
|
|
|
||
0 |
при t |
0, |
|||
f(t) = 1 е |
T |
при t 0. |
|||
|
t |
|
|
|
|
Т
2. Вероятность безотказной работы аппаратуры за время Т вычислим по формуле
Р (t T) = 1- Р (0 |
t < T). |
|
|
||||||
Значение Р (0 t < T) находим по формуле (7.8) |
|
|
|
||||||
1 |
0 |
1 |
T |
|
1 |
|
|||
Р (0 t < T) = e |
T |
e |
T |
1 |
. |
||||
|
|
|
|||||||
|
|
|
|
|
|
|
e |
||
Следовательно, Р (t T) = 1-(1-е -1) = е –1 |
0,367 879. |
||||||||
Задача 5. Найти плотность распределения нормально распределенной случайной величины, если известны ее числовые характеристики: М(Х) = 4, (Х)= 
 3 . Построить график этого распределения.
3 . Построить график этого распределения.

59
Решение. Согласно (7.11)-(7.13) и условию задачи имеем, что а=4, = 
 3 . Плотность вероятности нормально распределенной случайной
3 . Плотность вероятности нормально распределенной случайной
величины имеет вид (7.9). Подставляя данные значения а и |
|
в (7.9), |
||||||||||||||||
получим искомую плотность вероятности |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 |
|
|
( x 4) 2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
f(х)= |
|
e |
6 |
. |
|
|
|
|
|
|
|
|||
|
|
|
|
6 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Функция f(х) имеет максимум |
|
при х=4, |
равный f(4)= |
|
|
|
0,23 033. |
|||||||||||
|
|
|
|
|
||||||||||||||
|
6 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Абсциссы точек перегиба: х1= а- |
и х2=а+ . В данном случае |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
х1=4- 3 2,268 и х2=4+ 3 5,732; их ординаты: f(х1)=f(х2)= |
|
|
|
|
|
0,1 397. |
||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
||||||||||||||
6 e |
||||||||||||||||||
График функции симметричен относительно прямой х=4, ось абсцисс является асимптотой.
y
1 
 6
6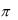
1

 6 e
6 e
|
|
|
|
|
4- 3 4 4+ 3 |
x |
|||
Задача 6. Рост взрослых мужчин является случайной величиной, которая распределена по нормальному закону. Пусть ее математическое ожидание равно 176 см, а дисперсия – 25. Найти плотность распределения

60
вероятностей и функцию распределения этой случайной величины. Вычислить вероятность того, что рост наугад выбранного мужчины будет находиться в пределах от 173 до 180 см.
Решение. По условию задачи а=176, = 
 25 =5. Поэтому согласно (7.9) плотность распределения вероятностей данной случайной величины такова:
25 =5. Поэтому согласно (7.9) плотность распределения вероятностей данной случайной величины такова:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
( x |
176) 2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(х) = |
|
|
|
|
|
e |
50 |
|
|
. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем функцию распределения по формуле (7.10): |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x |
|
|
|
|
(t |
176) 2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(х) = 5 |
|
|
|
|
|
|
e |
50 |
|
|
dt . |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
176 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Введем подстановку z= |
, тогда dt=5dz. При t |
|
|
- |
переменная z - , |
||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
при t=х переменная z= |
x |
176 |
. Получим |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x 176 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 176 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
z 2 |
|
|
|
|
|
|
0 |
|
|
z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
5 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
5 |
|
|
|
|
|
|
|
1 |
|
|
|
x 176 |
|
||||||||||||||||||||||
F(х)= |
|
|
|
|
|
e 2 |
dz |
|
|
e |
|
2 dz |
|
|
|
|
|
|
|
|
|
|
e 2 dz |
|
Ф |
|
. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
5 |
||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
0 |
|
z 2 |
|
|
|
|
|
|
|
|
z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Здесь учтено, что |
e |
2 dz |
|
e 2 dz |
|
|
|
|
|
|
|
(интеграл Пуассона). Вычислим |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
по формуле (7.14) вероятность того, что выбранный наугад мужчина будет иметь рост от 173 до 180 см:
Р(173<Х<180)=Ф |
180 |
176 |
-Ф |
173 176 |
= Ф(0,8) – Ф(-0,6) =Ф(0,8) +Ф(0,6). |
|
|
|
|
||||
5 |
5 |
|
|
|||
Из приложения 2 ([5]) находим Ф(0,8) |
|
0,2 881, Ф(0,6) 0,2 257. |
||||
Окончательно имеем: Р(173<Х<180) |
0,5 138. |
|||||
Задача 7. Завод изготовляет шарики для подшипников. Номинальный диаметр шариков d0=5 мм. Вследствие неточности изготовления шарика фактический его диаметр – случайная величина, описываемая нормальным законом распределения со средним значением d0 и средним квадратическим отклонением =0,05. При контроле бракуются все шарики, диаметр которых отличается от номинального больше чем на 0,1 мм. Определить, какой процент шариков будет отбраковываться.
Решение. Пусть Х – случайная величина, выражающая диаметр шарика. По условию задачи требуется определить в процентах Р X d0 0,1 .
Определим вероятность противоположного события, т.е. Р X d0 0,1 . Применяя формулу (7.15), получим
0,1
Р X 5 0,1 = 2Ф 0,05 = 2Ф(2).
По таблице (приложение 2 из [5]) находим Ф(2) 0,4 772. Тогда искомая вероятность равна
