
- •Содержание
- •Если события А, В, С совместны, то
- •Формула полной вероятности имеет вид
- •ТЕМА 3. ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ
- •Пусть С – постоянная величина. Тогда
- •Для вычисления дисперсии используется формула
- •Дисперсия обладает свойствами
- •Если случайная величина распределена по закону Пуассона, то
- •Плотность нормального распределения имеет вид
- •Дисперсия нормального распределения
- •Правило трех сигм записывается в виде равенства
- •1. Ошибка указания времени часами со скачущей минутной стрелкой имеет равномерное распределение. Определить вероятность того, что при определении времени ошибка не будет превышать 20 секунд.
- •В предельной форме утверждения теоремы Бернулли имеют вид
- •На практике для вычисления дисперсии применяется формула
- •Легко установить, что
- •Вычислим размах товарооборота по формуле (9.14). Получим, что
- •ТЕМА 10. СТАТИСТИЧЕСКИЕ ОЦЕНКИ
- •ТЕМА 11. КОРРЕЛЯЦИЯ И РЕГРЕССИЯ
- •Непосредственно из этого определения следует, что
- •Найденные из систем (11.16) и (11.17) параметры подставляют, соответственно, в (11.14) и (11.15). В итоге получим искомое теоретическое уравнение регрессии Y на Х, предполагаемая кривая которого выравнивает эмпирическую кривую регрессии Y на Х.
- •Уравнение (11.11) очевидным образом преобразуется к виду
- •ТЕМА 12. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

20
ТЕМА 3. ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ
Определение повторных независимых испытаний. Формула Бернулли и ее следствия. Наивероятнейшая частота появления события и ее
|
|
1 |
|
|
x 2 |
|
|
вычисление. Локальная теорема Муавра-Лапласа. Функция x |
|
|
e 2 |
и |
|||
|
|
|
|||||
|
|
|
|||||
2 |
|||||||
|
|
|
|
|
|
||
ее свойства. Формула Пуассона и ее приложения. Интегральная теорема Муавра-Лапласа. Функция Лапласа и ее свойства. Вероятности отклонений частоты от наивероятнейшей частоты и относительной частоты от вероятности появления события.
Л и т е р а т у р а
[2], гл.1, § 3, гл.5, § 3-5; [3], гл.4; [5], гл.5, § 1-4, гл.6, § 5,6; [6], гл.1; [7], гл.5, 6; [8], гл.2, § 1-3; [9], гл.2, § 1-5; [11], гл.28, § 189-195; [12], ч.2, гл.2, § 5-8; [13], гл.20, § 8; [15], гл.4, § 1-3.
О с н о в н ы е ф о р м у л ы и м е т о д и ч е с к и е у к а з а н и я
Если производится n повторных независимых опытов, в каждом из которых появляется либо событие А с вероятностью р, либо событие A с вероятностью q=1-р, то вероятность Рn(m) того, что событие А появится ровно m раз, выражается формулой Бернулли
Рn(m) = Cnm рm qn-m. |
(3.1) |
Вероятность того, что А появится хотя бы один раз при n повторных
независимых испытаниях, вычисляется по следующей формуле: |
|
|
Рn (m |
1) = 1 – qn . |
(3.2) |
Наивероятнейшая частота m0 |
удовлетворяет неравенствам |
|
np – q |
m0 np + p. |
(3.3) |
Если число np+p – целое, то наивероятнейшее число m0 имеет только одно значение. Этим значением будет целая часть числа np+р. Если np+p – число дробное, то m0 принимает два значения: m0=np-q=np+p-1 и m0=np+p. При достаточно большом числе проведенных испытаний m0 примерно равно np (m0 np).
При большом числе испытаний для вычисления Рn(m) применяются
следующие приближенные равенства: |
|
|
|
|
|
||||
Рn(m) |
|
1 |
|
|
m np |
, |
(3.4) |
||
|
|
|
|
|
|
|
|||
npq |
|
npq |
|||||||
|
|
|
|
|
|||||
m
Рn(m) |
|
e ( np). |
(3.5) |
m! |

21
В литературе обычно имеются таблицы значений функции
|
|
1 |
|
|
x 2 |
|
x |
|
|
e 2 |
|||
|
|
|
||||
|
|
|
||||
2 |
||||||
|
|
|
|
|
||
m
и выражения р(m, λ) = m! e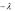 .
.
Вероятность того, что событие А наступит не менее k раз и не более r раз, находится по приближенной формуле
|
|
|
|
|
Рn (k |
m r) Ф |
r np |
- Ф |
k |
np |
|
, |
(3.6) |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
npq |
|
|
npq |
|
|||
|
|
1 |
|
x |
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
где Ф(х) = |
|
|
e 2 dt |
- функция Лапласа, для которой имеется таблица |
|||||||||||||
|
|
|
|
||||||||||||||
|
|
0 |
|||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
значений.
Формула (3.4) называется локальной теоремой Муавра-Лапласа, формула (3.6) – интегральной теоремой Муавра-Лапласа. Формулу (3.5) называют теоремой Пуассона.
Вероятности отклонений частоты m от наивероятнейшей частоты m0 и относительной частоты W от постоянной вероятности р события А при достаточно больших n вычисляются, соответственно, по следующим приближенным формулам:
|
|
|
|
|
Рn |
|
m |
np |
|
|
|
|
2 Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
(3.7) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
npq |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
Рn |
|
|
m |
p |
|
|
2 |
|
|
|
|
n |
|
|
|
|
|
, |
|
(3.8) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
npq |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где Ф(х) – функция Лапласа и |
- любое положительное число. |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При n |
величина 2Ф |
|
|
n |
|
|
|
|
2 Ф |
|
|
|
n |
|
|
стремится к единице. Тогда |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
pq |
|
|
|||||||||||||||||||||||
|
|
npq |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
событие |
|
m |
p |
|
практически достоверно. Если число |
достаточно мало, |
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
n |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то за |
гипотетическую |
вероятность р |
|
|
|
события А |
можно принять |
|||||||||||||||||||||||||||||
относительную |
частоту |
|
W(А) |
= |
|
|
m |
|
этого |
события. |
Величина |
, |
||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
n |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
определяемая равенством |
|
|
|
|
|
Рn |
|
|
m |
p |
|
|
|
|
|
|
|
, |
|
|
называется |
надежностью. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, надежность есть вероятность совпадения частоты W= mn и
вероятности р появления события в отдельном испытании с точностью до
: р= mn  .
.
При практическом применении теории вероятностей часто встречаются задачи на повторение опытов (испытаний). Многие же задачи моделируются как задачи на повторные испытания. Решаются они просто в

22
случае, когда опыты являются независимыми. В этом прежде всего и надо убедиться.
В каждом отдельном опыте появляется либо событие А, либо ему противоположное A (в конкретной задаче эти события надо сразу описать). Если вероятность события А во всех опытах постоянна (опыт производится в одинаковых условиях, Р(А)=р, Р( A )=q 1-р), то говорят, что имеет место схема Бернулли. Тогда Рn(m) вычисляется по формуле
(3.1).
Может быть и более общая схема: независимые опыты производятся в различных условиях (вероятность события А от опыта к опыту меняется). Имеется способ вычисления Рn(m) и в этой ситуации (см., например, [3] ).
Примерами независмых опытов являются: неоднократное бросание монеты (игральной кости), многократное извлечение карты из колоды (шара из урны, изделия из партии) при условии, что выбранный предмет возвращается.
Иногда допускают ошибку. В отборах без возвращения применяют биномиальное распределение (формулу Бернулли), на самом же деле надо применять гипергеометрическое распределение. Поясним это разбором задачи.
В урне находятся 5 белых и 10 черных шаров. Из урны наугад извлекли 3 шара. Какова вероятность того, что два из них окажутся белыми?
Решение (ошибочное). Обозначим через А событие, состоящее в том, что отдельно взятый шар будет белым. Тогда, согласно условию, за р
принимают число 155 : р= 13 , q= 23 . Далее, полагают n=3, m=2. Вероятность
искомого события (два белых шара при вынутых трех) вычисляют по формуле Бернулли:
Р (2) = C2 |
1 |
2 |
2 |
1 |
3 |
1 |
2 |
|
2 |
. |
||
|
|
|
|
|
|
|
|
|||||
3 |
3 |
3 |
|
3 |
|
9 |
3 |
9 |
|
|||
|
|
|
|
|
||||||||
Приведенное решение было бы верным, если бы опыты проводились в неизменных условиях. Для этого шары надо обратно возвращать в урну и перемешивать. По условию нашей задачи из урны вынули три шара (следовательно, они не возвращались). В этом случае уже нельзя говорить о неизменности условий всех трех опытов, так как после каждого извлечения состав шаров в урне будет меняться.
Для правильного решения применим классический способ подсчета
вероятностей. Число возможных |
исходов будет |
C3 |
, |
из них |
||||||
|
|
|
|
|
|
|
|
15 |
|
|
благоприятными для интересующего нас события будут |
C2 |
C1 |
исходов. |
|||||||
|
|
|
|
|
|
|
|
5 |
10 |
|
Тогда искомая вероятность Р= |
C 2 |
C1 |
5 10 |
10 |
. |
|
|
|
||
5 |
10 |
|
|
|
|
|
|
|
||
C3 |
455 |
91 |
|
|
|
|||||
|
|
|
|
|
||||||
|
|
15 |
|
|
|
|
|
|
|
|

23
Формула Бернулли (3.1) дает точное значение Рn(m), однако для больших значений n и m появляются вычислительные трудности, прежде
всего из-за выражения для Cm . |
Поясним это примером. |
Пусть n=1000, |
||||
|
|
n |
|
|
|
|
m=25, р=0,03. Тогда |
согласно |
(3.1) |
надо |
вычислять выражение |
||
C25 |
(0,03)25(0,97)975. |
|
|
|
|
|
1000 |
|
|
|
|
|
|
Поэтому возникает |
необходимость в |
более |
простых |
формулах для |
||
Рn(m). Таковыми являются формулы (но уже приближенные) (3.4) и (3.5). Формула (3.4) дает тем более близкие к точному значению Рn(m)
результаты, чем больше значение 

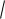 npq . При этом здесь сказывается не только значение n, но и значение pq. Обычно формулой (3.4) пользуются, когда npq 20. Из этого ограничения видно, что чем ближе одно из чисел p или q к нулю (другое число будет близко к единице), тем большим надо
npq . При этом здесь сказывается не только значение n, но и значение pq. Обычно формулой (3.4) пользуются, когда npq 20. Из этого ограничения видно, что чем ближе одно из чисел p или q к нулю (другое число будет близко к единице), тем большим надо
брать n. Погрешность этой формулы порядка 1 .
 n
n
Найдем наибольшее значение выражения pq р(1-р). Рассмотрим
функцию f(р)=р(1-р) р-р2, |
0 р |
1. Очевидно, что она достигает своего |
|||
наибольшего значения |
1 |
|
при р= |
1 |
. Следовательно, при одних и тех же |
4 |
|
2 |
|||
|
|
|
|
||
значениях n формула (3.4) дает тем лучшее приближение к значению Рn(m) из формулы Бернулли, чем ближе pq к своему наибольшему значению 0,25, т.е. чем ближе р (отсюда и q) к 0,5.
В случае, если вероятность р близка к нулю и число n мало, формула (3.4) дает заметные отклонения от формулы Бернулли.
Асимптотическая формула (3.5) применяется для редких событий (со значениями р, близкими к нулю). Приближение тем лучше, чем больше n и меньше p. Обычно формулой (3.5) пользуются при условии =np 10. Погрешность формулы (3.5)  np2.
np2.
Задачи с редкими событиями встречаются на практике в лотереях, страховании, при проверке качества изделий с низким процентом брака, в медицине (рождение близнецов, заболевание редкой инфекционной болезнью) и т.п.
Если р близко к единице (например, р 0,97), то q близко к нулю (q 0,03). Тогда формулу Пуассона (3.5) можно применить для вычисления вероятности того, что A произойдет n-m раз. Надо в (3.5) положить =nq, а вместо m написать n-m. Найденная вероятность даст приближенное значение вероятности того, что А произойдет ровно m раз.
Как уже отмечалось, для функций (х) и р(m, |
) имеются таблицы. Так |
|
как (х) четна ( |
(-х)= (х)), то ее таблицы составлены для х 0. При х>4 |
|
можно полагать |
(х) 0, так как (3,99) 0,0001 и |
(х) монотонно убывает |
при х>0. Если в таблице значений нет нужного аргумента, то можно провести либо округление этого аргумента до ближайшего, либо для
24
нахождения значения функции воспользоваться методом (линейной)
интерполяции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Поясним метод линейного интерполирования для нашей ситуации. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Аргумент x , |
которого нет в таблице, будет заключен между некоторыми |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
двумя аргументами х1 |
и х2, имеющимися |
в таблице (х1 < |
|
x < х2). |
||||||||||||||||||
Соответствующие аргументам х1 и х2 |
значения y1 |
и y2 нашей функции |
||||||||||||||||||||
будут даны |
в таблице: |
(х1) y1, |
(х2) y2. |
Тогда |
запишем |
уравнение |
||||||||||||||||
прямой, |
проходящей через точки |
(х1, y1) |
|
и (х2, y2). |
Оно имеет вид |
|||||||||||||||||
y-y = |
y2 |
y1 |
(x |
x ) ; ограничение х |
1 |
х |
2 |
выполняется автоматически, т.к. |
||||||||||||||
|
|
|||||||||||||||||||||
|
1 |
|
x2 |
x1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
х |
<х . Получилась линейная функция y= |
y2 |
y1 |
x y |
x |
y2 |
y1 |
|
. Значение |
|||||||||||||
|
|
|
|
|
||||||||||||||||||
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
x |
x |
1 |
1 |
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
2 |
1 |
|
|
|
|
этой линейной функции в точке x и принимают за приближенное значение неизвестного ( x ).
m
В ряде учебников имеются таблицы значений функции р(m, )= m ! e
для некоторых m и  (см., например, [8], [11] ). Иногда приводят (см.[3] ) только значения e x (одного множителя нашей функции). Значения второго
(см., например, [8], [11] ). Иногда приводят (см.[3] ) только значения e x (одного множителя нашей функции). Значения второго
|
xm |
|
множителя |
|
при небольших значениях m легко вычислить. |
|
||
|
m ! |
|
Если число n независимых испытаний мало и надо вычислить вероятность появления события А от k до r раз, то надо применить
r |
|
следующую формулу: Рn(k m r) = |
Рn(m). В этой ситуации k и r не |
m |
k |
могут быть большими (мало n) и все Рn(m) можно вычислить по формуле Бернулли. Приведенная формула есть следствие теоремы о вероятности суммы попарно несовместных событий.
Эту последнюю формулу можно применять и при достаточно большом числе испытаний, если в сумме справа число слагаемых невелико (мало число r-k). При этом для вычисления Рn(m) при малых значениях р (р 0,03) надо применять приближенную формулу (3.5), а в остальных случаях – (3.4).
r |
|
Если же число n велико и число слагаемых в сумме |
Рn(m) велико, |
m |
k |
то применяется приближенная формула Муавра-Лапласа (3.6). Условием ее применения является неравенство npq 20.
В этой формуле участвует функция Лапласа Ф(х), называемая еще интегралом вероятностей. Значения этой функции приводятся почти в каждом из рекомендуемых учебников. Только надо помнить, что в ряде учебников (см., например, [7], [8], [11] ) эти значения удвоены. Тогда в (3.6) надо подставлять значения в два раза меньшие (можно также, не

25
уменьшая этих значений, ввести справа в (3.6) множитель 12 , относящийся
к обоим слагаемым).
Таблицы Ф(х) приведены для х 0. Для отрицательных аргументов
значения |
этой |
функции |
находятся на |
основании ее свойства, что |
||||
Ф(-х) = -Ф(х) . Например, |
Ф(-2) = -Ф(2) |
-0,4 772 (см. [5], приложение 2). |
||||||
Далее, для х>5 |
приближенно полагают Ф(х) |
1 |
, так как Ф(5) 0,499 997 и |
|||||
|
||||||||
|
|
|
|
|
|
2 |
|
|
Ф(х) |
1 |
|
при х |
+ . |
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Сделаем некоторые пояснения по поводу формулы (3.8). Прежде всего она имеет теоретическое значение. Из нее следует так называемый закон больших чисел Бернулли, который будет рассмотрен в дальнейшем. Она объясняет, что статистическое определение вероятности события введено разумно.
Эта формула имеет значительные практические приложения. Зная р, n и , из (3.8) находим надежность . Если известны р, n и , то можно найти
точность . Наконец, что очень важно на практике, можно по р, заданным  и
и  оценить число n (число испытаний, необходимых для какого-нибудь
оценить число n (число испытаний, необходимых для какого-нибудь
контроля). Более того, можно оценить n только при известных |
и (р- |
|||||||||||||||
неизвестно). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Надежность приближенно получается из равенства (3.8): |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2Ф |
|
|
|
|
|
n |
. |
(3.9) |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
pq |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначим через t величину |
|
n |
: |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
pq |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
n |
|
|
|
|||||
|
|
t = |
|
|
|
|
. |
|
|
(3.10) |
||||||
|
|
|
|
pq |
|
|
||||||||||
Решая уравнение (3.9) ( |
= |
2Ф( t |
)), по таблице значений функции |
|||||||||||||
Лапласа Ф(х) найдем аргумент t |
, соответствующий данной надежности . |
|||||||||||||||
Из (3.10) находится точность |
при известных р, n и : |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
= t |
|
|
pq |
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|||||
Тогда с надежностью  определяются границы, в которых заключены частость и частота события в серии из n испытаний:
определяются границы, в которых заключены частость и частота события в серии из n испытаний:
m |
p |
, |
m np n . |
|
|
||||
n |
||||
|
|
|
Из (3.10) получается и формула для определения необходимого числа n испытаний при известных р, , :

26
t 2
n pq .
2
Из последнего равенства при неизвестном р в силу оценки pq=p(1-p) 14
t 2
получаем n n0 , т.е. достаточно провести n0 испытаний для
4 2
определения неизвестной вероятности р появления события с заданной точностью и надежностью.
Р е ш е н и е т и п о в ы х з а д а ч
Задача 1. Вероятность того, что в данный день торговая база уложится в норму транспортных расходов, равна ¾. Определить веротяность того, что торговая база уложится в норму транспортных расходов только в два дня при шестидневной рабочей неделе.
Решение. Обозначим через А событие, что в любой день рабочей недели торговая база уложится в норму своих транспортных расходов, тогда A - база не уложится в эту норму. Вероятности этих событий постоянны. Очевидно, что эту задачу можно моделировать как задачу на повторные
|
|
|
|
|
||||
независимые |
испытания: n=6, m=2, р=Р(А)=3/4 |
(q=Р( A )=1/4). |
||||||
Следовательно, |
по формуле Бернулли (3.1) искомая |
вероятность |
||||||
Р (2)= C2 |
3 |
2 |
1 |
4 |
|
|
|
|
|
|
|
0,033. |
|
|
|
||
|
|
|
|
|
|
|||
6 |
6 |
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||
Задача 2. В магазин завезли 500 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,002. Найти вероятность того, что магазин получит три разбитых бутылки.
Решение. Испытания, рассматриваемые в задаче, удовлетворяют схеме Бернулли. По условию задачи n=500, m=3, р=0,002. Так как n достаточно велико, а р=0,002 сравнительно мало, то для вычисления Р500(3) можно воспользоваться формулой Пуассона (3.5). Так как =np=1, то
Р500(3) |
e |
1 |
0,0 613. |
|
|
|
|||
3 ! |
||||
|
|
|||
Задача 3. По статистическим данным среди специалистов с высшим и средним специальным образованием женщины составляют 60%. На предприятии 240 таких работников. Определить наивероятнейшее число специалистов-мужчин, имеющих среднее специальное и высшее образование, и соответствующую ему вероятность.
Решение. Так как надо определить наивероятнейшее число специалистов-мужчин, то через А обозначим событие, состоящее в том, что выбранный специалист с высшим или средним специальным образованием – мужчина. Тогда событие A означает, что выбранная

27
женщина имеет высшее или среднее специальное образование. По
|
|
|
|
||
условию задачи n=240, p=Р(А)=0,4 (тогда |
q=Р( A )=0,6). Следовательно, |
||||
240 0,4 - 0,6 |
m0 240 |
0,4+0,4, 95,4 m0 |
96,4. Так как m0 – целое число, |
||
то наиболее вероятно, |
что 96 мужчин будут иметь высшее или среднее |
||||
специальное |
образование. Для приближенного нахождения Р240(96) |
||||
применим |
локальную теорему |
Лапласа |
(3.4). Вначале вычислим |
||||||||||||
|
m np |
96 |
240 |
0,4 |
|
= 0. По таблице (см. [5], приложение 1) найдем |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
npq |
240 0,6 |
0,4 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
(0) 0,3 989. Следовательно, искомая вероятность |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
Р240(96) |
|
1 |
|
0,3989 |
0,0 526. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
57,6 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 4. |
Вероятность попадания в цель при отдельном выстреле равна |
||||||||||||
0,001. Найти вероятность попадания в цель хотя бы один раз, если произведено 5000 выстрелов.
Решение. По условию задачи n=5 000, р=0,001, m 1. Надо найти Р5000 (m 1). Можно применить формулу (3.2), где q=1-0,001=0,999. Чтобы не вычислять значение qn=(0,999)5 000, нужно по формуле (3.5) для редких
событий вычислить Р5 000(0). Так как =np=5 000 0,001=5, то Р5 000(0)=е-5.
Тогда искомая вероятность Р5 000(m 1)=1-Р5 000(0) =1-е-5 1-0,0 067 =0,9 933.
Задача 5. На автоматическом станке с программным управлением изготовлены 24 изделия. Вероятность того, что изделие будет высшего сорта, равна 0,6. Найти наивероятнейшее число изделий высшего сорта, произведенных на данном станке.
Решение. Проводятся 24 повторных независимых испытания с двумя исходами в каждом (деталь высшего сорта и деталь не высшего сорта). По условию р=0,6, q=0,4, n=24. Наивероятнейшее число изделий высшего
сорта находим из неравенств (3.3): 24 0,6 - 0,4 m0 24 0,6 + |
0,6 или |
14 m0 15. Получили два наивероятнейших числа, т.е. m0=14 |
и m0=15. |
Задача 6. По результатам проверки качества отобранного для посева зерна кукурузы всхожесть зерен составила 80%. Определить вероятность того, что среди отобранных и высаженных 400 зерен прорастет от 270 до
330 штук.
Решение. По условию задачи n=400, k=270, r=330. Для вычисления
Р400(270 |
m |
|
330) можно использовать формулу (3.6). Вычислим |
||||||||||||||||||
аргументы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
np |
270 |
400 |
0,8 |
6,25; |
|
r np |
330 |
400 |
0,8 |
1,25. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
npq |
400 |
0,8 |
0,2 |
|
|
|
npq |
400 |
0,8 |
0,2 |
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||||
По таблице Ф(х) найдем Ф(1,25) |
0,3 944. Так как Ф(х) нечетна, то |
||||||||||||||||||||
Ф(-6,25) = -Ф(6,25). Учитывая, что Ф(х) 0,5 для х>5, получим Ф(6,25) 0,5.
Следовательно, Р400 (270 m |
330) 0,3 944 + 0,5 = 0,8 944. |
|
Задача 7. |
В автобусном парке имеется 80 машин. Вероятность выхода |
|
автобуса на |
линию равна |
0,9. Для обеспечения нормальной работы |

28
маршрутов необходимо иметь на линиях не менее 70 машин. Определить вероятность нормального функционирования автобусных маршрутов.
Решение. Для нахождения вероятности того, что из имеющихся в наличии в автобусном парке 80 машин на маршруты выйдут не менее 70, воспользуемся формулой (3.6). По условию n=80, р=0,9, q=0,1. Далее, так как m 70, то k=70, r=80. Вычислим аргументы:
|
k np |
70 |
80 |
0,9 |
|
0,75; |
r |
np |
80 |
80 |
0,9 |
|
2,98. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
npq |
80 |
0,9 |
0,1 |
|
npq |
80 |
0,9 |
0,1 |
||||||||||
|
|
|
|
|
||||||||||||||||
Учитывая, что функция Лапласа нечетна, получим |
|
|
|
|
||||||||||||||||
Р80 (70 |
m |
80) |
|
Ф(2,98) – Ф(-0,75) = Ф(2,98) + Ф(0,75). |
||||||||||||||||
По таблице (см. [5], приложение 2) найдем Ф(2,98) |
0,4 986, |
|||||||||||||||||||
Ф(0,75) 0,2 734.Искомая вероятность Р80(70 |
m |
80) 0,4 986+0,2 734=0,772. |
||||||||||||||||||
Задача 8. Школа принимает в первые классы 200 детей. Определить вероятность того, что число девочек будет по абсолютной величине отличаться от наивероятнейшего их числа не более чем на 10, если вероятность рождения мальчика равна 0,515.
Решение. Условие задачи позволяет применить приближенное равенство (3.7). В нашем случае число независимых испытаний n=200, вероятность наступления события в отдельном испытании р=0,485 (q=1-р=1-0,485=0,515), =10. Подставляя данные задачи в (3.7), получим
Р200( |m-97| 10) 2Ф |
|
|
10 |
|
|
2Ф(1,41). |
|
|
|
|
|
||
|
|
|
|
|
||
|
0,485 |
0,515 |
||||
200 |
|
|
||||
По таблице (см. [5], приложение 2) найдем Ф(1,41) 0,4 207. Следовательно, 2Ф(1,41) 0,8 414. Таким образом, с вероятностью 0,8 414 можно ожидать, что число девочек, среди принятых в первые классы 200 детей, будет по абсолютной величине отличаться от наиболее вероятного их числа 97 не более чем на 10 человек.
Задача 9. При установившемся технологическом процессе вероятность изготовления бракованного шарика для шарикоподшипника равна 0,02. Определить вероятность того, что доля бракованных шариков среди 800 изготовленных будет отличаться от вероятности изготовления бракованного шарика не более чем на 0,01 в ту или другую сторону.
Решение. По условию n=800, р=0,02, q=0,98, =0,01. Воспользуемся
формулой (3.8). Имеем Р |
m |
0,02 |
0,01 |
2Ф 0,01 |
|
800 |
|
2Ф(0,64). |
|
|
|
||||||
800 |
0,02 0,98 |
По таблице (см. [5], приложение 2) найдем Ф(0,64) 0,2 389. Итак, искомая вероятность приближенно равна 0,4 778.
Задача 10. На керамическом заводе 90% тарелок выпускается продукцией первого сорта. Какое предельное отклонение (по абсолютной величине) доли первосортных тарелок от вероятности изготовления их

29
можно гарантировать с вероятностью 0,9 854 при проверке ОТК завода
партии из 560 изделий? |
|
|
|
|
|
|
|
|
|||||||
|
Решение. |
Согласно |
|
|
условию |
n=560, |
р=0,9, |
q=0,1, |
|||||||
Р |
|
m |
0,9 |
|
0,9854. Требуется найти |
. Воспользуемся формулой (3.8). |
|||||||||
|
|
||||||||||||||
|
|
|
|||||||||||||
|
560 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В |
силу условия |
2Ф |
560 |
|
0,9854 |
или Ф(78,881 |
) |
0,4 |
927. По |
||||||
|
|
|
|||||||||||||
0,9 |
0,1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
таблице (см.[5], приложение 2) значению 0,4 927 функции Ф(х) отвечает аргумент х=2,44. Таким образом, для отыскания  получаем уравнение 78,881 =2,44. Отсюда искомое отклонение =0,031.
получаем уравнение 78,881 =2,44. Отсюда искомое отклонение =0,031.
Задача 11. Всхожесть семян подсолнечника характеризуется вероятностью р=0,85. Сколько семян подсолнечника нужно посеять для контроля всхожести, чтобы с точностью в 1% гарантирвоать, что 96% из них прорастут?
m
Решение. По условию р=0,85, q=0,15, =0,01, Р 0,85 0,01 0,96. Из
n
|
|
n |
|
|
|
|
формулы (3.8) следует, что 2Ф 0,01 |
|
0,96 или Ф(0,028 n )=0,48. |
||||
|
|
|||||
0,85 0,15 |
||||||
По таблице (см.[5], приложение 2) значению 0,48 функции Ф(х) отвечает аргумент х 2,06. Отсюда 0,028 
 n 2,06; следовательно, n=5413. Это число определяет объем работы контролирующей лаборатории.
n 2,06; следовательно, n=5413. Это число определяет объем работы контролирующей лаборатории.
За д а ч и
1.В хлопке содержится 20% коротких волокон. Определить вероятность того, что среди пяти отобранных наудачу волокон окажется три длинных.
2.Письменная экзаменационная работа по математике состоит из пяти задач, причем за решение любой задачи ставится 1 балл. Вероятность решения любой задачи для некоторого абитуриента равна 0,8. Определить вероятность того, что этот абитуриент получит за экзамен не менее 4 баллов.
3.По данным технического контроля в среднем 15% изготовляемых на заводе часов нуждаются в дополнительной регулировке. Найти
30
вероятность того, что из 300 изготовленных за смену часов 240 не будут нуждаться в дополнительной регулировке.
4.В стаде, содержащем 2 000 овец, проводятся прививки против заболеваний животных. Какова вероятность того, что при вакцинации заболеют три овцы, если вероятность заболевания каждого животного при вакцинации равна 0,001?
5.Счетчик Гейгера регистрирует частицы, вылетающие из некоторого радиоактивного источника, с вероятностью 0,0 002. Какова вероятность того, что счетчик зарегистрировал 4 частицы, если за время наблюдения из источника вылетело 15 000 частиц?
6.Вероятность того, что консервная банка будет недостаточно герметизирована, равна 0,002. Среди скольких банок, отобранных случайным образом, можно с вероятностью 0,9 512 ожидать отсутствие бракованных?
7.Вероятность того, что на странице книги могут оказаться опечатки, равна 0,015. Определить вероятность того, что с опечатками окажется не более трех страниц книги, содержащей 620 страниц.
8.Радиолокационная станция за один цикл обзора обнаруживает крылатую ракету с вероятностью 0,25. Сколько потребуется циклов обзора для того, чтобы ракета была обнаружена с вероятностью не меньшей, чем 0,98?
9.На первый курс института поступило 480 человек. Найти наивероятнейшее число студентов первого курса, проживавших до поступления в институт в сельской местности, и соответствующую
вероятность, если численность городского населения составила в этом году 66%.
10.Оптовая база снабжает 24 магазина, от каждого из которых может поступить заявка на очередной день с вероятностью 0,6 независимо от заявок других магазинов. Найти наивероятнейшее число заявок в день и вероятность получения этого числа заявок.
11.Опытным путем установлено, что 80% растений рассады помидоров приживаются. Сколько надо посадить кустов помидоров, чтобы наивероятнейшее число неприжившихся было равно 30?
12.Установлено, что в среднем 70% посетителей уходят из магазина с покупками. Чему равна вероятность того, что из 250 посетителей магазина покупки сделают не менее 160 и не более 200 человек?
13.При изготовлении на термопластавтомате цветной облицовочной плитки 80% изделий выходит высшим сортом. Определить вероятность того, что число плиток высшего сорта среди 2 000 изготовленных будет по абсолютной величине отличаться от наиболее вероятного числа их не более чем на 30.
14.Статистическая вероятность наступления несчастного случая в течение года для моряка торгового флота равна 0,0 004. В пароходстве работает
31
5 000 моряков. Определить: 1) наиболее вероятное число несчастных случаев среди моряков этого пароходства и соответствующую вероятность; 2) вероятность того, что число пострадавших в течение года моряков отклонится от наивероятнейшего числа в ту или другую сторону не более чем на 2 человека.
15.Известно, что 60% всего числа изготовляемых заводом телефонных аппаратов выпускаются первым сортом. Какова вероятность того, что среди 400 проверенных приемщиком аппаратов доля первого сорта будет отличаться от вероятности изготовления аппарата первого сорта по абсолютной величине не более чем на 0,01?
16.На склад поступают детали, проверенные ОТК или изготовленные рабочими, имеющими личное клеймо. Вероятность того, что деталь помечена личным клеймом, равна 0,2. Определить, сколько нужно взять деталей, чтобы с вероятностью, равной 0,9 892, можно было утверждать, что доля деталей с личным клеймом среди них будет отличаться от вероятности изготовления детали рабочим с личным клеймом по абсолютной величине не более чем на 0,02?
17.К распределительному щиту подключено 600 лампочек, вероятность включения каждой из которых за время Т равна 0,8. Найти границу абсолютной величины отклонения частости включенных лампочек от вероятности включения лампочки, если эта граница должна быть гарантирована с вероятностью 0,9 826.
18.Для определения нормы высева требуется определить всхожесть семян с точностью до 2% и надежностью 98%. Сколько семян надо посеять?

32
ТЕМА 4. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ЗАКОНЫ ИХ РАСПРЕДЕЛЕНИЯ
Понятие случайной величины. Дискретные и непрерывные случайные величины. Примеры случайных величин. Закон распределения случайной величины. Ряд распределения дискретной случайной величины. Многоугольник распределения (полигон). Функция F(х) распределения случайной величины (интегральная функция) и ее свойства. Вид функции F(х) для дискретной случайной величины. Графики функции F(х) для дискретных и непрерывных случайных величин. Плотность вероятности (дифференциальная функция f(х)) и ее свойства. Вероятностный смысл дифференциальной функции. Связь между дифференциальной и интегральной функциями. Вероятность попадания непрерывной случайной величины в заданный промежуток.
Л и т е р а т у р а
[2], гл. 3, § 1, 2; [3], гл.5, 5.1-5.4; [5], гл.6, § 1-3, гл.10, § 1-3, гл.11, § 1-5; [6], гл.4, § 18,19; [7], гл.7, § 18,19, гл.12, § 29, 30; [8], гл.3, § 1, гл.4, § 1-3; [9], гл.2, § 1, гл.3, § 1-4; [10], гл.3, § 1, 2; [11], гл.29, § 196-198; [12], гл.3, § 9; [13], гл.20, § 7, § 12, 13; [14], § 1; [15], гл.5, § 1-3; [16], гл.2, 2.1, 2.2.1- 2.2.3, 2.6.1.
О с н о в н ы е п о л о ж е н и я и ф о р м у л ы
Рассмотрим событие Х< х, состоящее в том, что случайная величина Х примет какое-нибудь значение, меньше произвольного числа х. Функция
F(х), определенная равенством |
|
F(х) = Р (Х< х), |
(4.1) |
называется функцией распределения вероятностей случайной величины Х. Она обладает следующими свойствами:
|
1) |
0 |
F(х) |
1 |
|
|
(4.2) |
2) |
F(х2) |
F(х1) , |
если |
х2 |
> х1 ; |
(4.3) |
|
3) |
F(- ) = |
lim |
F(х) = 0, |
F(+ |
) = lim F x 1. |
(4.4) |
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
Для дискретной случайной величины (хi, рi) функция F(х) имеет вид |
|||||||
F(х) |
Р (Х < х) = |
pi , |
рi = P(Х=хi). |
(4.5) |
|||
|
|
i:xi |
x |
|
|
|
|
Так, для дискретной случайной величины с конечным множеством значений (i=1, …, n) F(х) имеет следующий вид:

|
33 |
|
|
|
0, |
если |
х |
х1; |
|
р1, |
если |
х1 |
х |
х2 ; |
р1 р2 , |
если |
х2 |
х |
х3; |
F(х) = |
|
|
|
(4.6) |
р1 ... |
рn 1, если хn 1 |
х |
хn ; |
|
1, |
если |
х |
хn . |
|
Для непрерывной случайной величины плотность распределения вероятностей f(х) в точке х определяется равенством
F(х) = lim |
P x X x x |
, |
(4.7) |
|
x |
||||
x 0 |
|
|
||
|
|
|
где х < Х < х+ х – событие, состоящее в том, что случайная величина примет значение, принадлежащее интервалу (х, х+ х) длины х. Так как Р(х < Х < х+ х) = F(х+ х) – F(х), то в точках существования произвольной функции F(х) имеет место равенство
f(х) = F’(х). (4.8)
Поэтому плотность часто называют дифференциальной функцией. Плотность распределения вероятностей обладает следующими
свойствами:
1)f(х)  0,
0,
( |
) |
|
2) |
f(х) dx = 1. |
(4.9) |
( )
Если плотность f(х) интегрируема, то можно найти функцию распределения F(х) по формуле
F(х) = |
x f t dt . |
(4.10) |
Вот почему функцию распределения часто называют интегральной функцией.
Если известна функция F(х), то вероятность попадания случайной величины на полуотрезок [а, b) находится по формуле
Р(а Х < b) = F(b) – F(а). (4.11)
Если известна плотность f(х) и она интегрируема на промежутке <a, b> (интервале, отрезке, любом полуотрезке), то
Р(а<Х<b) = b f (x) dx . |
(4.12) |
a |
|
Р е ш е н и е т и п о в ы х з а д а ч
Задача 1. В группе 25 студентов. По результатам экзаменационной сессии 18 студентов получают стипендию, причем 6 из них – повышенную. Построить ряд распределения и полигон величины стипендии для наудачу

34
выбранного студента этой группы, если размер обычной стипендии составляет 200 рублей, а повышенной – 250 рублей.
Решение. Случайная величина Х (величина стипендии) может принимать следующие значения: х1=0, х2=200, х3=250. Вероятности этих возможных значений соответственно равны: р1=7/25, р2=12/25, р3=6/25. Поэтому закон (ряд) распределения случайной величины Х имеет вид
Х 0 |
200 250 |
Р7/25 12/25 6/25
Полигон построить самостоятельно.
Задача 2. Составить функцию распределения и построить ее график для дискретной случайной величины Х, заданной законом распределения
|
|
|
Х |
1 |
|
|
3 |
4 |
|
|
7 |
|
|
|
||
|
|
|
Р |
0,2 |
|
0,1 |
0,4 |
|
|
0,3 |
|
|
|
|||
Решение. Составим функцию распределения |
F(х). Если х |
1, |
то |
|||||||||||||
F(х)=Р(Х<х)=0. Если 1< х |
3, |
то F(х)=Р(Х<х)= |
Р(Х=хi)=Р(Х=1)=0,2. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xi |
x |
|
|
|
Если |
3 < х |
4, то F(х)=Р(Х<х)= |
Р(Х=хi)=Р(Х=1)+Р(Х=3)=0,2+0,1=0,3. |
|||||||||||||
|
|
|
|
|
|
|
xi x |
|
|
|
|
|
|
|
|
|
Если |
4< х |
7, то |
F(х)=Р(Х=1)+Р(Х=3)+Р(Х=4)=0,7. Если |
х>7, |
то |
|||||||||||
F(х)=Р(Х=1)+Р(Х=3)+Р(Х=4)+Р(Х=7)=1.Следовательно, F(х) имеет вид |
|
|||||||||||||||
|
|
|
|
|
|
|
0, |
если |
х |
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2, |
если |
1 |
х |
3; |
|
|
|
|
|
|
|
|
|
F(х) |
= |
|
0,3, |
если |
3 |
х |
4; |
|
|
|
|
|
|
|
|
|
|
|
|
0,7, |
если |
4 |
х |
7; |
|
|
|
|
|
|
|
|
|
|
|
|
1, |
если |
х |
7. |
|
|
|
|
|
|
Составленную функцию распределения изобразим графически: y
х
Величины скачков в точках разрыва х=1, х=3, х=4, х=7 как раз равны вероятностям, что случайная величина Х примет эти значения.
Задача 3. Функция распределения непрерывной величины Х задана выражением

|
|
|
|
35 |
|
|
|
|
|
|
|
|
|
0 |
при |
х |
0, |
|
|
|
|
|
1 |
х |
2 |
при 0 |
х |
2, |
|
F(х) = |
|
|
6 |
|
|||||
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
х |
2 |
|
2х |
2 |
при |
2 |
х 3, |
|
|
3 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
при |
х |
3. |
|
|
Построить график этой функции. Найти вероятность попадания случайной величины на интервал (1; 2,5).
Решение. График функции изображен ниже на рисунке. y
0 |
х |
При 0 < х  2 графиком функции является часть параболы. Ветви параболы направлены вверх, а вершина находится в начале координат. При 2 < х
2 графиком функции является часть параболы. Ветви параболы направлены вверх, а вершина находится в начале координат. При 2 < х  3 график функции представляет собой часть параболы, вершина которой находится в точке (3; 1), а ветви направлены вниз. Для х 0 и х>3 графиком функции F(х) являются прямые y=0 и y=1.
3 график функции представляет собой часть параболы, вершина которой находится в точке (3; 1), а ветви направлены вниз. Для х 0 и х>3 графиком функции F(х) являются прямые y=0 и y=1.
По формуле (4.11) находим, что
Р(1<Х<2,5) = F(2,5) – F(1) = |
|
25 |
5 |
2 |
|
1 |
11 |
1 |
|
3 |
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
12 |
|
6 |
12 |
|
6 |
4 |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
Задача 4. Функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
при |
х |
0, |
|
|
|
|
|
|
|
|
|
|
|
||
f(х) = |
А |
при |
0 |
|
х |
|
, |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
cos2 х |
4 |
|
|
|
|
|
|
|
|
|||||||||
|
0 |
|
при |
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
служит плотностью вероятностей случайной величины Х. Найти коэффициент А. Вычислить вероятность того, что случайная величина Х
примет какое-нибудь значение из отрезка 0, 6 .
Решение. Используя равенство 2) из (4.9), получим
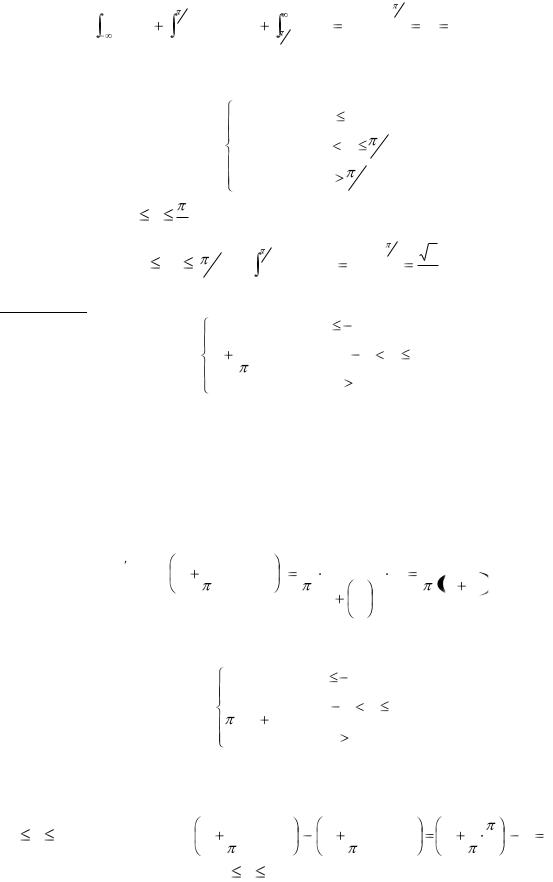
36
0 |
|
4 |
A |
|
|
|
4 |
|
0 dx |
|
|
dx |
|
0 dx A tg x |
A 1. |
|
0 |
cos2 x |
4 |
||||
|
|
|
|
|
|
|
0 |
Следовательно,
|
|
|
0 |
при |
х |
0, |
|
|
f(х) = |
1 |
|
|
при |
0 |
х |
4 , |
|
|
|
|
|
|||||
cos |
2 |
х |
||||||
|
|
|
|
|
|
|||
|
|
0 |
|
при |
х |
|
4. |
|
|
|
|
|
|
|
|
|
|
Для вычисления Р(0 Х 6 ) применим формулу (4.12). Получим
|
6 |
1 |
|
6 |
Р (0 Х |
6 ) = 0 |
|
|
|
|
dx tg x |
|
||
cos2 x |
0 |
|||
|
|
|
|
33 .
Задача 5. Дана функция распределения F(х) случайной величины Х:
|
|
0 |
при |
х |
2, |
||||
F(х) = |
1 |
|
2 |
arc tg |
х |
|
при |
2 х 2, |
|
|
|
|
|||||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
1 |
при |
х |
2. |
||||
Определить: 1) плотность вероятности f(х), 2) вероятность того, что случайная величина примет значение в промежутке [0; 2].
Решение. 1. Определяем плотность распределения. Так как плотность вероятности есть производная от функции распределения (см.(4.8)), то вне интервала (-2; 2) плотность вероятности равна нулю. Найдем плотность
вероятности для всех х, |
принадлежащих интервалу |
|
|
|
||||||||||||||
(-2;2): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(х) = F (х) = |
1 |
|
2 |
arc tg |
x ' |
2 |
|
|
1 |
|
1 |
|
4 |
. |
||||
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
||||||
|
2 |
|
|
|
2 |
|
|
1 |
|
2 |
|
x2 |
4 |
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, искомая плотность имеет вид:
|
0 |
при х |
2, |
|
f(х) = |
4 |
|
при |
2 х 2, |
|
|
|||
|
|
|||
|
(х2 4) |
|
||
|
0 |
|
при х |
2. |
2. Вероятность того, что случайная величина примет значение на отрезке [0; 2], равна приращению интегральной функции распределения на этом промежутке (см.(4.11)). Следовательно,
Р(0 Х 2) = F(2) – F(0) = |
1 |
|
2 |
arc tg 1 |
1 |
|
2 |
arc tg 0 |
1 |
|
2 |
|
|
|
1 |
|
1 |
. |
2 |
|
2 |
|
2 |
|
|
4 |
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
Тогда искомая вероятность Р(0 Х 2) = 0,5.

37
Задача 6. Найти функцию распределения непрерывной случайной величины, плотность распределения вероятностей которой задана функцией
0 при х 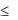 6 ,
6 ,
f(х) = 3sin 3 х при |
|
х |
|
, |
6 |
3 |
0 при х  3 .
3 .
Решение. Применяя формулу (4.10), найдем функцию распределения.
Если х |
6 , то F(х) = 0, так как f(х)=0 в этом промежутке. Если |
6 x 3 , |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
то F(х)= |
x f (t) dt |
60 dt |
x 3 sin 3t dt |
cos 3t |
|
|
cos3x. Если х> |
3 |
, то |
||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F(х)= x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||
f (t) dt |
60 dt |
3 3 sin 3t |
dt |
0 dt |
cos 3t |
cos |
cos |
|
|
1. |
|||||
|
2 |
|
|||||||||||||
|
|
|
6 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
при х |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|||||
|
|
F(х) = |
cos3х |
при |
6 х |
3 , |
|
|
|
|
|||||
1при х  3 .
3 .
За д а ч и
1.Выпущено 1 000 билетов денежной лотереи. При этом разыгрываются один выигрыш в 1 000 рублей, пять выигрышей по 500 рублей, двадцать выигрышей по 50 рублей. Составить ряд распределения стоимости выигрыша для владельца одного лотерейного билета. Построить полигон распределения. Найти функцию F(х) и построить ее график.
2.Монета брошена 4 раза. Составить ряд распределения случайной величины Х – частоты появления герба. Построить полигон распределения. Найти функцию F(х) и построить ее график.
3.Составить закон распределения случайного числа попадания кольца на колышек при одном броске, если вероятность попадания кольца на колышек у игрока равна 0,7. Указать функцию F(х) и построить ее график.
4.Рабочий обслуживает три станка. Вероятность того, что в течение часа первый станок потребует внимания рабочего, равна 0,15; для второго и третьего станков эти вероятности равны, соответственно, 0,2 и 0,25. Составить ряд распределения числа станков, которые потребуют внимания рабочего в течение часа.

38
5.Охотник, имеющий 4 патрона, стреляет в цель одиночными выстрелами до первого попадания или пока не израсходует все патроны. Составить ряд распределения случайной величины Х – количества израсходованных патронов, если вероятность попадания при каждом выстреле равна 0,6.
6.Вероятность изготовления нестандартного изделия при производстве некоторой продукции составляет 5%. Для проверки качества изделий контролер из всей партии случайно выбрал 5 изделий и должен проверять их до обнаружения нестандартного. Составить закон распределения числа изделий, проверяемых контролером.
7.В партии из восьми деталей пять стандартных. Наудачу отбираются три детали. Составить закон распределения числа стандартных деталей среди отобранных.
8.Построить график функции распределения
|
|
0 |
|
|
при х |
1, |
||
F(х) = |
1 |
х |
1 |
|
при |
1 |
х 2, |
|
3 |
3 |
|||||||
|
|
|
|
|
||||
|
|
1 |
|
|
при |
х |
2. |
|
Найти плотность распределения вероятностей и построить ее график. Вычислить вероятность попадания случайной величины в интервал (0,
1).
9. Функция распределения непрерывной величины Х задана выражением
|
0 при х |
0, |
|
|
||
F(х) = |
1 cos 2 х |
при 0 |
х |
|
, |
|
2 |
2 |
|||||
|
|
|
|
|||
1 при х |
|
. |
|
|
2 |
|
|
||
Найти плотность вероятности f(х) и построить ее график. |
|
|
||
|
|
|
A |
|
10.Случайная величина Х распределена по закону Коши: f(х)= |
|
. |
||
1 x2 |
||||
Найти: 1) коэффициент А; 2) функцию распределения F(х); 3) построить |
||||
графики f(х) и F(х); 4) вероятность попадания величины Х на интервал
1; 
 3 .
3 .
11. Дана плотность вероятности случайной величины:
0 |
при х |
3, |
|
f(х) = 13 |
при |
3 |
х 6, |
0 |
при |
х |
6. |
Требуется: 1) найти функцию распределения; 2) построить графики функций f(х) и F(х); 3) вычислить вероятность того, что значение случайной величины будет находиться в интервале (2; 5).
