Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Хабаровский государственный университет экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5520.pdf

Скачиваний:

Добавлен:

13.11.2022

Размер:

1.72 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1510 11 12 13 14 15 > Следующая >>>

Легко установить, что


	xВ = U h + c,					(9.12)
					)2 ]h2.
ДВ = [		U 2	(			(9.13)
				U

Метод произведений есть некоторый удобный способ вычисления условных моментов различных порядков в случае равноотстоящих вариант. По условным моментам можно найти начальные и центральные эмпирические моменты. Вычислять условные моменты

U k легко, так как условные варианты Ui есть целые числа. В частности, по формулам (9.12) и (9.13) можно вычислить xВ и ДВ.

Максимальная простота вычислений достигается, если в качестве ложного нуля С выбрать варианту, которая расположена примерно в середине вариационного ряда.

Размахом варьирования R называют разность между наибольшей и наименьшей вариантами:

R = хmax – xmin.

(9.14)

Размах есть самая простая характеристика рассеяния вариационного ряда. Еще одной характеристикой рассеяния служит среднее абсолютное отклонение , которое определяется равенством

	r
	ni	xi		xB
=	i 1					.	(9.15)
=		n				.	(9.15)
		n
Коэффициент вариации V определяется по формуле
	V =		B		100% .		(9.16)


			xB

Он служит для сравнения величин рассеяния двух вариационных рядов. Большее рассеяние имеет тот ряд, у которого коэффициент вариации больше.

Важными числовыми характеристиками являются мода и медиана. Для дискретного статистического ряда мода есть значение

признака, имеющего наибольшую частоту.

Определим теперь моду интервального ряда в случае постоянной длины h всех интервалов. Пусть (хk, хk+1) – модальный интервал, т.е. интервал, которому соответствует наибольшая частота nk. Пусть nk-1 – частота интервала, предшествующего модальному, а nk+1 – частота интервала, следующего за модальным. Тогда мода М0 вычисляется по формуле

М0 = хk + h		nk	nk 1			.	(9.17)
М0 = хk + h	(n	n	) (n	n	)	.	(9.17)
	k	k 1	k	k 1

Медианой Ме называется такое значение признака, относительно которого статистический ряд делится на две части, причем в одной из них содержатся члены, у которых значения не больше Ме, а в другой – члены со значениями не меньше чем Ме.

Пусть выборка дискретна и значения признака различны. Если

число вариант четное (n=2k), то
Ме =	xk xk 1	.	(9.18)
Ме =	2	.	(9.18)
	2

Если число вариант нечетное (n=2k+1), то

Ме = хk+1 . (9.19)

Пусть выборка дискретна и значения признака повторяются. Если объем статистической совокупности является нечетным числом, то в качестве медианы берут такое значение признака Х, для которого

накопленная частота SH (сумма частот вариант, не превосходящих

данного значения) равна		SH =	n	1, где квадратные скобки

			2
			2
показывают, что от числа	n	нужно взять только целую часть.
показывают, что от числа	2	нужно взять только целую часть.
	2

Если объем выборки является четным числом, то Ме определяется равенством

				Ме =		xS H' xS H"	,	(9.20)
				Ме =		2	,	(9.20)
						2
где xS H'	- первое значение признака,					для которого накопленная частота
SH' не	менее	n	и x "	- первое		значение		признака, для которого
SH' не	менее		и x "	- первое		значение		признака, для которого
	2		S H
	2
накопленная частота SH""				не менее	n	1.
накопленная частота SH""				не менее	2	1.
					2

Если статистический ряд задан интервалами, то медиану находят следующим образом. Выявляют первый интервал, для которого накопленная частота равна или больше половины объема

статистической совокупности			n		.	Этот интервал	называется
статистической совокупности			2		.	Этот интервал	называется
			2
медианным. Величину медианы определяют по формуле
	n	Sk 1

Ме = xk	2			(xk 1		xk ) ,	(9.21)
	2
		nk
		nk

где хk- левая граница медианного интервала; Sk-1 частота интервала, предшествующего медианному; медианного интервала.

Асимметрия 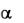и эксцесс 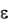эмпирического определяются равенствами:

m33 ,

m4	3	,
4

– накопленная nk – частота

распределения

(9.22)

(9.23)

где m3, m4 – центральные эмпирические моменты, соответственно, третьего и четвертого порядка. Эти характеристики используют для оценки отклонения эмпирического распределения от нормального.

Р е ш е н и е т и п о в ы х з а д а ч

Задача 1. Выборка шарикоподшипников, изготовленных станкомавтоматом, дала после измерения на весах следующие результаты в граммах: 39, 41, 40, 40, 43, 41, 44, 42, 41, 41, 43, 42, 39, 40, 42, 43, 41, 42, 41, 39, 42, 42, 41, 42, 40, 41, 43, 41, 39, 40. Составить статистическое распределение выборки. Построить полигоны частот и относительных частот.

Решение. Значения хi вариант выборки (вес шарикоподшипников) расположим в порядке возрастания в первой строке таблицы, а во второй строке – количество шарикоподшипников этого веса (частоты):

	хi	39	40	41	42	43	44
	ni	4	5	9	7	4	1
Получили дискретное статистическое					распределение выборки объема
n= ni = 4+5+9+7+4+1=30.		Мода М0=41.

Построим полигон частот. Для этого откладываем по оси Ох значения хi вариант выборки, а по оси ординат – частоты ni. Полученные точки соединяем отрезками прямых. Это и будет полигон частот (см.рис. ниже). ni




0	39	40	41	42	43	44	х

Полигон относительных частот строится аналогично полигону частот. На оси ординат вместо частот ni откладываем относительные частоты Wi. Полигон относительных частот изображен ниже на рисунке.

Задача 2. Составить статистическое распределение выборки – рабочих по процентам выполнения норм выработки, если произведена случайная выборка объема 20 человек и получены такие данные относительно выполнения ими норм выработки в процентах: 127, 121, 112, 114, 131, 117, 109, 107, 155, 135, 103, 145, 99, 100, 97, 102, 122, 115, 132, 105. Построить гистограммы частот и относительных частот.

Решение. Находим наибольшее и наименьшее значения варианты Х: хнаиб=155, хнаим=95. Разобьем здесь объем выборки на 7 промежутков длиной h=10. Частичные промежутки расположим в первой строке таблицы, а во второй – количество рабочих, чья выработка заключена в данном частичном промежутке. Получим следующее интервальное распределение:

Процент нормы	90-100	100-110	110-120	120-130	130-140	140-150	150-160
выработки
рабочих
Частоты (ni)	2	6	4	3	3	1	1

Построим гистограмму частот распределения. Для этого по оси Oх отложим промежутки распределения выборки и на них как на основаниях

строим прямоугольники, высоты которых равны соответственно nhi .

Гистограмма частот изображена на рисунке ниже.

									78
0	90	100	110	120	130	140	150		160					х
Нетрудно убедиться, что площадь построенных прямоугольников равна
объему выборки:
				7	ni	7
				h	ni	ni	2		6	4	3 3	1	1	20.
				h	h	ni	2		6	4	3 3	1	1	20.
				i 1	h	i 1
Гистограмму относительных частот строим аналогично гистограмме
частот. Только на оси ординат вместо										ni откладываем значения Wi , где Wi
										h				h
– относительные частоты соответствующих частичных промежутков.
Изображение гистограммы относительных частот см. на рисунке.
Wi
h
0	90	100	110	120	130	140 150		160						х
Сумма площадей построенных прямоугольников равна единице.
Задача 3. Данные о продаже женской обуви в магазине за день заданы
таблицей
				Размер			35		36	37	38	39	40
				обуви
				Количество			4		5	9	7	4	1
				проданных
				пар
Найти эмпирическую функцию распределения выборки и построить
ее график.
Решение.		Эмпирическую функцию распределения выборки находим по
формуле (9.1). Объем выборки равен											4+5+9+7+4+1=30. Наименьшая
варианта равна 35.				Значит,		F*(х)=0 при х 35. Значения Х<36, т.е. х1=35

наблюдались 4 раза. Следовательно, F*(х)=							4		при 35< х				36. Значения
наблюдались 4 раза. Следовательно, F*(х)=							30		при 35< х				36. Значения
							30
Х<37 (х1=35, х2=36) наблюдались 4+5=9 раз. Следовательно, F*(х)=														9	при
															при
													30
36< х	37.		Аналогично находим: F*(х) =				4	5 9		18		при	37< x		38;
36< х	37.		Аналогично находим: F*(х) =					30		30		при	37< x		38;
								30		30
F*(х) =		4	5 9 7		25	при 38< х 39;		F*(х) =			29	при 39< х			40.
F*(х) =			30	30		при 38< х 39;		F*(х) =		30		при 39< х			40.
			30	30						30

Так как х=40 – наибольшая варианта,					то F*(х)=1 при х>40. Запишем
эмпирическую функцию:
			0	при	х	35,
	4			при 35		х	36,

	30
	30
	9			при 36		х	37,

	30
	30
F*(х) =	18		при 37			х	38,

	30
	30
		25		при 38		х	39,
	30			при 38		х	39,
	30
		29	при 39			х	40,
	30		при 39			х	40,
	30
			1	при х		40.

График этой функции изображен на рисунке. y

0								х
Задача 4. Распределение урожайности сои на площади в 1000 га
дано в таблице
	Урожай с га в	9	9,6	10	10,5	11,4	12
	центнерах
	Число га	80	100	120	160	200	340

Определить выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение урожайности сои.

Решение. Выборочная средняя урожайности с га вычисляется по формуле (9.4):

	=	9 80 9,6 100 10 120 10,5	160 11,4 200 12 340	10,9 (ц).
xВ
		1 000

Для определения выборочной дисперсии воспользуемся формулой (9.6). Получим

ДВ =		80(9	10,9)2	100(9,6	10,9)2	120(10	10,9)2	160(10,5	10,9)2
ДВ =						1 000
						1 000
+	200(11,4		10,9)2	340(12	10,9)2	1,04.
+			1 000			1,04.
			1 000

		80
Выборочное	среднее	квадратическое отклонение В находим по

формуле (9.8):	В = 1,04	1,02.

Задача 5. Вычислить выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение и коэффициент вариации для распределения заработной платы водителей автобазы (в руб. за месяц):

Зарплата	200-250	250-300	300-350	350-400	400-450	450-500
(руб./месяц)
Количество	10	30	20	20	10	10
водителей

Решение. Превратим данный интервальный ряд в дискретный, взяв в качестве вариант середины интервалов:

Зарплата	225	275	325	375	425	475
(руб./месяц)
Количество	10	30	20	20	10	10
водителей

По формуле (9.4) выборочной средней найдем, что

				=	10 225 30 275 20 325 20 375 10 425	10 475	335.
		x	В		10 225 30 275 20 325 20 375 10 425	10 475
		x
				100
				100
Вычислим выборочную дисперсию по формуле (9.7):
ДВ =	10 2252 30 2752 20 3252 20 3752 10 4252					10 4752	3352 5 400.
ДВ =				100			3352 5 400.
				100

Извлекая корень квадратный из дисперсии, получим выборочное среднее квадратическое отклонение В = 5400 73,5.

Коэффициент вариации заработной платы водителей автобазы вычислим по формуле (9.16):

V =	73,5	100% 21,9% .
	335

Задача 6. Дано следующее статистическое распределение выборки:

хi	3	5	6	8
ni	2	4	3	5

Вычислить начальные и центральные моменты первого, второго и третьего порядка, размах варьирования и среднее абсолютное отклонение.

Решение. Используя формулу (9.9), находим начальные моменты:

			2 3	4 5		3 6	5 8
		x1	2 3	4 5		3 6	5 8	6,

					14
					14
		2 32		4 52		3 62	5 82
	x2	2 32		4 52		3 62	5 82	39,
	x2			14				39,
				14
		2 33	4 53		3 63		5 83
x3		2 33	4 53		3 63		5 83	1 930,7.
x3				14				1 930,7.
				14

Центральные моменты вычисляем по формуле (9.10):

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1510 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.20221.68 Mб205515.pdf
#
13.11.20221.7 Mб25516.pdf
#
13.11.20221.71 Mб15517.pdf
#
13.11.20221.71 Mб35518.pdf
#
13.11.20221.71 Mб45519.pdf
#
13.11.20221.72 Mб05520.pdf
#
13.11.20221.72 Mб05521.pdf
#
13.11.20221.73 Mб15522.pdf
#
13.11.20221.73 Mб25523.pdf
#
13.11.20221.73 Mб15524.pdf
#
13.11.20221.73 Mб15525.pdf