
- •Содержание
- •Если события А, В, С совместны, то
- •Формула полной вероятности имеет вид
- •ТЕМА 3. ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ
- •Пусть С – постоянная величина. Тогда
- •Для вычисления дисперсии используется формула
- •Дисперсия обладает свойствами
- •Если случайная величина распределена по закону Пуассона, то
- •Плотность нормального распределения имеет вид
- •Дисперсия нормального распределения
- •Правило трех сигм записывается в виде равенства
- •1. Ошибка указания времени часами со скачущей минутной стрелкой имеет равномерное распределение. Определить вероятность того, что при определении времени ошибка не будет превышать 20 секунд.
- •В предельной форме утверждения теоремы Бернулли имеют вид
- •На практике для вычисления дисперсии применяется формула
- •Легко установить, что
- •Вычислим размах товарооборота по формуле (9.14). Получим, что
- •ТЕМА 10. СТАТИСТИЧЕСКИЕ ОЦЕНКИ
- •ТЕМА 11. КОРРЕЛЯЦИЯ И РЕГРЕССИЯ
- •Непосредственно из этого определения следует, что
- •Найденные из систем (11.16) и (11.17) параметры подставляют, соответственно, в (11.14) и (11.15). В итоге получим искомое теоретическое уравнение регрессии Y на Х, предполагаемая кривая которого выравнивает эмпирическую кривую регрессии Y на Х.
- •Уравнение (11.11) очевидным образом преобразуется к виду
- •ТЕМА 12. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

50
Пусть случайная величина Х принимает целые неотрицательные значения m=0, 1, 2, …с вероятностями
m |
|
|
Р(Х=m) = m ! e , |
0. |
(6.13) |
Такое дискретное распределение называется распределением Пуассона с параметром . При различных 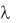 получим различные распределения. Функция F(х) этого распределения имеет вид
получим различные распределения. Функция F(х) этого распределения имеет вид
F(х) = |
0, |
|
если х |
0; |
|
(6.14) |
||
|
m |
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
e |
, если |
х |
0. |
|
|
m x m ! |
|
||||||
Если случайная величина распределена по закону Пуассона, то |
|
|||||||
М(Х) = |
, |
Д(Х) = |
. |
(6.15) |
||||
Дискретное распределение случайной величины Х, определяемое при фиксированном >0 формулой
m |
|
Р(Х=а+bm)= m! e , m 0,1, 2,... , |
(6.16) |
называется распределением пуассоновского типа. Из него получается распределение Пуассона при а=0, b=1.
Относительная частота W появления события А в независимых испытаниях есть случайная величина, которая может принимать значения
0, |
1 |
, |
2 |
, …, 1 с вероятностями |
|||
n |
n |
||||||
|
|
|
|
|
|||
|
|
|
|
Р W |
m |
Cnm pm (1 p)n m , m=0, 1, …, n. |
|
|
|
|
|
|
|||
|
|
|
|
n |
|||
|
|
|
|
|
|
||
Числовые характеристики относительной частоты появления события А в n независимых испытаниях, в каждом из которых оно может наступить с постоянной вероятностью р, имеют следующие значения:
М(W)=р, Д(W) = |
p (1 p) |
. |
(6.17) |
|
|||
|
n |
|
|
Р е ш е н и е т и п о в ы х з а д а ч
Задача 1. Составить закон распределения числа выпавших очков при однократном подбрасывании игральной кости. Определить тип распределения и найти числовые характеристики этой случайной величины.
Решение. Пусть Х – число очков, выпавших при однократном бросании игральной кости. Возможные значения этой случайной величины х1=1,
х2=2, х3=3, х4=4, х5=5, х6=6. Ясно, что Р(Х=хi)=1/6 для любого i=1,…,6.
Следовательно, ряд распределения имеет вид

|
|
|
|
|
51 |
|
|
|
|
|
|
Х |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
1 |
|
|
|
|
|
||||||
Р |
1/6 |
1/6 |
|
1/6 |
|
1/6 |
|
1/6 |
|
1/6 |
|
Получили пример равномерного дискретного распределения (см.формулу (6.1)). Его числовые характеристики находятся по формулам (6.3) и (6.4):
М(Х) = |
1 |
6 (1 |
6) 6 |
3,5; |
Д(Х) = |
12 |
62 |
(3,5)2 2,92. |
|||
|
6 |
|
|
2 |
6 |
|
6 |
||||
|
|
|
|
|
|||||||
Задача 2. Среди изготовленных за смену бригадой сборщиков десяти магнитофонов шесть – высшего качества. Для контроля случайным образом выбрали 3 изделия. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х – числа изделий высшего качества среди отобранных. Определить тип распределения.
Решение. Случайная величина Х принимает значения 0, 1, 2, 3. Вероятность того, что среди трех изделий, отобранных для контроля качества, окажется равно m(m=0, 1, 2, 3) изделий высшего качества, вычисляется по формуле (6.5). Тогда
Р(Х=0) = |
C 0 |
C3 |
1 |
, |
||||
C |
3 |
|
30 |
|||||
|
6 |
4 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
Р(Х=1) = |
C1 |
C 2 |
9 |
, |
||||
C |
3 |
|
30 |
|||||
|
6 |
4 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
Р(Х=2) = |
C 2 |
C1 |
15 |
, |
||||
C |
3 |
|
30 |
|||||
|
6 |
4 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
Р(Х=3) = |
C3 C0 |
5 |
|
|
||||
C3 |
4 |
|
30 . |
|||||
|
6 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
Таким образом, закон распределения этой случайной величины имеет вид
Х |
0 |
1 |
2 |
3 |
Р |
1/30 |
9/30 |
15/30 |
5/30 |
Это есть пример гипергеометрического распределения. Математическое ожидание и дисперсию найдем по формулам (6.6):
М(Х) = 3 |
|
6 |
1,8; |
Д(Х) = 3 |
6 |
1 |
|
6 |
1 |
|
3 |
0,56. |
|||
10 |
9 |
10 |
10 |
||||||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда (Х) = 0,56 |
0,748. |
|
|
|
|
|
|
|
|
|
|||||
Задача 3. Вероятность того, что покупатель, зашедший в обувной магазин, приобретет обувь 37 размера равна 0,4. Составить закон распределения случайной величины, выражающей число покупателей, которым необходима обувь 37 размера из первых зашедших в магазин шести покупателей. Определить тип распределения, математическое ожидание и дисперсию этой случайной величины.
Решение. Обозначим через Х случайную величину – число покупателей, которым необходима обувь 37 размера, среди первых шести вошедших. Она может принимать значения: 0, 1, 2, 3, 4, 5, 6. По условию задачи р=0,4,

52
q=0,6. По формуле Бернулли (6.7) определим вероятности, с которыми Х принимает соответственно значения 0, 1, 2, 3, 4, 5, 6:
Р(Х=0) = Р6 (0) = |
C60 |
(0,4)0 |
(0,6)6 |
= 0,046 656; |
Р(Х=1) = Р6 (1) = |
C61 |
(0,4)1 (0,6)5 = 0,186 624; |
||
Р(Х=2) = Р6 (2) = |
C62 |
(0,4)2 |
(0,6)4 |
= 0,31 104; |
Р(Х=3) = Р6 (3) = |
C63 |
(0,4)3 |
(0,6)3 |
= 0,27 648; |
Р(Х=4) = Р6 (4) = |
C64 |
(0,4)4 |
(0,6)2 |
= 0,13 824; |
Р(Х=5) = Р6 (5) = |
C65 |
(0,4)5 |
(0,6)1 |
= 0,036 864; |
Р(Х=6) = Р6 (6) = |
C66 |
(0,4)6 |
(0,6)0 |
= 0,004 096. |
Случайная величина имеет биномиальный закон распределения. Тогда числовые характеристики М(Х) и Д(Х) вычисляются по формулам (6.9).
Имеем: М(Х) = 6 0,4=2,4; Д(Х) = 6 0,4 0,6=1,44.
Задача 4. Охотник ведет стрельбу по дичи из автоматического ружья до попадания. Вероятность поражения дичи при каждом выстреле равна 0,7. Определить математическое ожидание и дисперсию числа произведенных выстрелов.
Решение. Случайная величина Х, выражающая число произведенных охотником выстрелов по дичи, может принимать следующие значения: х1=1, х2=2, х3=3, … .Охотник выстрелит по дичи один раз, если он в нее попадет, т.е. Р(Х=1)=р=0,7. Охотнику потребуется два выстрела, если при первом выстреле будет промах, а при втором – попадание в дичь. Вероятность такого случая равна q р=0,3 0,7=0,21. Следовательно, Р(Х=2)=0,21. Три выстрела потребуется охотнику, если при первом и втором выстрелах он промахнется, а при третьем попадет в дичь. Вероятность этого случая Р(Х=3)= q2 р=(0,3)2 0,7=0,063. И так далее. Таблица распределения вероятностей для числа произведенных охотником выстрелов по дичи имеет вид
Х |
1 |
2 |
3 |
|
Р |
0,7 |
0,21 |
0,063 |
|
|
|
|
|
|
Это есть пример геометрического распределения. Определим математическое ожидание и дисперсию по формулам (6.12):
М(Х) = 10/7, Д(Х) = 30/49.
Задача 5. Вероятность того, что расход воды на предприятии не превысит в рабочий день нормы, равна 0,8. Определить математическое ожидание и дисперсию случайной величины Х – числа дней, в которые произойдет перерасход воды среди первых пятнадцати дней месяца.
Решение. Случайная величина Х имеет биномиальное распределение. По условию задачи n=15, р=0,2, q=0,8. По формулам (6.9) находим математическое ожидание и дисперсию:
М(Х) = 15 0,2=3; Д(Х) = 15 0,2 0,8=2,4.

53
Задача 6. На автоматическую телефонную станцию за некоторое время Т поступает в среднем два вызова. Считая, что число вызовов в течение любого промежутка времени Т распределено по закону Пуассона, найти вероятности того, что в течение этого времени Т на телефонную станцию поступит m вызовов (m=0, 1, 2, …).
Решение. В качестве параметра 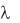 распределения Пуассона надо взять среднее число вызовов за время Т ( =2). Применяя формулу (6.13), получим:
распределения Пуассона надо взять среднее число вызовов за время Т ( =2). Применяя формулу (6.13), получим:
Р(Х=0) = |
20 e 2 |
|
|
1 |
|
|
||||||
0 ! |
|
|
|
|
e2 |
|||||||
|
|
|
|
|
|
|||||||
Р(Х=1) = |
|
|
21 e 2 |
|
2 |
|
||||||
1 ! |
|
|
|
|
e2 |
|||||||
|
|
|
|
|
|
|||||||
Р(Х=2) = |
|
22 e 2 |
|
2 |
|
|
||||||
2 ! |
|
|
|
|
|
e2 |
||||||
|
|
|
|
|
|
|
||||||
Р(Х=3) = |
23 e 2 |
|
|
4 |
|
|
||||||
|
|
3e2 |
||||||||||
|
|
3 ! |
|
|
|
|||||||
0,135 335;
0,27 067;
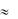 0,27 067;
0,27 067;
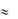 0,180 447.
0,180 447.
И так далее.
За д а ч и
1.Случайная величина означает число появлений герба при одном бросании монеты. Написать закон распределения вероятностей, определить его тип, найти числовые характеристики случайной величины.
2.Среди 15 измерительных приборов имеется 5 недостаточно точных. Для измерения наудачу выбирают 4 прибора. Случайная величина Х – число точных приборов среди отобранных. Определить вид закона и найти числовые характеристики.
3.Из 20 дипломных работ, среди которых 5 оценены аттестационной комиссией на «отлично», проверочная комиссия наугад отобрала 3 работы. Случайная величина Х – число дипломных работ, оцененных на «отлично» и оказавшихся в выборке. Определить вид закона этой случайной величины и найти ее числовые характеристики.
4.Покупатель приобрел 50 лотерейных билетов, вероятность выигрыша на каждый из которых равна 0,04. Х – число лотерейных билетов, на которые могут выпасть выигрыши. Указать тип распределения этой случайной величины. Найти М(Х) и (Х).
5.Вероятность попадания спортсмена по летящей мишени при каждом выстреле равна 0,8. Определить вид распределения и числовые характеристики случайной величины Х – числа попаданий спортсменом, если он произвел 20 выстрелов.
54
6.Для всхожести посеяли 80 семян перца. Гарантия всхожести составляет 90%. Найти математическое ожидание и среднее квадратическое отклонение числа взошедших семян.
7.Производится стрельба по цели до первого попадания с вероятностью попадания в отдельном выстреле, равной 0,2. Случайная величина означает число произведенных выстрелов. Указать, к какому теоретическому виду она относится. Найти математическое ожидание и дисперсию числа произведенных выстрелов.
8.Вероятность того, что из изготовленных изделий отдельно взятое изделие окажется дефектным, постоянна и равна 0,02. Контролер проверяет изделия до обнаружения дефектного. Случайная величина Х- число изделий, подвергнутых осмотру. Определить теоретический тип распределения и найти математическое ожидание случайной величины.
9.При некотором технологическом процессе в течение суток в среднем происходят три остановки. Число остановок при этом процессе в течение любых суток подчинено закону Пуассона. Найти вероятности, что в течение суток произойдет m остановок (m=0, 1, 2, …).

55
ТЕМА 7. ОСНОВНЫЕ НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
Равномерное непрерывное распределение на промежутке, его плотность вероятностей и функция распределения. Числовые характеристики равномерного распределения. Вероятность попадания равномерно распределенной непрерывной случайной величины на промежуток. Показательное распределение, его плотность и функция распределения. Числовые характеристики показательного распределения. Вероятность попадания показательно распределенной случайной величины в заданный промежуток. Нормальное распределение, его плотность вероятностей и функция распределения. Влияние параметров нормального распределения на вид нормальной кривой (кривой Гаусса). Нормированная кривая, нормированное нормальное распределение. Числовые характеристики нормального распределения. Вероятность попадания нормально распределенной случайной величины в заданный промежуток. Вычисление вероятности заданного отклонения нормально распределенной случайной величины. Правило трех сигм, его сущность и применение на практике.
Л и т е р а т у р а
[2], гл.3, § 1,2, гл.4, § 1,5; [3], гл.5, 5.8, гл.6; [5], гл.11, § 6, гл.12, § 2-7, § 13-15, гл.13, § 1-3; [6], гл.4, § 18, 19, гл.5, § 23, 24; [7], гл.12, § 29-32; [8], гл.4, § 3, 5; [9], гл.3, § 4, гл.4, § 1, 3, гл.5, § 1, 2; [11], гл.29, § 206, 207; [12], ч.2, гл.3, § 12; [13], гл.20, § 13, 15-20. [14], § 3, 3.7-3.10; [15], гл.6, § 1-3; [16], гл.2, 2.6-2.9.
О с н о в н ы е п о л о ж е н и я и ф о р м у л ы
Плотность равномерного на отрезке [a, b] непрерывного распределения (дифференциальная функция f(х)) выражается аналитически равенством
|
0, |
если |
х |
а; |
|
|
f(х) = |
1 |
, |
если |
а |
х b; |
(7.1) |
|
||||||
b a |
||||||
|
0, |
если |
х |
b. |
|
|
Интегральная функция F(х) этого распределения имеет вид
|
|
0, |
если |
х |
а; |
|
|
F(х) = |
x |
a |
, |
если |
а |
х b; |
(7.2) |
|
|
||||||
|
b |
a |
|
|
|
|
|
|
|
1, |
если |
х |
b. |
|
|
Числовые характеристики равномерного на отрезке [a, b] непрерывного распределения находятся по формулам
