
Сапунов Теория пластичности 2011 (1)
.pdf
AB , BC и т.д. Вершины шестиугольника будем называть, соответственно, режимами A , B , C и т..д Очевидно, что уравнения плоского напряженного состояния различны для различных режимов. Решение конкретных задач обычно требует рассмотрения пластического деформирования в разных режимах, реализующихся в тех или иных частях пластической зоны.При этом нетрудно ошибиться и выбрать неправильную компоновку различных областей напряженного состояния, что иногда приводит к неверным заключениям. Для выбора правильной конструкции решения необходимо тщательное построение согласованного поля скоростей деформаций.
Проведем построение решений для разных режимов.
Режимы AB и DE . Для режимов AB и DE главные напряже-
ния имеют разные знаки( s1s2 < 0 ) и |
условие пластичности при- |
|||||||
нимает вид |
|
|
|
|
|
|
||
|
s1 - s2 |
|
|
1 |
(sx - sy |
2 + 4t)2xy = tт Þ |
||
tmax = |
|
|
= |
|||||
2 |
|
|||||||
|
|
|
2 |
|
|
|||
Þ (sx - sy )2 + 4t2xy = 4t2т ,
т.е. тот же самый вид, что и в случае плоской деформации. Соответственно, все результаты, полученные при решении задачи о плоской деформации, полностью переносятся на случай тонкой пластинки. Отметим только, что в случае пластинки имеют место ограничения на величину главных напряжений, например, для режима DE : s1 < sт , s2 < sт .
Уменьшения |
толщины |
пластинки не происходит, поскольку |
xz = 0 . |
|
|
Режимы CD |
и EF . |
Для режима CD имеем: s1 = sт , |
0 < s2 <sт . Положим s1 - s2 = 2 sтc , где c = c (x , y) - неизвестная функция. Тогда сумму главных напряжений можем записать в форме уравнения
61
s1 + s2 = 2 sт k (1 - c ) ,
где k = sign s1 = sign s2 . Для режима CD имеем k = +1 , для режи-
ма EF - k = -1 .
Выписанные два уравнения относительно s1 , s2 действительно
представляют значения главных напряжений на данных режимах. Так, на режиме CD имеем:
2s1 = 2 sт (c +1 - c ) Þ s1 = sт ,
2s2 = 2 sт (1 - c - c ) Þ s2 = sт (1- 2c ) .
Таким образом, условие пластичности удовлетворено, если главные напряжения s1 , s2 представлены посредством функции
c = c (x , y) следующим образом:
s1 + s2 = 2 sт k (1 - c ) , |
(3.8) |
s1 - s2 = 2 sтc . |
|
Преобразование дифференциальных уравнений равновесия проведем по схеме, принятой в разд. 3.2.
Перейдем к напряжениям s x , s y и txy , используя их пред-
ставления через главные напряжения s1 , s2 . Будем иметь:
s |
x |
ü |
= sт [k(1 - c ±)ccos 2a ] , |
txy = sтc sin 2a , |
|
ý |
|||
sy þ |
|
|
||
где a = a (x, y) - угол между направлением s1 и осью x .
Подставим найденные значения напряженийs x , s y и txy в
дифференциальные уравнения равновесия. После некоторых преобразований находим два уравнения относительно двух неизвестных функций c = c (x , y) и a = a (x, y):
62

|
sin 2a |
¶a |
- (k + cos 2a |
¶a)= 0 |
, |
|
|||
|
|||||||||
|
|
|
¶x |
|
|
¶y |
(3.9) |
||
|
|
|
|
|
|
|
|
||
sin 2a |
¶ |
ln c - (k + cos 2a |
¶ |
)ln c + 2k |
¶a |
= 0 . |
|||
|
|
|
|||||||
|
¶x |
¶y |
¶y |
||||||
Исследование системы уравнений (3.9) с использованием общего (детерминантного) метода позволяет установить наличие только одного семейства действительных характеристик:
d y |
= - |
k + cos 2a |
, |
da |
= 0 . |
d x |
sin 2a |
|
|||
|
|
d x |
|||
Данное обстоятельство показывает, что система уравнений (3.9) является системой параболического типа.
Интегрируя дифференциальные уравнения характеристических линий, получаем:
|
|
a = С1 |
, |
|
|
|
|
|
(3.10) |
|
|
y = xtg êéa + (k +1 |
p) |
úù + C2 , |
|
|
|||
|
|
|
|
|
|||||
|
|
ë |
4 |
û |
|
|
|
|
|
где С1 , С2 |
- постоянные интегрирования. |
|
|
|
|||||
Согласно полученным уравнениям, характеристические линии |
|||||||||
являются |
|
прямыми, наклоненными |
к |
осиx |
под |
углом |
|||
êéa + (k +1 |
p) |
úù и, следовательно, |
совпадающими с линиями сколь- |
||||||
ë |
4 |
û |
|
|
|
|
|
|
|
жения, т.е. с прямыми траекториями главных напряжений (см. |
|||||||||
разд. 3.1, рис. 3.2). Для режима CD |
характеристики совпадают с |
||||||||
прямолинейными траекториями численно меньшего главного -на пряжения s2 . Для режима EF имеем, что s2 = -sт , k = -1 , и характеристики проходят по прямолинейным траекториям главного напряжения s1 .
63

Отметим, что система |
уравнений(3.9) допускает |
построение |
||
общего решения первого уравнения в форме: |
|
|||
y = xtg êéa + (k +1 |
p) |
úù + F (a ) , |
(3.11) |
|
ë |
4 |
û |
|
|
где F(a) - произвольная функция, определяемая из граничных условий.
Рассмотрение второго уравнения системы (3.9) с учетом уравнения характеристических линий (3.10)позволяет утверждать, что вдоль характеристической линии справедливо соотношение:
d ln c = - 2k |
¶a |
|
d x |
. |
|
|
|||
|
¶x sin 2a |
|||
Вычислим производную ¶a / ¶x , дифференцируя общее решение первого уравнения (3.11) по x , внесем ее в последнее соотношение и выполним интегрирование. Описанная процедура позволяет получить общее решение второго уравнения:
c = |
Y (a) |
, |
(3.12) |
2x + (1 - kcos 2a)F¢ a( ) |
где Y(a) - произвольная функция, определяемая из граничных условий.
Отметим очевидное решение
a = const , c = const ,
определяющее равномерное распределение напряжений.
Режимы C и F . Для рассматриваемых режимов можем записать, что s1 = s2 = k sт , где для режима C имеем k = +1 , а для режима F - k = -1 .
64

Переходя к напряжениям s x , s y и txy , получим:
sx = sy = ksт , txy = 0 .
Очевидно, что дифференциальные уравнения равновесия удовлетворяются, и рассматриваемые режимы отвечают равномерному гидростатическому напряженному состоянию в плоскости x , y .
Режимы A и D . Для рассматриваемых режимов имеем s1 = k sт , s2 = 0 (одноосное растяжение или сжатие).
Определяя напряжения s x , s y и txy , будем иметь:
sx ü |
= |
ks |
т |
(1 ± cos 2a , ) txy = |
ks |
т |
sin 2a . |
ý |
|
|
|||||
2 |
|
2 |
|
||||
sy þ |
|
|
|
|
|
Подставив найденные соотношения в дифференциальные уравнения равновесия, находим, что угол наклона главного напряжения s1 является постоянной величиной ( a = const ), что определяет поле однородного растяжения или сжатия.
Результаты, полученные для рассмотренных режимов, без труда переносятся на оставшиеся режимы с внесением соответствующих изменений в обозначениях.
Задачи
3.1. Бесконечная пластинка с круговым отверстием, растягиваемая симметрично относительно центра отверстия.
Решение с привлечением условия пластичности Мизеса - Генки. Очевидно,
что для рассматриваемой задачи касательное напряжение trj равно нулю, а нор-
мальные напряжения sr и sj являются главными напряжениями. Условие пла-
стичности Мизеса - Генки в главных напряжениях
s21 - s1s 2 + s22 = s2т
можно удовлетворить, полагая
65

|
æ |
|
p ö |
, |
|
||
s1 |
= s j = 2tт cos ç w - |
|
|
÷ |
(3.13) |
||
|
|
||||||
|
è |
|
6 ø |
|
|
||
|
æ |
|
p ö |
|
|
||
s2 |
= s r = 2tт cos ç w + |
|
|
÷ . |
|
||
|
|
|
|||||
|
è |
|
6 ø |
|
|
||
Подставив значения |
напряжений sr и sj |
в дифференциальное |
уравнение |
||||
равновесия
dsr + sr - sj = 0 dr r
и проведя некоторые преобразования, приходим к дифференциальному уравнению относительно функции w = w (r , j)º w (r )
( 3 + ctg w)w + 2 dr = 0 , r
3 + ctg w)w + 2 dr = 0 , r
решение которого имеет вид
r 2 = C e- w 3 , sin w
3 , sin w
где C - постоянная интегрирования.
Если принять, что на бесконечности растягивающее усилие (напряжение) рав-
но q , а контур кругового отверстияr = a |
свободен от нагрузки, то граничные |
|
условия будут иметь вид |
|
|
sr = 0 |
при |
r = a , |
sr ® q |
при |
r ® ¥ . |
Рассмотрение соотношений (3.13) показывает, что напряжение sr будет рав-
няться нулю только при w = p/ 3 ( 0 £ w £ p ). Соответственно, граничное условие на контуре кругового отверстия позволяет определить постоянную интегрирования C :
r 2 = |
C |
e- w 3 |
Þ C = |
3 |
a 2e p / 3 . |
|
sin w |
2 |
|||||
|
|
r = a, w= p / 3 |
|
|||
|
|
|||||
С учетом полученного |
значения постояннойC |
уравнение, определяющее |
||||
функцию w = w (r ), принимает вид
66
æ |
r ö |
2 |
|
ç |
|
÷ |
= |
|
|||
è |
a ø |
|
|
|
|
|
|
3 |
æ p |
ö |
|
|
|
3 |
1 |
|
ç |
|
- w÷ |
|
(3.14) |
||
|
3 |
|
|||||||
e |
|
è |
ø |
. |
|||||
2 |
|
sin w |
|
|
|
|
|
||
Отметим, что функция w = w (r ) не должна менять знак; это следует из выпи-
санного уравнения для w , поскольку (r / a 2)> 0 .
Определим значение w при r ® ¥ , представив (3.14) в более удобном виде:
3 æ |
a ö |
2 |
|||
|
ç |
|
÷ |
= e |
|
2 |
r |
||||
è |
ø |
|
|||
3 |
æ |
p ö |
||
ç w - |
|
÷ |
||
3 |
||||
|
è |
ø sin w . |
||
Поскольку функция w = w (r ) |
конечна ( 0 £ w £ p ), то ясно, что при r ® ¥ долж- |
|||||||
но быть w ® 0 (значение w ® p не подходит, так как в этом случае sr < 0 ). |
||||||||
Соответственно, выполнение граничного условия при r ® ¥ и w ® 0 |
приво- |
|||||||
дит к результату: |
|
|
|
|
|
|||
|
|
|
|
|
|
sr = q = sт . |
|
|
Отметим, |
что при r ® ¥ и w ® 0 имеем sj = sт . |
|
||||||
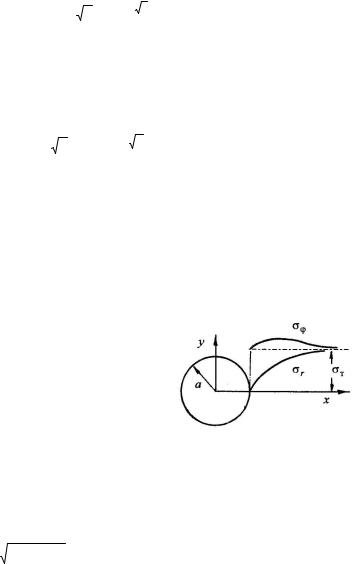
Распределение |
напряжений |
в пластине |
|
|||||
приведено на рис. 3.6. |
|
|
|
|
||||
Сопоставление |
полученного |
решения |
с |
|
||||
аналогичным упругим решением показывает, |
|
|
||||||
что если для упругой пластинки напряжение |
|
|
||||||
sj на |
круговом |
контуре |
равно 2q , т.е. |
|
|
|||
коэффициент концентрации напряжений -ра |
|
|
||||||
вен двум, то |
|
при переходе |
к пластическому |
Рис. 3.6 |
|
|||
состоянию он снижается до единицы. |
|
|||||||
|
|
|||||||
Перейдем к построению характеристических линий. Поскольку оси r |
и q - |
|||||||
главные, уравнения (3.7) принимают вид |
|
|
||||||
|
|
|
|
|
W ± q = const |
, |
|
|
|
w |
æ |
3 - |
|
|
ö |
|
|
где W = - ò |
ç |
4 cos 2 w / 2 sin w÷dw . Выписанные соотношения с учетом зави- |
||||||
|
p / 6 |
è |
|
|
|
ø |
|
|
симости (3.14) определяют уравнения характеристик в параметрической форме.
Для рассматриваемой |
задачи с |
ростом радиуса отr = a |
до r ® ¥ функция |
w = w (r ) уменьшается |
от w = p / 3 |
до нуля ( p/ 3 ³ w ³ 0 ). |
Соответственно, по |
67
мере удаления от контура кругового отверстия угол между характеристиками двух семейств (область гиперболичности) убывает, и при w = p/ 6 характеристики обе-
их |
семейств сливаются(точка параболичности). В интервале изменения w от |
p/ 6 |
до нуля решение определяется теми же уравнениями, но вещественных ха- |
рактеристик нет (область эллиптичности).
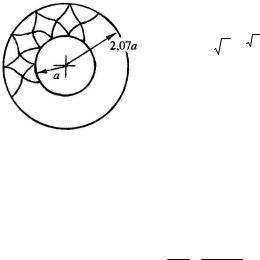
Построения характеристических линий показано на рис. 3.7.
Слияние характеристик имеет место при
æ |
r ö |
2 |
|
ç |
|
÷ |
= |
|
|||
è |
a ø |
|
|
|
3 |
æ p |
- |
p ö |
|||
3 |
ç |
|
|
÷ |
|||
3 |
6 |
||||||
2e |
è |
|
ø = 4,3 Þ r = 2,07a . |
||||
2 |
|
||||||
|
|
|
|
|
|
||
|
На примере рассматриваемой задачи видно, что, |
|
действительно, в теории плоского напряженного |
|
состояния пластическое равновесие может описы- |
Рис. 3.7 |
ваться как гиперболическими уравнениями, так и |
эллиптическими. |
Решение с привлечением условия пластичностиТреска - Сен-Венана. По-
скольку нормальные напряжения sr и sj являются главными напряжениями,
причем sj > sr , условие пластичности имеет вид sj = sт . Соответственно, дифференциальное уравнение равновесия
dsr + sr - sj = 0 dr r
можем разрешить относительно напряжения sr . Будем иметь:
dsr |
= - |
dr |
Þ ln (sr - sт |
= -) ln |
r |
Þ sr = sт + |
C |
. |
|
sr - sт |
r |
C |
r |
||||||
|
|
|
|
|
Граничные условия имеют тот же вид
sr = 0 |
при |
r = a , |
sr ® q |
при |
r ® ¥ . |
Граничное условие на контуре кругового отверстия позволяет определить постоянную интегрирования С = - sт a и записать окончательный вид соотношения
для напряжения sr :
æ |
|
a ö |
|
sr = sт ç |
1- |
|
÷ . |
|
|||
è |
|
r ø |
|
68

Соответственно, |
выполнение граничного условия |
при r ® ¥ приводит к ре- |
|
зультату: |
|
|
|
|
sr = q = sт . |
|
|
Распределение напряжений в пла- |
|
|
|
стине приведено на рис. 3.8. Можно |
|
|
|
видеть, что оно незначительно отлича- |
|
|
|
ется от соответствующего распределе- |
|
|
|
ния, полученного |
при использовании |
|
|
условия пластичности Мизеса - Генки. |
|
|
|
Система уравнений, рассматривае- |
|
|
|
мая в данном решении, соответствует |
Рис. 3.8 |
|
|
режимам типа CD , |
EF и т.п. и является системой параболического типа. |
Един- |
|
ственное семейство характеристик представляет собой пучок прямых, |
исхо- |
||
дящих из центра кругового отверстия (см. рис. 3.8). |
|
|
|
Очевидно, что если при r ® ¥ имеем q < sт , то, независимо от используемо-
го условия пластичности, пластическая область будет заполнять не всю плоскость вне кругового отверстия, а только некоторое кольцо между окружностью радиусом r = a и окружностью радиусом r = с , разделяющей пластическую и упругую области. В этом случае задача решается с привлечением условий непрерывности напряжений на границе раздела.
3.2. |
|
Бесконечная пластинка с круговым отверстием, по контуру |
|
|
которого действует равномерное давление. |
|
|
|
|
|
|
Будем |
рассматривать бесконечную пластинку с круговым отверстиемr = a , |
||
по контуру которого действует равномерное давление p . |
|||
При небольшой величине давления p пластинка находится в упругом состоянии и в полярной системе координат r , j напряжения sr и sj ( trj = 0 ) будут определяться известными соотношениями:
sr = - p (a / r 2) , |
sj = p (a / r 2) . |
Первые пластические деформации |
появятся на контуре кругового отверстия |
r = a . Давление pт , соответствующее первым пластическим деформациям, определится из условия пластичности, записанного для r = a . Используя, например, условие пластичности Треска - Сен-Венана, получим:
T = tmax = pт (a / r 2) |
= tт Þ p т = tт . |
|
r =a |
|
69

Этот же результат получим и при использовании условия пластичности Мизеса - Генки.
С возрастанием давления область пластического деформирования материала увеличивается и трансформируется в кольцо a £ r £ c , радиус c которого подлежит определению.
Очевидно, что в упругой области r ³ c напряжения должны определяться соотношениями:
ser = - tт (c / r 2) , sej = tт (c / r 2) .
Построение решения задачи в пластической областиa £ r £ c определяется используемым для этой цели условием пластичности.
Решение с привлечением условия пластичности Мизеса - Генки. Поскольку пластическая зона примыкает к круговому контуру, нагруженному равномерно распределенной нагрузкой, то напряженное состояние в этой зоне- осесимметричное.
Решение осесимметричной задачи с использованием условия пластичности Мизеса - Генки известно (см. задачу 3.1):
æ |
p ö |
, |
|
|
|
|||
s r = 2tт cos ç w + |
|
÷ |
|
C |
|
|||
6 |
|
|
||||||
è |
ø |
Þ |
r 2 = |
e- w 3 , |
||||
|
||||||||
æ |
p ö |
, |
|
sin w |
||||
s j = 2tт cos ç w - |
|
|
÷ |
|
|
|
||
6 |
|
|
|
|
||||
è |
ø |
|
|
|
|
|||
где C - постоянная интегрирования. |
|
|
|
|
|
|
|
|
||||||||
На границе раздела r = c |
упругой и пластической областей из условий непре- |
|||||||||||||||
рывности напряжений следует: |
|
|
|
|
|
|
|
|
|
|||||||
e |
|
|
|
r =c , |
|
|
æ |
|
p |
ö |
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
sr |
= sr |
|
|
|
- tт = 2tт cos ç w + |
|
|
|
÷ |
, |
p |
|
||||
|
|
|
|
|
|
|
||||||||||
|
r =c |
|
|
|
Þ |
è |
|
6 |
|
ø |
Þ w = |
. |
||||
sje |
|
|
|
|
|
æ |
p ö |
|
2 |
|||||||
|
|
|
|
|
|
|
|
, |
|
|||||||
= sj |
|
, |
|
|
tт = 2tт cos ç w - |
|
|
÷ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
r =c |
|
r =c |
|
|
è |
6 ø |
|
|
|
|
|||||
Соответственно, условие |
w = p/ 2 на контуре r = c |
|
позволяет определить по- |
|||||||||||||
стоянную интегрирования C : |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
C |
|
|
|
|
|
|
||||||||
|
r 2 = |
|
|
e- w 3 |
|
Þ C = c 2e p 3 / 2 . |
|
|
||||||||
|
|
|
|
|
|
|||||||||||
|
|
sin w |
|
r |
= c, w= p / 2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
70
