
Сапунов Теория пластичности 2011 (1)
.pdf
q = j ± p + mp , s = sn ± tт .
4
Для выбора знака необходимо учитывать дополнительные условия, определяемые механической (физической) постановкой рассматриваемой задачи. Некоторую помощь оказывает возможность судить о знаке нормального напряженияst = 2s - sn у контура C (см. рис. 2.7), что позволяет сделать правильный выбор решения.
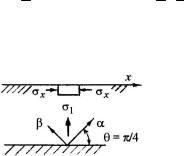
Например, для свободной прямолинейной поверхности (рис. 2.8) имеем:
j = p / 2 , sn = tn = 0 , |
Рис. 2.8 |
что позволяет получить:
q = p ± p + mp , s = ±tт Þ sx = st = ± 2 tт , sy = txy = 0 . |
|
2 |
4 |
Приведенный результат показывает, что вблизи границы может быть либо растяжение в направлении оси x , либо сжатие.
Задачи
2.1. Вдавливание плоского штампа в жесткопластическое полупространство.
Рассмотрим задачу о пластическом течении материала при вдавливании абсолютно твердого (жесткого) с плоским основанием в жесткопластическое тело, ограниченное плоскостью (рис. 2.9).
Будем считать, что трение на поверхности контакта отсутствует; при этом предполагается, что под штампом давление p - равномерное.
При вдавливании штампа выдавливаемый материал образует его сторонам возвышения и при развитом пластическом течении необходимо удовлетворять граничные
31
условия на деформированной поверхности. Здесь ограничимся рассмотрением начального пластического течения, когда ввиду малости пластических деформаций изменениями очертаний свободной поверхности можно пренебречь.
Решение Прандтля. Очевидно, что первые пластические деформации появятся в точках A и B сразу же после приложения нагрузки к штампу (см. рис. 2.9). Однако жесткость тела между двумя местными пластическими областями в окрестностях упомянутых точек вначале исключает вдавливание штампа. Вдавливание будет иметь место только после того, как нагрузка на штамп достигнет значения, необходимого для появления развитой пластической зоны вдоль всего основания штампа и части свободной поверхности, примыкающей к штампу.
Построение поля напряжений (поля линий скольжения) начнем со свободной поверхности справа от штампа. Как уже отмечено, некоторый ее участок BE должен быть пластическим, чтобы была возможность вдавливания штампа. Для свободной прямолинейной поверхности участка имеем (см. разд. 2.3):
j = p , sn = tn = 0 Þ q = p ± p + mp , s = ±tт Þ s x = -2tт , s y = txy = 0 . |
||
2 |
2 |
4 |
Знак «минус» для напряжения s x взят на том основании, что в направлении
BE происходит сжатие. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Линии скольжения пересекают свободную по- |
|||||||||||||
|
|
|
верхность |
BE |
под |
углами p/ 4 и |
5p/ 4 , причем |
||||||||||
|
|
|
линия |
a |
под |
углом p/ 4 |
(вправо |
на p/ 4 |
от на- |
||||||||
|
|
|
правления |
s1 ; |
рис. 2.10), |
а линия b под |
углом |
||||||||||
|
|
|
|
5p/ 4 (влево на p/ 4 |
от направления s1 ). |
|
|||||||||||
Рис. 2.10 |
Поскольку в области BDE имеем, что q = p/ 4 , |
||||||||||||||||
s = - tт , для параметра x вдоль линии скольжения a получим: |
|
|
|||||||||||||||
|
|
x = |
s |
- q Þ x = - |
1 |
- |
p |
. |
|
|
|
||||||
|
|
|
2tт |
|
|
|
|
|
2 |
|
4 |
|
|
|
|
||
Таким образом, под линией BE |
имеет место равномерное поле напряжений, |
||||||||||||||||
однако длина участка BE неизвестна, и построить поле линий скольжения в об- |
|||||||||||||||||
ласти BDE пока не можем. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рассмотрим теперь участок |
AB , для которого имеем: |
|
|
|
|||||||||||||
j = |
p |
, sn = - p , tn |
= 0 |
Þ q = |
p |
± |
p |
+ mp , s = - p ± tт . |
|
||||||||
|
2 |
|
|
||||||||||||||
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||||
32

Полученный результат позволяет утверждать, что под штампом тоже имеет место равномерное поле напряжений, причем линии скольжения пересекают участок AB под теми же углами p/ 4 и 5p/ 4 .
Итак, под линиями AB и BE расположены области равномерного напряженного состояния в форме треугольниковBDE и ABC . Поскольку эти два треугольника имеют общую точку B , то соединены они центрированным полем напряжений BCD (см. рис. 2.9). Отсюда следует, что длина пластического участка свободной поверхности BE равна ширине штампа 2a .
Отметим, что если в области BDE значения среднего напряжения s и угла q определены ( s = - tт , q = p/ 4 ), то в области ABC известен только угол q = - p / 4 (в соответствии с построенными полями линий скольжения). Для оты-
скания среднего напряжения воспользуемся тем обстоятельством, что вдоль линии скольжения a , проходящей, кстати, через все три рассматриваемые области, параметр x имеет постоянное значение. Будем иметь:
x ÑBDE = xÑABC |
Þ - |
1 |
- |
p |
= |
s |
+ |
p |
|
Þ s = - tт (1 + p) . |
|||
|
|
|
|
||||||||||
|
|
|
2 4 2tт |
4 |
|
|
|
||||||
Найденное значение среднего напряжения s = - tт (1 + p) |
вместе с известным |
||||||||||||
значением угла q = -p/ 4 |
позволяют |
|
определить |
напряжения в областиABC , |
|||||||||
используя соотношения (2.6). Будем иметь: |
|
|
|
|
|
||||||||
sx = s - tт sin 2q |
, |
|
|
|
|
|
|
|
sx = - ptт |
, |
|||
s y = s + tт sin 2q , |
Þ |
|
s y = - tт (2 + p) , |
||||||||||
txy = tт cos 2q |
, |
|
|
|
|
|
|
|
|
txy = 0 . |
|
||
Найденное поле напряжений подтверждает правильность выбранного направ-
ления линий скольжения a . Действительно, при |
txy = 0 имеем, что напряжения |
|
sx и s y - главные, но при этом s x > s y . Соот- |
||
ветственно, линия a должна |
быть направлена |
|
вправо на p/ 4 от направления s x |
(рис. 2.11), что |
|
совпадает с ранее принятым направлением. |
Рис. 2.11 |
|
Сила, вдавливающая штамп и приводящая к наступлению пластического течения при малых пластических деформациях (предельная нагрузка), будет равна:
P* = -s y × 2a = 2tт a (2 + p ).
33

Решение Хилла. При построении решения здесь также принимается, что по линии контакта имеет место равномерное давление p . Дан-
|
ное |
утверждение позволяет |
считать, что в об- |
|
ласти OCDEB (рис. 2.12) имеет место такое же |
||
Рис. 2.12 |
поле |
напряжений, как в |
областиACDEB |
решения Прандтля (см. рис. 2.9). |
|||
Отметим, что при этом длина пластического участка свободной поверхности BE равна половине ширины штампа a .
Очевидно, что по линии AOB , как и в решении Прандтля, будет действовать равномерное давление s y = - tт (2 + p), и предельная нагрузка P* имеет прежнее
значение: P* = 2tт a (2 + p .)
Различие в решениях Прандтля и Хилла проявляется при рассмотрении полей скоростей. Не приводя соответствующих построений, отметим, что в решении Хилла, в отличие от решения Прандтля, имеет место непрерывное поле скоростей в пластических зонах.
Возможно построение решения, являющегося комбинацией решений Прандтля и Хилла и содержащего произвольный параметр, характеризующий наложение областей OCB и OFA друг на друга.
Рассмотренная задача иллюстрирует неоднозначность решений с использованием модели жесткопластического тела. Поэтому при построении возможных полей скольжения необходимо привлекать различные дополнительные соображения и экспериментальные наблюдения. В частности, если рассмотреть решение соответствующей задачи теории упругости о давлении жесткого штампа на упругую полуплоскость, то следует отдать предпочтение решению Хилла, поскольку пластические зоны возникают в точках A и B и затем распространяются к середине штампа.
2.2. Сжатие пластического слоя между двумя параллельными жесткими шероховатыми поверхностями (плитами).
Задача о сжатии пластического слоя между двумя параллельными жесткими шероховатыми плитами (рис. 2.13) решена Прандтлем в предположении, что пластический слой выдавливается в стороны и течет от середины к краям, при-
Рис. 2.13 чем на поверхностях контакта возникают большие касательные напряжения, которые при развитых пластических деформациях могут достигать предела текучести tт .
34

Напомним, что решение задачи о плоской деформации при отсутствии объемных сил сводится к интегрированию дифференциальных уравнений равновесия
¶sx |
+ |
¶txy |
= 0 , |
¶txy |
+ |
¶sy |
= 0 |
|
|
|
|
||||
¶x |
¶y |
¶x |
¶y |
||||
при выполнении условия пластичности
(sx - s y )2 + 4t2xy = 4t2т .
Решение рассматриваемой задачи может быть построено проще, чем общее решение, опираясь на некоторые дополнительные соображения.
Продифференцируем первое уравнение равновесия по y , второе по x и вычтем из первого уравнения второе. Будем иметь:
|
|
|
¶2 |
(sx - s y = |
¶2t)xy |
- |
|
¶2txy |
. |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
¶x¶y |
|
|
¶x2 |
|
¶y 2 |
|
|||||||
Подставляя |
в полученное |
уравнение |
|
разность нормальных |
напряжений |
||||||||||
(sx - s y )= ± 2 |
t2т - t2xy , найденную из условия пластичности, получим |
диф- |
|||||||||||||
ференциальное уравнение относительно одной неизвестной функции txy (x, y): |
|||||||||||||||
|
± 2 |
¶2 |
|
t2т |
- t2xy = |
¶2txy |
|
- |
¶2txy |
. |
|
||||
|
¶x¶y |
¶x2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
¶y2 |
|
||||||
Будем считать, что толщина пластического слоя 2h существенно меньше его длины 2l . В этом случае можно считать, что касательное напряжение txy являет-
ся функцией только y , и определение txy (y) не составляет особого труда:
|
¶2txy |
= 0 Þ t |
xy |
(y)= C + C |
2 |
y . |
|
|
|||||
|
¶y2 |
1 |
|
|||
|
|
|
|
|
||
Для отыскания постоянных интегрированияC1 и |
|
C2 воспользуемся приня- |
||||
тым допущением о наличии на поверхностях контакта значительных касательных напряжений, равных пределу текучести tт . Упомянутое допущение реализуем в
форме граничных условий txy = ± tт при y = ±h , выполнение которых позволяет получить:
35

txy = tт y . h
Значения нормальных напряжений определим из дифференциальных уравнений равновесия, учитывая найденное значение функции txy (y) . Будем иметь:
¶sx |
= - |
tт |
Þ s |
x |
= - |
tт |
x + f |
(y ) , |
|
|
|
||||||
¶x |
|
h |
|
h |
1 |
|||
|
|
|
|
|
||||
¶s y = 0 Þ sy = f2 (x) . ¶y
Произвольные функции f1 (y) и f2 (x), входящие в соотношения для нор-
мальных напряжений sx и sy , определим, удовлетворяя условие пластичности.
Получим:
|
t |
т |
x + f |
(y )- f |
|
(x )= ± 2 t |
|
æ y ö |
2 |
||
- |
|
2 |
т |
1-ç |
|
÷ |
. |
||||
|
|
|
|||||||||
|
h |
1 |
|
|
è h ø |
|
|||||
|
|
|
|
|
|
|
|||||
Перепишем полученное уравнение, оставляя слева функции переменной x , а справа - переменной y :
|
t |
т |
x - f |
|
(x )= - f |
(y )± 2 t |
|
æ |
y ö |
2 |
|
- |
|
2 |
т |
1-ç |
|
÷ . |
|||||
|
|
|
|||||||||
|
h |
1 |
|
è h ø |
|
||||||
|
|
|
|
|
|
||||||
Поскольку представленное уравнение должно выполняться при произвольных значениях переменных x и y , приходим к следующим двум соотношениям, оп-
ределяющим функции f1 (y) и f2 (x):
f2 (x )= - |
tт |
x + С , |
|||
|
|||||
|
h |
|
|
|
|
f1 (y )= ± 2 tт |
æ |
y ö |
2 |
||
1-ç |
|
÷ |
+ С , |
||
|
|||||
|
|
è h ø |
|
||
где С - произвольная постоянная. |
|
|
|
|
|
36

Окончательно, для напряжений имеем:
|
|
tт |
|
x ± 2 tт |
|
æ y ö |
2 |
|
|
||||||
|
sx = - |
|
|
1-ç |
|
÷ |
+ С , |
|
|||||||
|
h |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
è h ø |
|
|
(2.11) |
|||
|
|
|
|
|
|
tт |
|
|
|
|
|
|
|
||
|
|
|
sy |
= - |
x + С |
, |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
||
|
|
|
|
txy = |
tт |
|
y . |
|
|
|
|
||||
|
|
|
|
h |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В приведенных соотношениях знак « ± » |
отвечает двум возможным реше- |
||||||||||||||
ниям |
задачи, а постоянная С |
определяет |
значение напряженияsy |
при x = 0 . |
|||||||||||
При |
дальнейших рассмотрениях в |
формуле |
для напряжения sx |
оставляем |
|||||||||||
знак « + » [5].
Полученное решение в напряжениях (2.11) отвечает дифференциальным уравнениям равновесия, условию пластичности и граничным условиям по линиям контакта с плитами при любых значениях постояннойС . Следовательно, значение постоянной либо следует искать из граничных условий на торцах пластического слоя, которые свободны от нагрузки:
sx |
|
x=± l = 0 , |
txy |
|
x =±l = 0 , |
||
|
|||||||
|
|
|
|||||
либо из физического условия s y |
|
- при x = l давление на поверхностный |
|||||
|
= 0 |
||||||
|
|
|
|
x =l |
|
|
|
|
|
|
|
|
|
|
|
слой равно нулю.
Можно сразу видеть, что решение не позволяет точно(«жестко») удовлетворить представленные граничные условия при x = ± l . Остается вариант с их удов-
летворением в интегральном смысле. Соответствующие граничные условия имеют вид
+h |
+h |
ò sx d y = 0 , |
ò txy d y = 0 . |
-h |
-h |
Второе из выписанных граничных условий удовлетворяется тождественно, а первое после интегрирования и некоторых преобразований позволяет определить постоянную С :
|
æ l |
|
p ö |
|||
-tт l + tт hp/ 2 + С h = 0 Þ |
C =tт ç |
|
+ |
|
÷ . |
|
h |
2 |
|||||
|
è |
|
ø |
|||
37

Учитывая найденное значение постоянной С , можем определить напряжения (2.11) и предельную сжимающую нагрузку, отвечающую рассматриваемому состоянию развитой пластической деформации:
|
* |
|
l |
|
|
* |
æ |
l |
ö |
2P |
|
òs y dx |
|
|
|||||
|
= - 2 |
Þ |
2P |
|
= - tт l ç |
|
+ p ÷ . |
||
|
|
h |
|||||||
|
|
|
0 |
|
|
|
è |
ø |
|
|
|
|
|
|
|
|
|
|
Если же, не касаясь условий на торцах пластического слоя, принять во внимание требование о равенстве нулю давления плиты на поверхностный слой при x = l , получим новое значение постоянной:
s y |
|
= 0 Þ |
|
= |
tт |
l . |
|
C |
|||||
|
|
|||||
|
x=l |
|
|
|
h |
|
Предельная сжимающая нагрузка в этом случае будет равна:
|
|
* |
|
l |
2 |
|
|
2P |
= - tт |
. |
|||||
|
|
|
|||||
|
|
|
|
|
h |
||
Отметим, что построенное решение в напряжениях (2.11) в обеих вариантах (с постоянной C или C ) остается неудовлетворительным вблизи концов пластиче-
ского |
слоя (вблизи x = l ). Кроме того, на оси симметрии пластической полосы |
(при |
x = 0 ) касательные напряжения должны обращаться в нуль. Следует пола- |
гать, что такая ситуация связана с наличием жестких областей в средней части пластического слоя и на его концах.
Перейдем к построению поля линий скольжения. Напомним, что уравнения, определяющие линии скольжения a и b , имеют вид
d y |
= tgq и |
d y |
= - ctgq . |
|
|
||
d x |
dx |
||
Построение линий скольжения в рассматриваемой задаче существенно упрощается, поскольку имеется возможность формально связать переменныеy и q , сравнивая касательные напряжения, определяемые формулами (2.6) и (2.11):
txy = tт cos 2q , |
Þ |
d y |
= -2 h sin 2q |
¶q |
. |
||
|
|
Þ y = h cos 2q |
|||||
|
tт |
|
|
||||
txy = |
y , |
|
d x |
¶x |
|||
|
|
|
|
|
|
||
|
h |
|
|
|
|
|
|
38
Для линий скольжения, соответственно, имеем:
|
d y |
= tgq |
Þ |
2 h sin 2q |
¶q |
|
= - tgq |
- линии a ; |
||
|
|
|
|
|
||||||
|
d x |
|
|
|
¶x |
|
||||
d y |
= - ctgq |
Þ |
2 h sin 2q |
|
¶q |
= ctgq |
- линии b . |
|||
|
|
|||||||||
dx |
|
|
|
¶x |
|
|||||
Разделяя переменные и интегрируя, получим параметрические уравнения семейств линий скольжения:
x = -h (2q + sin 2q)+ const |
, |
y = h cos 2q |
- линии a ; |
|
x = -h (2q - sin 2q)+ const |
, |
y = h cos 2q |
- линии b . |
|
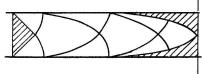
Приведенные уравнения определяют |
|
|
||
два ортогональных семейства |
циклоид |
|
||
с радиусом производящего круга, рав- |
|
|
||
ным h . Прямые |
y = ± h являются оги- |
|
|
|
бающими этих |
семейств циклоид. На |
|
|
|
рис. 2.14 показаны циклоиды для случая |
|
|
||
const = 0 . |
Рис. 2.14 |
|
Расчет скоростей перемещений и скоростей деформаций проводится при найденных соотношениях для напряжений с привлечением соответствующих уравнений теории пластического течения.
Напомним, что решение Прандтля построено в предположении, что толщина пластического слоя 2h существенно меньше его длины 2l ( l >> h ).
Для слоя конечной (средней) толщины или короткого слоя уже нельзя пренебрегать влиянием условий на концах слоя и в его центральной части. Соответствующие решения, имеющиеся в литературе, различают при l / h > 3,64 и
1 £ l / h £ 3,64 .
2.4. Плоская деформация в полярных координатах
Для плоского деформированного состояния при отсутствии объемных сил дифференциальные уравнения равновесия в полярной системе координат r , j принимают вид
¶s |
r |
+ |
1 |
|
¶trj |
+ |
|
sr - sj |
|
= 0 , |
||||||
|
|
|
r |
|
¶j |
|
|
r |
|
|||||||
¶r |
|
|
|
|
(2.12) |
|||||||||||
|
¶trj |
|
|
|
1 ¶sj |
|
2trj |
|||||||||
|
+ |
|
+ |
= 0 . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
¶r |
|
r ¶j |
r |
||||||||||||
|
|
|
|
|
|
|
||||||||||
39

В уравнения жения sr , sj и ности
равновесия (2.12) входят три неизвестных напря- trj . Добавив к этим уравнениям условие пластич-
(sr - sj )2 + 4tr2j = 4tт2 , |
(2.13) |
получим, как и в прямоугольной системе координат, три уравнения с тремя неизвестными.
Общее решение уравнений (2.12) и (2.13) строится совершенно аналогично тому, как это было сделано при исследовании задачи о плоской деформации в прямоугольных координатах.
Для частных задач решение в полярных координатах может быть упрощено с привлечением дополнительных условий, определяемых механической (физической) постановкой рассматриваемой задачи.
Задачи
2.3. Задача о нагружении толстостенной трубы внутренним давлением.
Решение упругопластической задачи о нагружении толстостенной трубы внутренним давлением для случая, когда материал не имеет упрочнения, подробно рассмотрено в работе [10 ], где получены соотношения, определяющие напряже-
ния в предельном состоянии и значение предельной нагрузки.
Получим эти же соотношения, используя представления о линиях скольжения. Напомним, что уравнения, определяющие линии скольжения a и b , имеют вид
d y |
= tgq и |
d y |
= - ctgq . |
|
|
||
d x |
dx |
||
Свяжем параметр линий скольжения(угол) q с переменной j . Угол q определяет положение площадки, где действует положительное максимальное касательное напряжение tmax , и связан с углом a , определяющим направление
главного напряжения s = s |
max |
относительно оси x , соотношением q = a - |
p |
|
|||
1 |
4 |
||
(рис. 2.15). |
|
||
|
|
|
|
40
