
- •Isbn 978-985-519-056-2 © бгату, 2009 Предисловие
- •Учебная программа по учебной дисциплине
- •Модуль 4 Аналитическая геометрия
- •Модуль 8 Функции нескольких переменных
- •Рекомендуемая литература Основная литература
- •Дополнительная литература
- •М одуль 1. Линейная алгебра
- •§ 1. Определители
- •С войства определителей.
- •§ 2. Матрицы
- •§ 3. Основные операции над матрицами
- •§ 4. Транспонированная матрица
- •§ 5. Обратная матрица
- •§ 6. Ранг матрицы. Элементарные преобразования матрицы
- •Контрольный тест
- •Задачи для самостоятельного решения
- •§ 1. Теорема Кронекера-Капелли
- •§ 2. Решение систем линейных уравнений
- •Контрольный тест
- •Модуль 3. Векторная алгебра
- •§ 1. Векторы. Операции над ними.
- •Сложение векторов.
- •Произведение вектора на число.
- •§ 2. Декартовы прямоугольные координаты вектора. Длина вектора.
- •§ 3. Скалярное произведение векторов.
- •Свойства скалярного произведения.
- •Контрольный тест
- •М одуль 4.
- •§ 1. Прямая на плоскости.
- •3 . Уравнение прямой в отрезках:
- •6 . Уравнение прямой, проходящей через данную точку и с заданным угловым коэффициентом:
- •§ 2. Взаимное расположение прямых на плоскости.
- •§ 3. Прямые в решениях экономических задач.
- •Контрольный тест
- •Модуль 5. Кривые второго порядка
- •§ 1. Окружность
- •§ 2.Эллипс
- •§ 3. Гипербола
- •§ 4. Парабола
- •Контрольный тест
- •М одуль 6. ФункциЯ одной переменной. Непрерывность функции одной переменной.
- •§ 1. Определение функции и способы её задания.
- •§ 2. Использование элементарных функций в экономике
- •§ 3. Предел числовой последовательности. Предел функции.
- •Односторонние пределы
- •§ 4. Теоремы о пределах.
- •З амечательные пределы
- •§ 3. Непрерывность функции.
- •Контрольный тест
- •§ 1. Производная функции,
- •§ 2. Таблица производных.
- •§ 3. Основные правила дифференцирования. Производная сложной функции.
- •Производная сложной функции.
- •Производная обратной функции.
- •§ 4. Правило Лопиталя и его применение к раскрытию неопределённостей.
- •§ 5. Признаки возрастания и убывания функций. Интервалы монотонности функций.
- •§ 6. Экстремум функции. Необходимый признак.
- •§ 7. Достаточные признаки экстремума функции.
- •§ 8. Наибольшее и наименьшее значения функции на отрезке.
- •§ 9. Выпуклость и вогнутость графика функции. Точки перегиба.
- •§ 10. Асимптоты графика функции.
- •§ 11. Общая схема исследования функции и построение её графика.
- •Контрольный тест
- •М одуль 8. Функции нескольких переменных
- •§ 1. Определение функции нескольких переменных
- •§ 2.Некоторые многомерные функции, используемые в экономике.
- •§ 3. Частные производные функции нескольких переменных.
- •§ 4. Экономический смысл частных производных
- •§ 5. Полный дифференциал функции нескольких переменных
- •§ 6. Частные производные и дифференциалы высших порядков
- •§ 7. Функция полезности
- •§ 8. Экстремум функции двух переменных
- •Контрольный тест
- •Краткий справочник
- •Простейшие формулы аналитической геометрии.
- •Плоскость и прямая в пространстве
- •Содержание
- •Высшая математика
- •Часть 1
- •Издано в редакции авторов
- •220023, Г. Минск, пр. Независимости, 99, к. 2
§ 2. Решение систем линейных уравнений
Метод Крамера
П
усть
система
из
линейных
уравнений
с
неизвестными записана в матричной
форме:
![]() ,
где
,
где
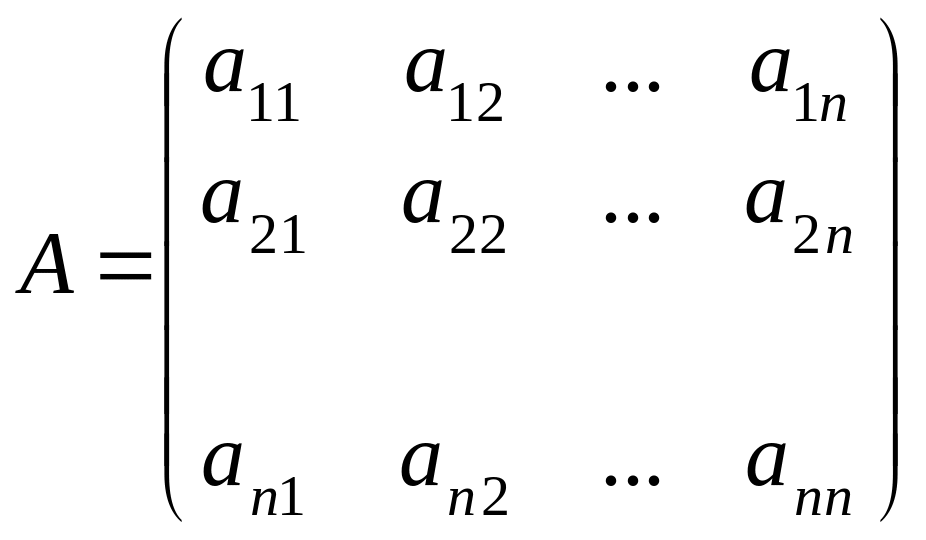 —
матрица системы,
—
матрица системы,
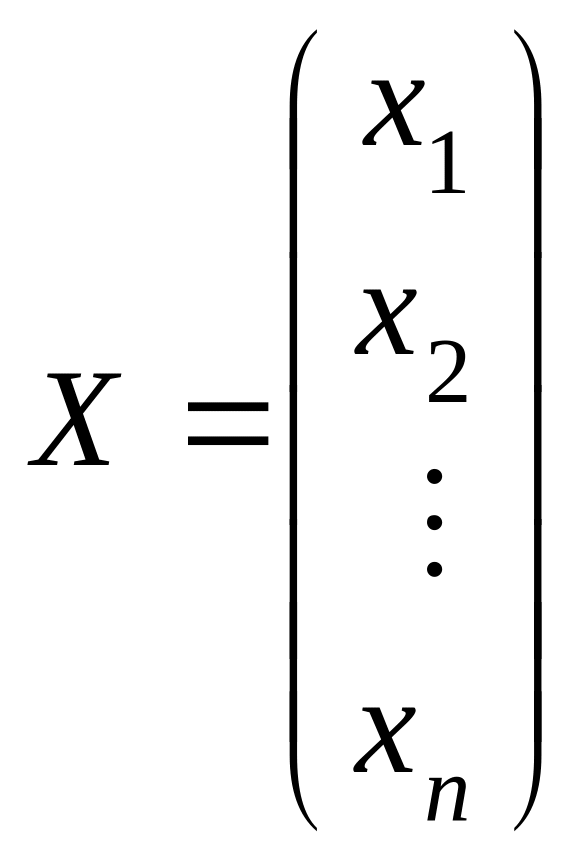 — столбец
неизвестных,
— столбец
неизвестных,
 —
столбец свободных членов.
—
столбец свободных членов.
Пусть
![]() —
определитель
матрицы
и пусть
—
определитель
матрицы
и пусть
![]() ,
т.е.
,
т.е.

П равило Крамера. Если определитель системы (1) , то эта система совместна и определённа, т.е. имеет единственное решение, получаемое по формулам:
где
|
Пример 2.1. Решите систему уравнений по формулам Крамера:
![]()
Н
айдём
определитель матрицы системы:
![]() .
.
Т.к. , то решение системы существует и единственно.
Найдём
определитель
![]() .
В определитель
вместо первого столбца
.
В определитель
вместо первого столбца
![]() подставим столбец свободных членов
подставим столбец свободных членов
![]() :
:
![]() .
.
Определитель
![]() получается из
подстановкой столбца свободных членов
вместо второго столбца
получается из
подстановкой столбца свободных членов
вместо второго столбца
![]() :
:
![]() .
.
Отсюда получим решение системы уравнений:
![]() ;
;
![]() .
.
О
твет:
![]()
М![]() атричный
метод
атричный
метод
Пусть система из линейных уравнений с неизвестными записана в матричной форме: , Тогда, если определитель , то система совместна и определённа, её решение задаётся формулой:
![]()
Пример
2.2.
Решите
систему уравнений
примера 2.1 с помощью обратной матрицы:
![]() .
.
Т .к.
 ,
то
решение системы существует и единственно.
,
то
решение системы существует и единственно.Найдём алгебраические дополнения к элементам матрицы
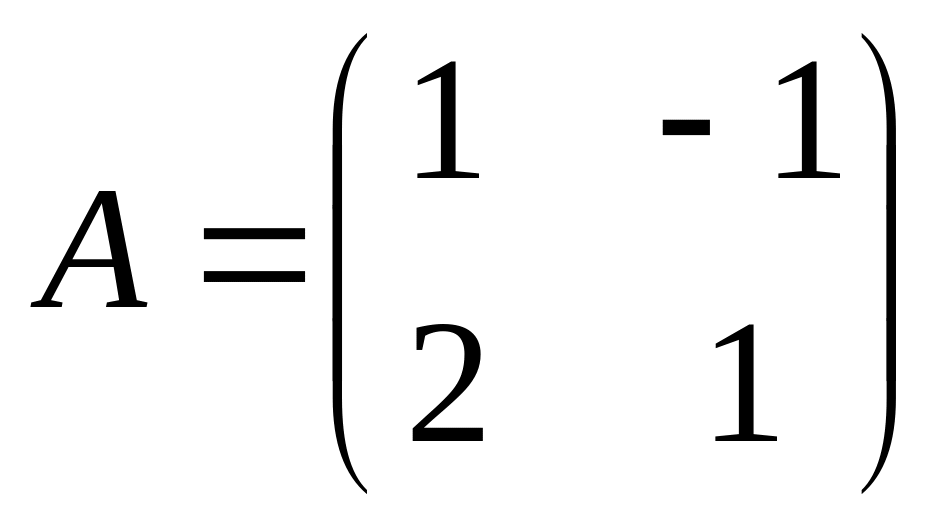 :
:
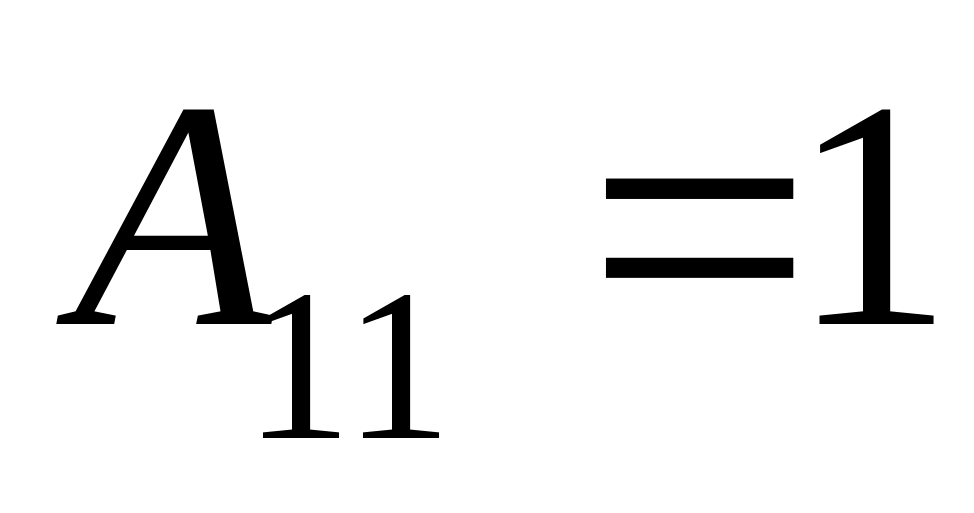 ,
,
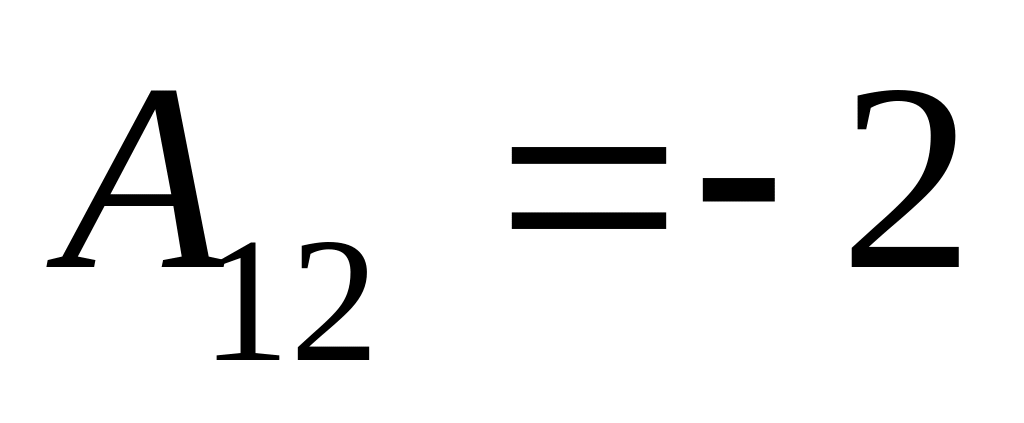 ,
,
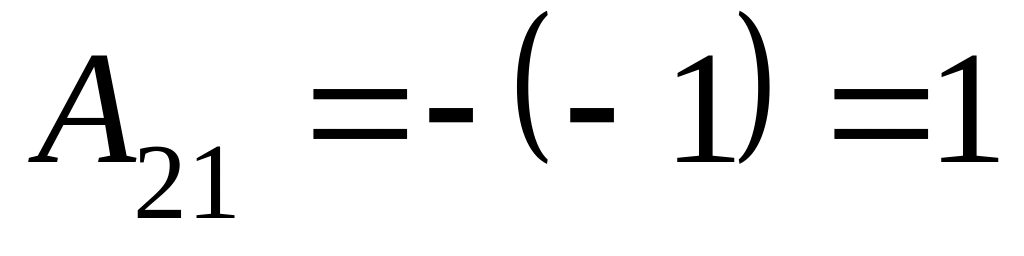 ,
,
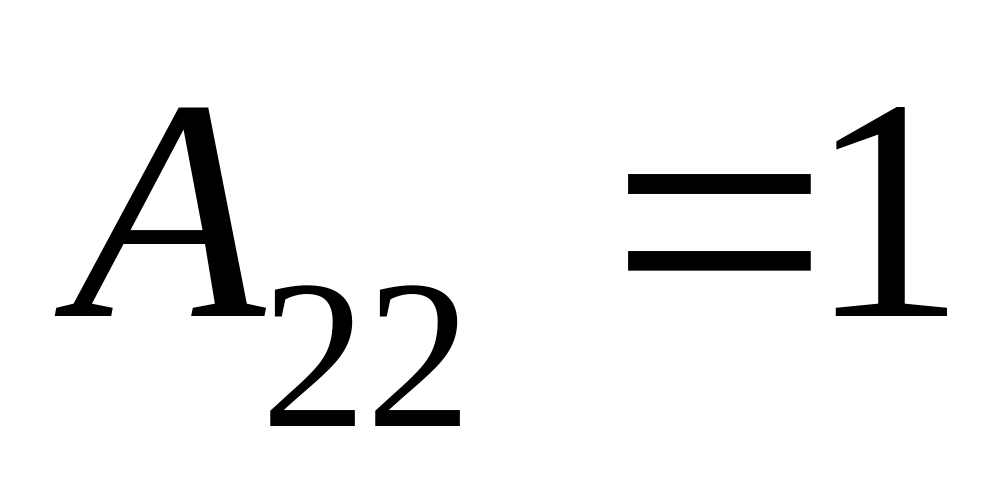 .
.Найдём присоединённую матрицу:
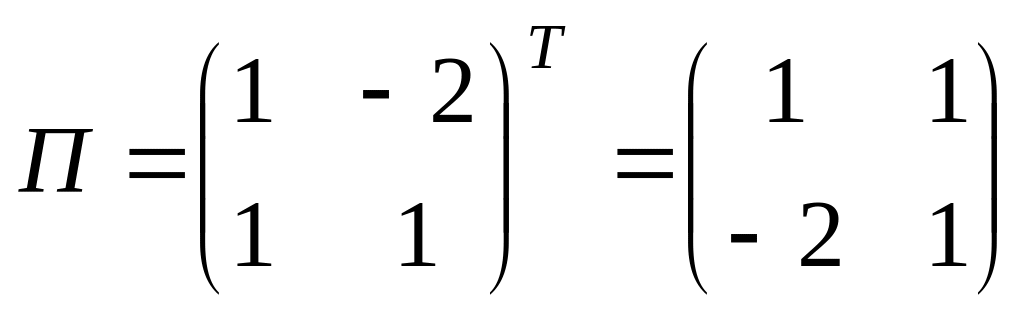 .
.Найдём матрицу :
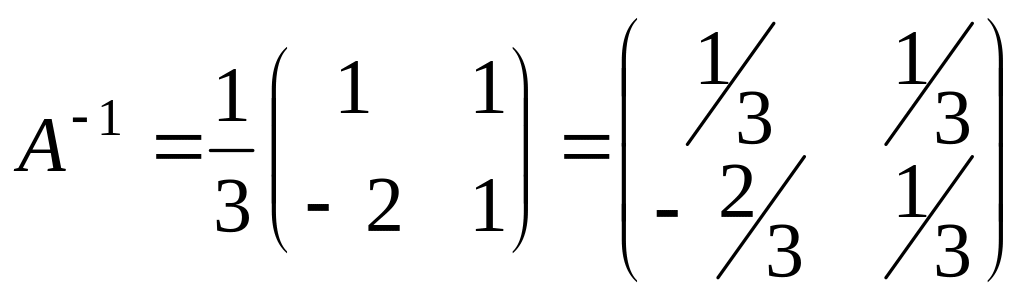 .
.Найдём решение системы уравнений:

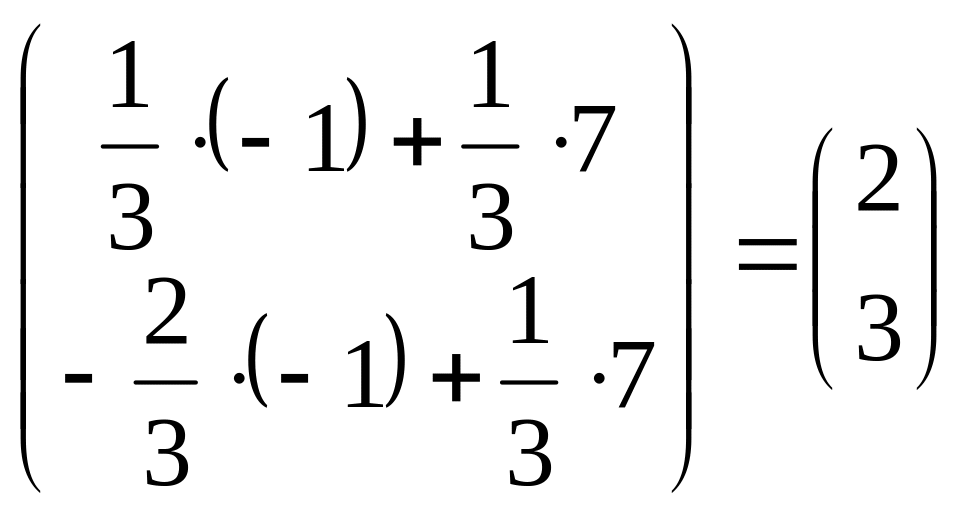 .
.
О
твет:
![]() .
.
Пример
2.3.
Решите
систему
уравнений по формулам Крамера и с помощью
обратной матрицы:![]()
I способ, метод Крамера.
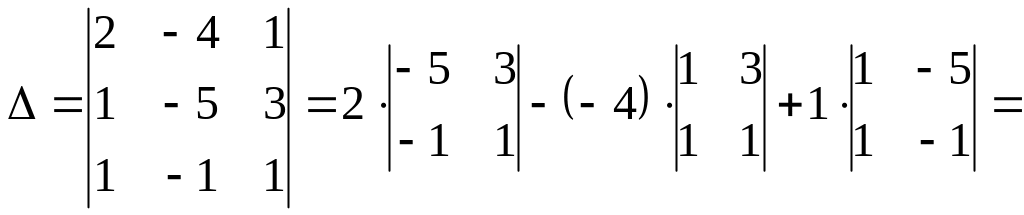
![]() .
.
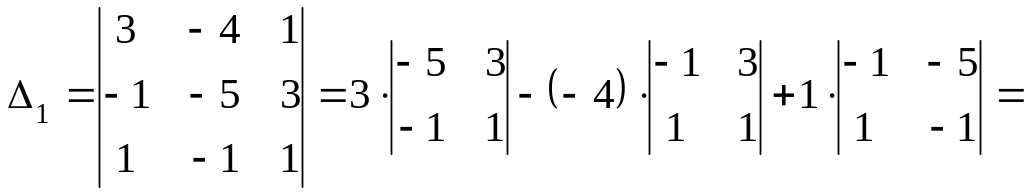
![]() .
.

![]() .
.

![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
О
твет:
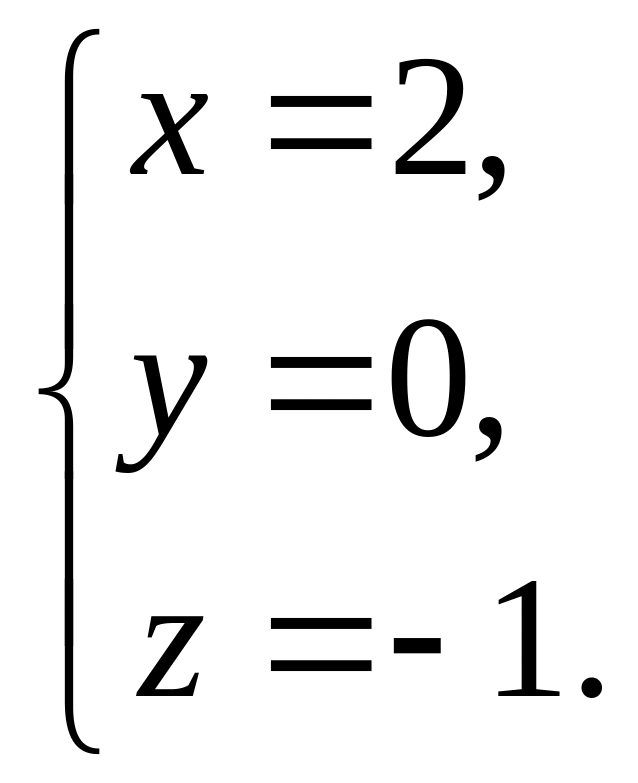
I I способ, метод обратной матрицы.
1)
![]() .
.
2)
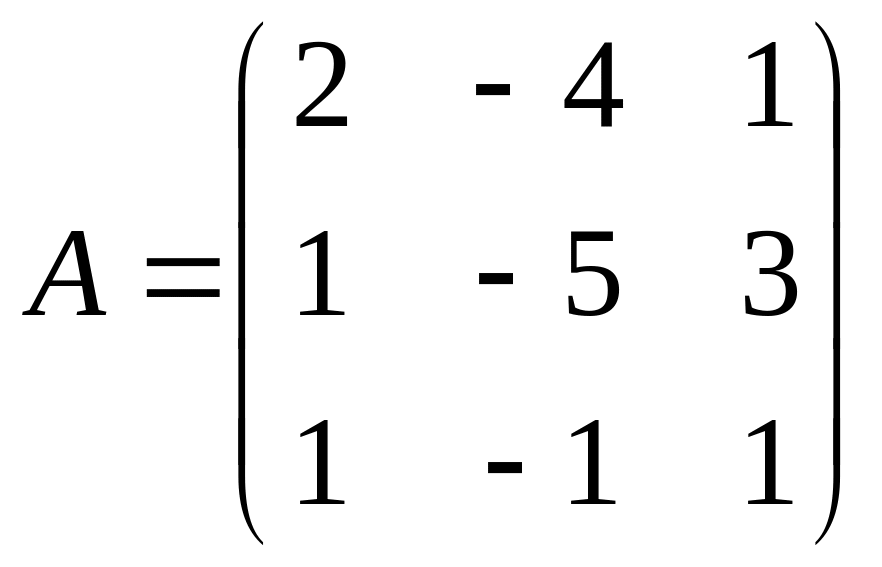
Алгебраические дополнения элементов матрицы :
![]()
![]()
![]()
3) Присоединенная матрица:
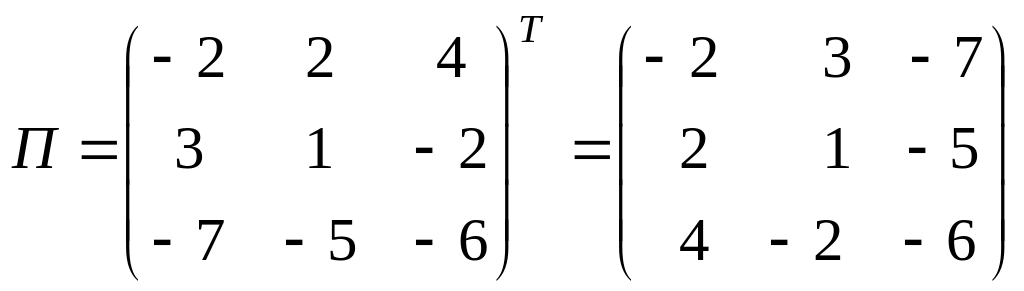 .
.
4) Обратная матрица:
![]() .
.
5) Решение системы:
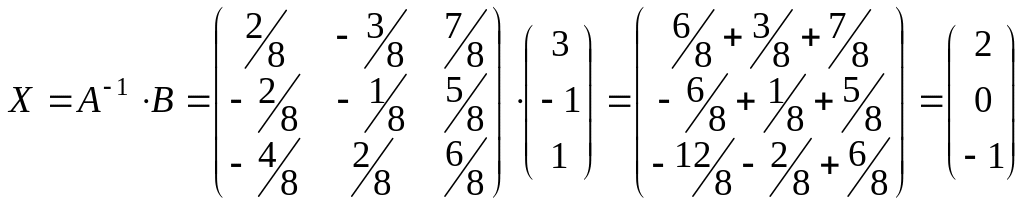 .
.
О твет:
Метод Гаусса решения систем линейных уравнений.
П роцесс решения по методу Гаусса состоит из двух этапов.
На первом этапе система (1) приводится к одной из следующих систем:

 (2)
(2)
где
![]() ,
,
![]() .
.
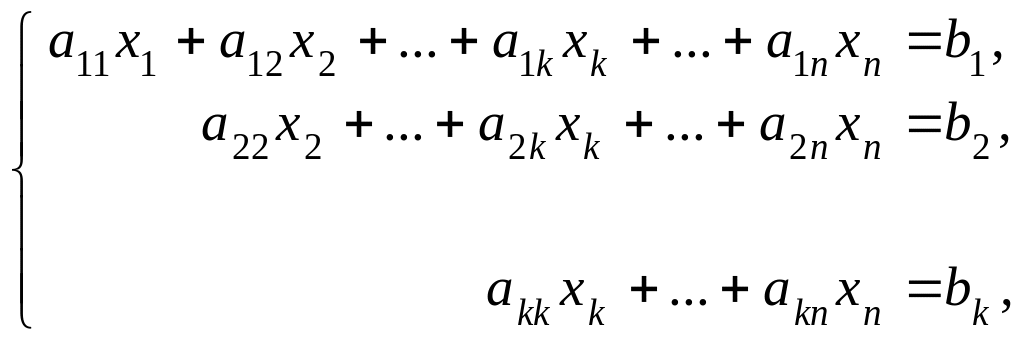
 (3)
(3)
где
![]() .
.
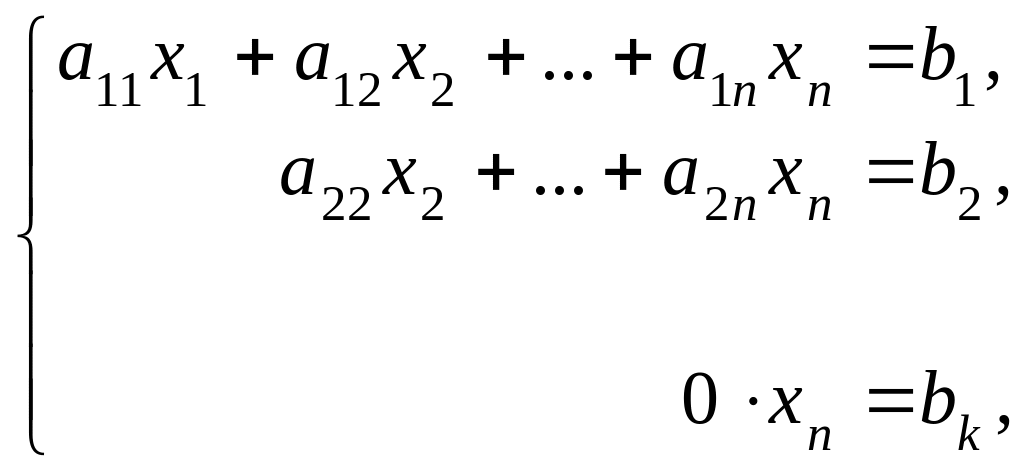
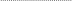 (4)
(4)
г
де
![]() .
.
На втором этапе:
система (2) имеет единственное решение, значение
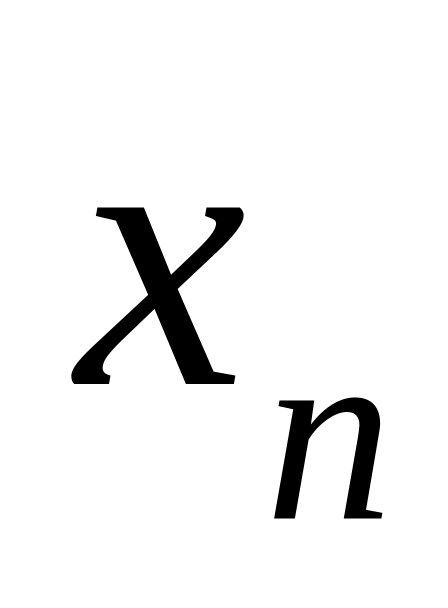 находится из последнего уравнения,
значение
находится из последнего уравнения,
значение
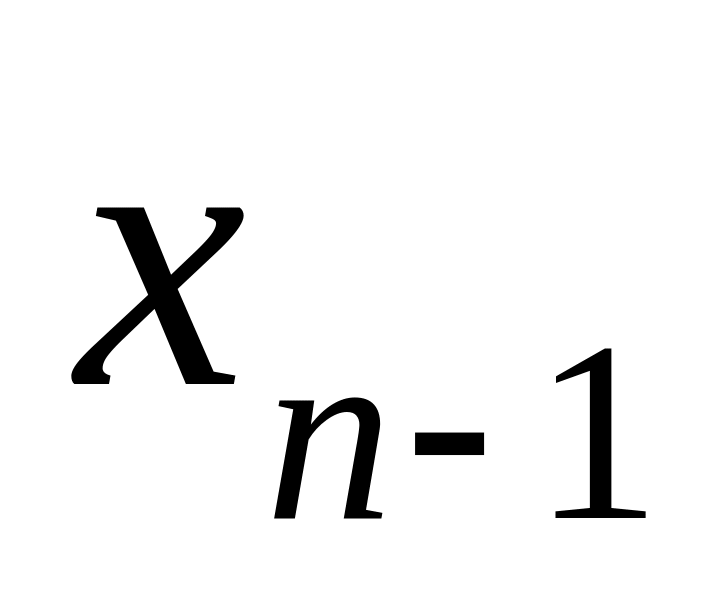 —
из предпоследнего,…,значение
—
из предпоследнего,…,значение
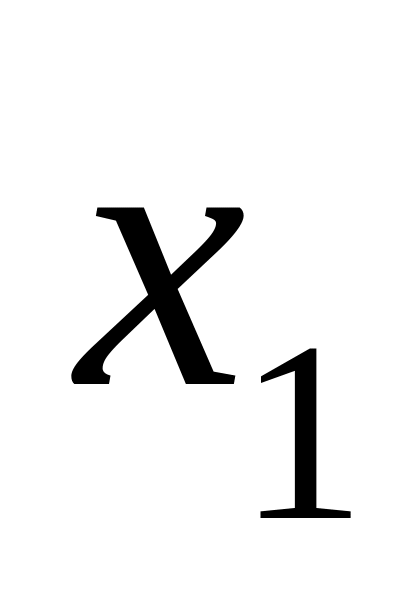 —
из первого;
—
из первого;система (3) имеет бесконечное множество решений;
система (4) несовместна, так как никакие значения неизвестных не могут удовлетворять её последнему уравнению.
-
М етод Гаусса. применим к любой (!) системе линейных уравнений.
Опишем метод Гаусса подробнее на примере.
Пример 2.4. Исследуйте систему линейных уравнений примера 2.1; и если она совместна, то найдите её решение:
I . Исследуем систему на совместность. Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
![]() ~
~![]() .
.
Очевидно,
что
![]() .
Значит, согласно
(**)
(см. §1), система совместна и определённа,
т.е. существует единственное решение.
.
Значит, согласно
(**)
(см. §1), система совместна и определённа,
т.е. существует единственное решение.
II.
Найдём решение системы.
Запишем систему уравнений, соответствующую
полученной расширенной матрице:
![]() Имеем систему вида (2). Из второго уравнения
Имеем систему вида (2). Из второго уравнения
![]() .
Подставляя это значение в первое
уравнение, получим:
.
Подставляя это значение в первое
уравнение, получим:
![]() .
.
О твет:
Пример
2.5.
Исследуйте систему линейных уравнений
примера 2.3, и если она совместна, то
найдите её решение:
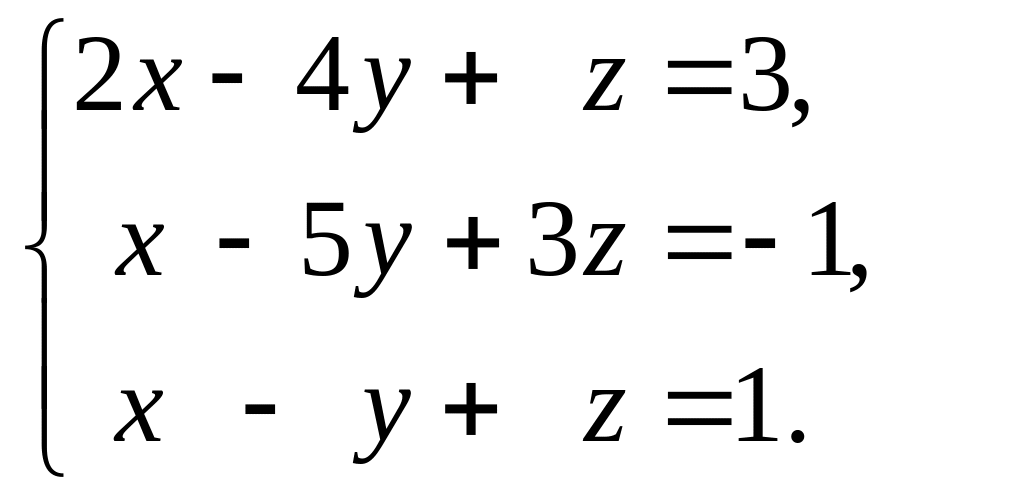
I . Исследуем систему на совместность. Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
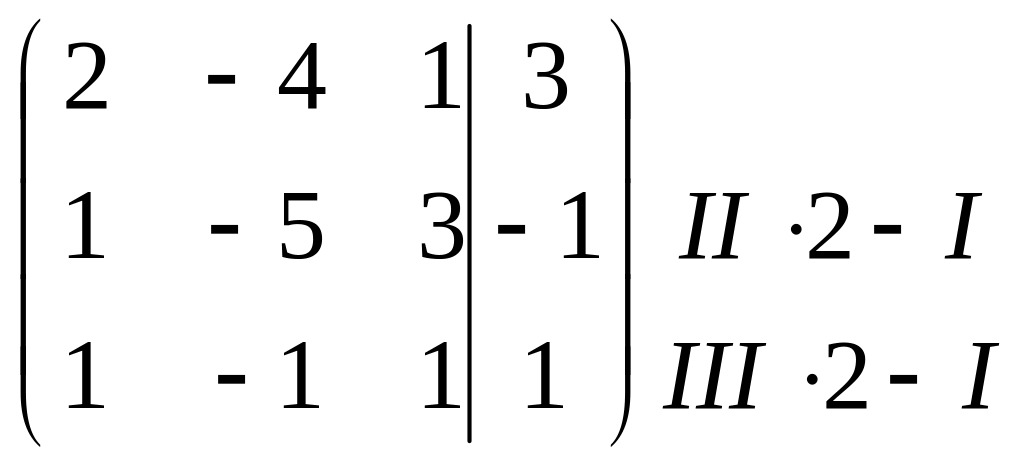 ~
~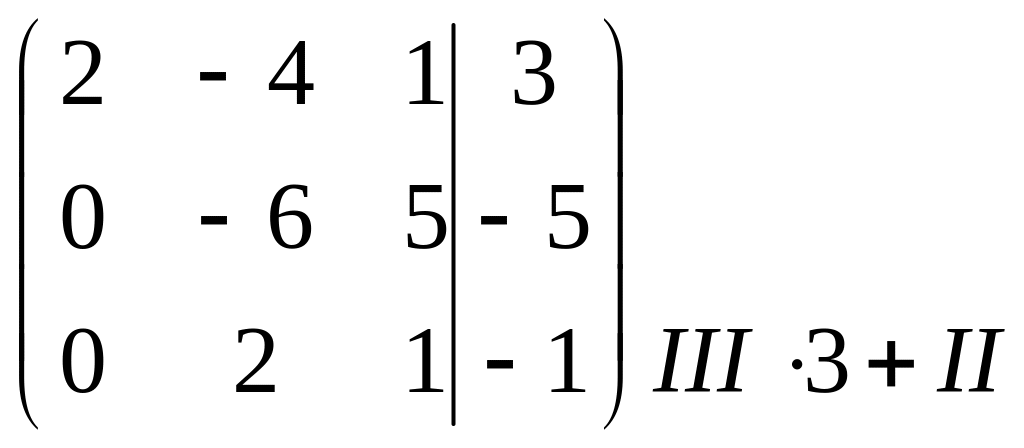 ~
~
~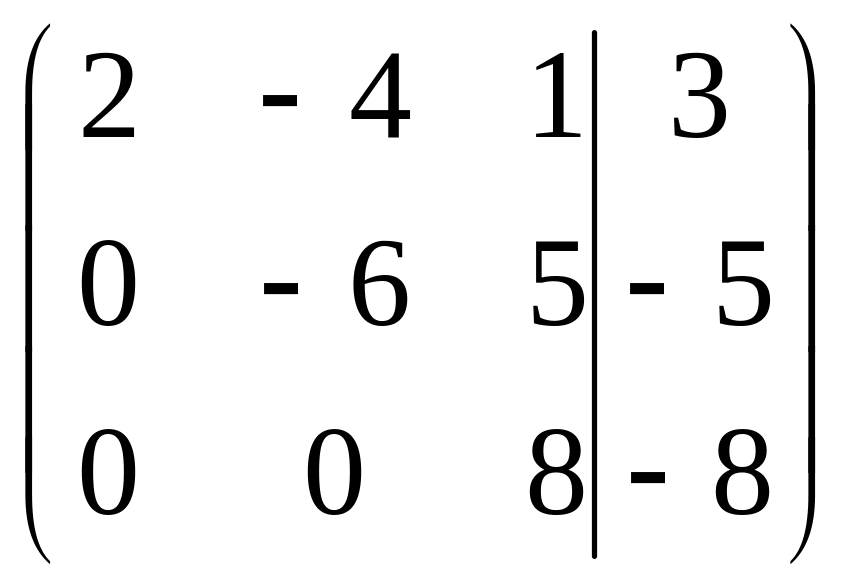 .
.
Очевидно,
что
![]() .
Значит, согласно
(**)
(см. §1), система совместна и определённа,
т.е. существует единственное решение.
.
Значит, согласно
(**)
(см. §1), система совместна и определённа,
т.е. существует единственное решение.
II.
Найдём решение системы.
Запишем систему уравнений, соответствующую
полученной расширенной матрице:
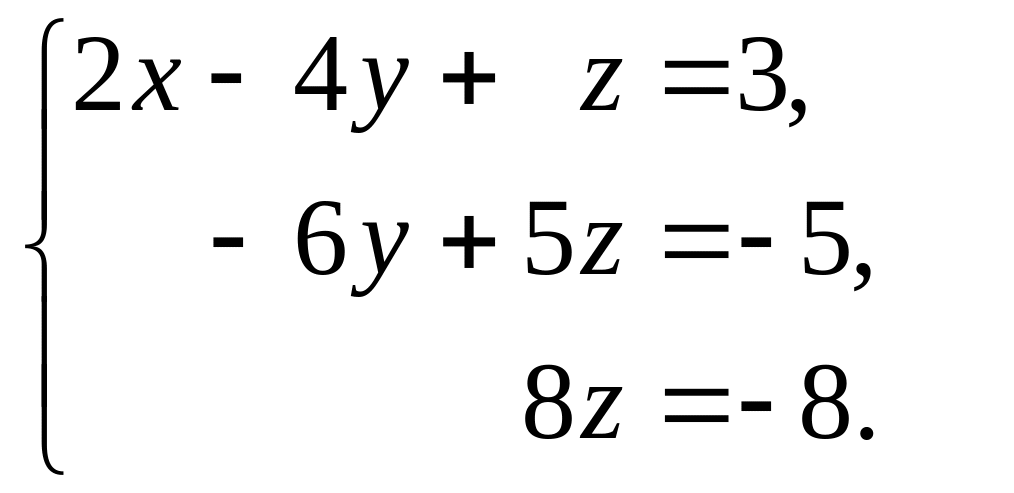
Имеем
систему вида (2). Из третьего уравнения
![]() .
.
Подставляя
это значение во второе уравнение,
получим:
![]() .
.
Подставляя
найденные значения
![]() в первое уравнение, получим:
в первое уравнение, получим:
![]() .
.
О
твет:
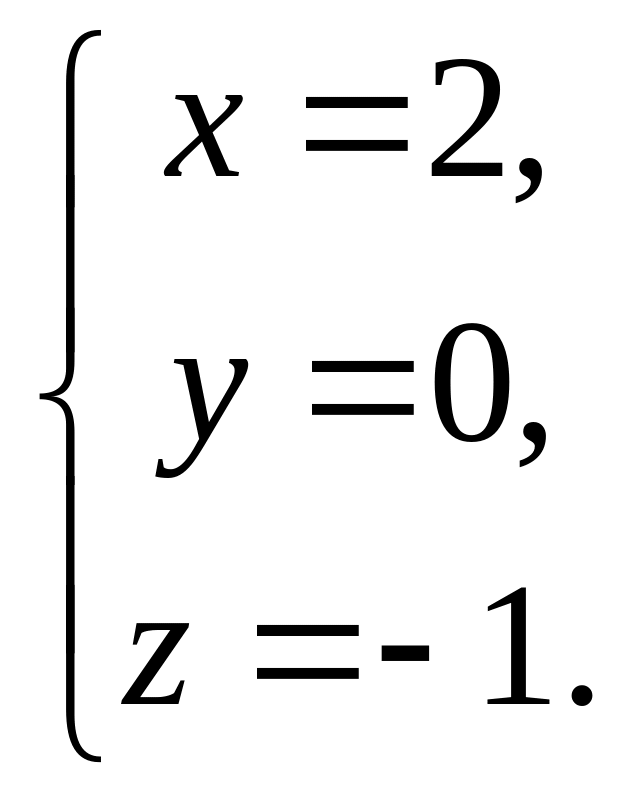
Пример
2.6.
Исследуйте систему линейных уравнений,
и если она совместна, то найдите её
решение:
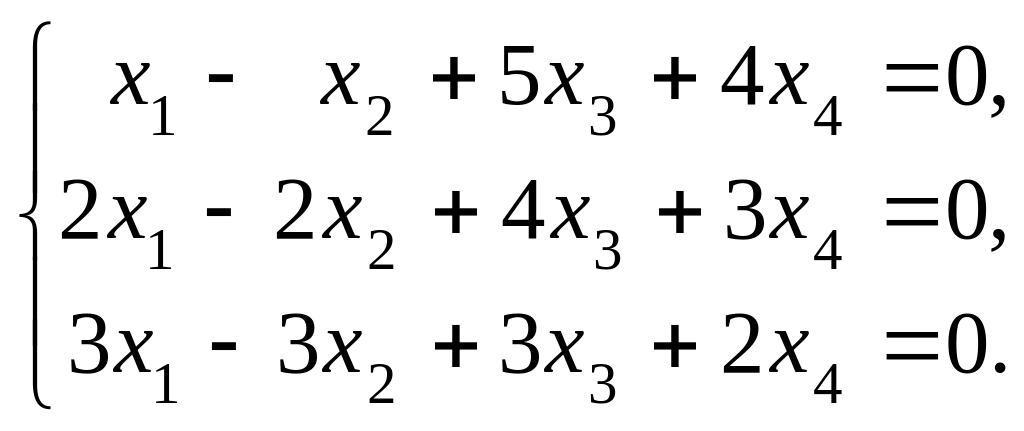
I . Исследуем систему на совместность. Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
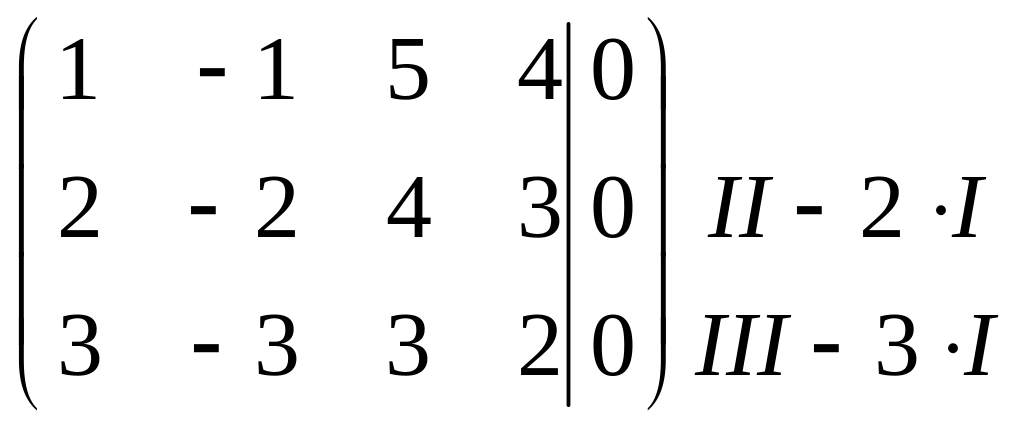 ~
~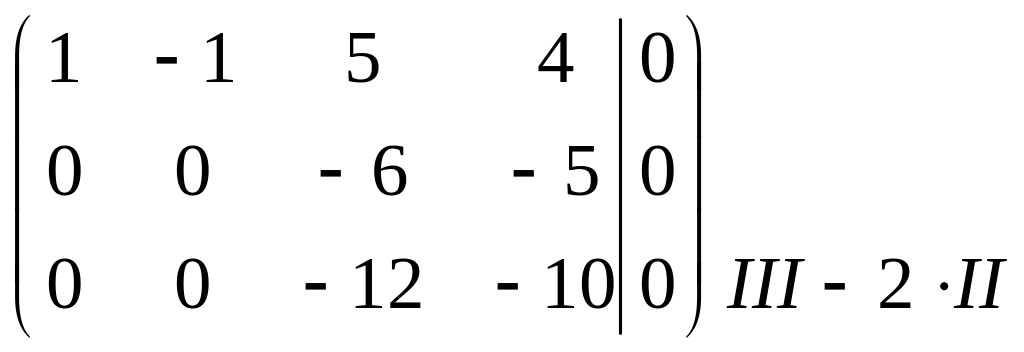 ~~
~~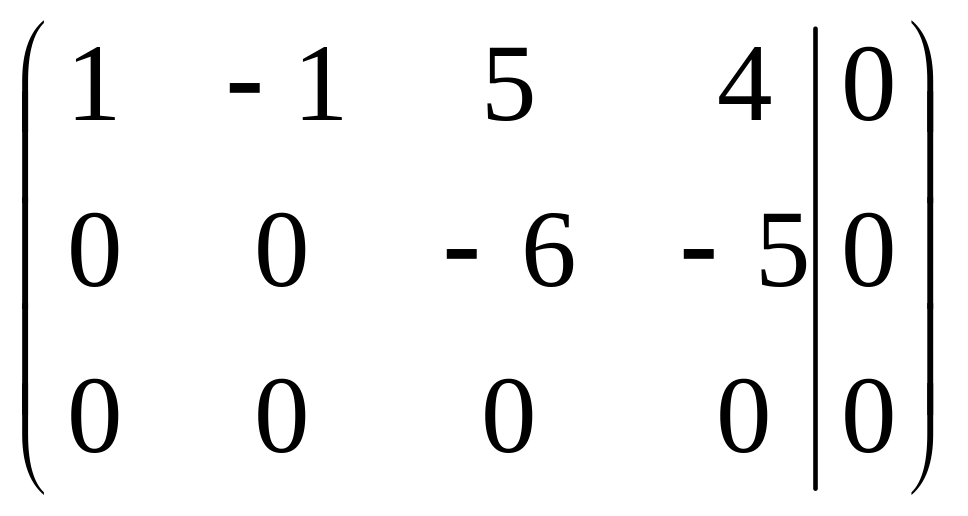 .
.
Очевидно,
что
![]() .
Значит, согласно
(***)
(см. §1), система совместна и неопределённа,
т.е. имеет бесконечно много решений.
.
Значит, согласно
(***)
(см. §1), система совместна и неопределённа,
т.е. имеет бесконечно много решений.
II. Найдём решение системы. Запишем систему уравнений, соответствующую полученной расширенной матрице:
![]()
Имеем
систему вида (3). Выразим
![]() из второго уравнения и подставим
полученное выражение в первое уравнение:
из второго уравнения и подставим
полученное выражение в первое уравнение:
![]()
![]() .
.
Следовательно,
исходная система имеет решение
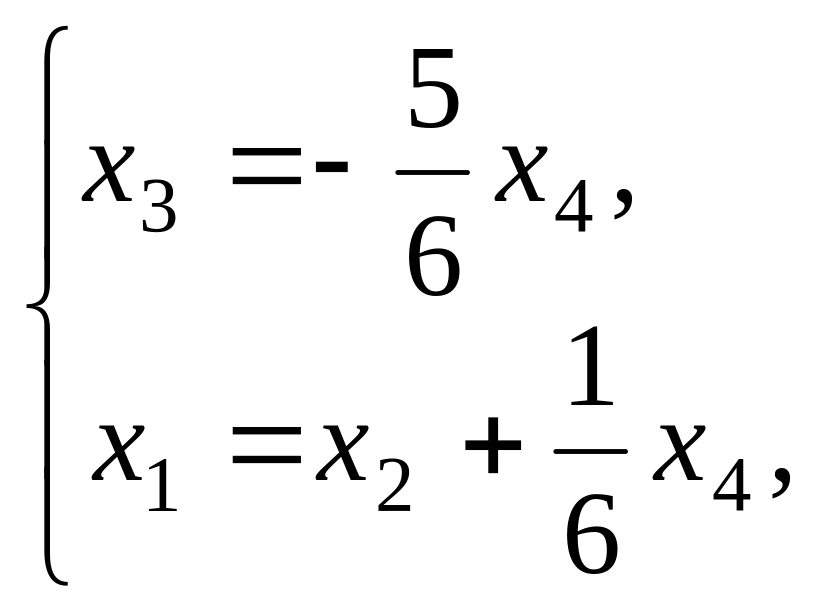 где
где
![]() ,
,
![]() могут принимать любые действительные
значения.
могут принимать любые действительные
значения.
О
твет:
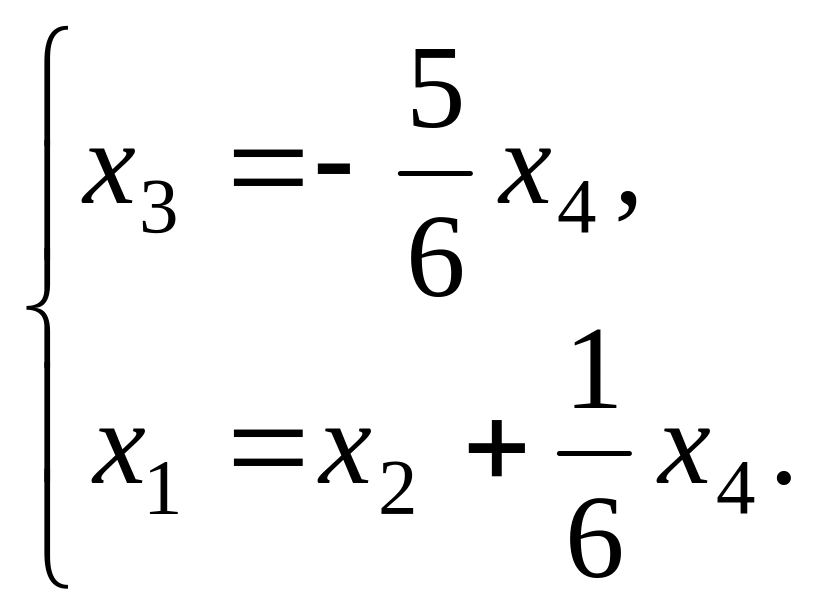
Продукт |
Сырье |
|
I |
II |
|
|
3 |
1,5 |
|
2 |
4 |
Запасы |
60 |
75 |
Может ли цех удовлетворить заказ трёх торговых организаций:
Продукт |
Заказ I организации |
Заказ II организации |
Заказ III организации |
|
2 |
3 |
3 |
|
5 |
6 |
4 |
П
усть
![]() и
и
![]() —
количество
единиц продукции
и
соответственно,
которое может выпустить цех при данных
условиях производства. Тогда
данные первой таблицы можно представить
системой уравнений:
—
количество
единиц продукции
и
соответственно,
которое может выпустить цех при данных
условиях производства. Тогда
данные первой таблицы можно представить
системой уравнений:
![]()
Решим её методом Гаусса.
![]() ~
~![]()
![]()
![]()
![]()
Т.е. цех произведёт 10 единиц продукта , 15 единиц — продукта .
Выясним, сможет ли цех выполнить заказ.
Д
ля
выполнения заказа нужно
![]() единиц продукта
и
единиц продукта
и
![]() единиц продукта
.
Следовательно, цех
может выполнить заказ.
единиц продукта
.
Следовательно, цех
может выполнить заказ.
ЧТО ДОЛЖЕН ЗНАТЬ СТУДЕНТ
1. Понятие системы линейных уравнений с неизвестными.
2. Матричный способ решения системы уравнений (метод обратной матрицы).
3. Метод Крамера решения систем уравнений.
4. Метод Гаусса решения систем уравнений.
5. Понятие однородных систем уравнений.
6. Теорема Кронекера-Капелли.
