§ 5. Признаки возрастания и убывания функций. Интервалы монотонности функций.

Е сли для всех точек отрезка при выполняется равенство , то функция называется возрастающей на .

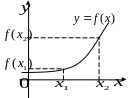
При выполнении условий , функция называется убывающей на .

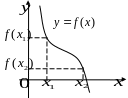
Интервалы, в которых функция только возрастает или только убывает, называются интервалами монотонности функции.

П ризнак возрастания. Дифференцируемая функция возрастает на отрезке тогда и только тогда, когда её производная .

П ризнак убывания. Дифференцируемая функция убывает на отрезке тогда и только тогда, когда её производная .

В точках, отделяющих интервалы монотонности функции, производная функции обращается в нуль или не существует. Эти точки называются критическими.

Для нахождения интервалов монотонности функции необходимо найти все её критические точки и установить знак производной в каждом из интервалов, на которые критические точки разбивают область существования функции.

Пример 7.13. Найдите интервалы монотонности функции .

Ф ункция определена на всей числовой оси. Найдём её производную. .

Найдём критические точки, приравняв производную к нулю.

— критические. Результаты исследования занесём в таблицу:

	+				+

Т аким образом, функция возрастает а интервалах и , а убывает на интервале .

§ 6. Экстремум функции. Необходимый признак.

Т очка называется точкой максимума (maximum) функции , если значение функции в этой точке больше её значений во всех точках некоторого интервала, содержащего точку , т.е. для любого ( — мало по величине).

Т очка называется точкой минимума (minimum) функции , если значение функции в этой точке меньше её значений во всех точках некоторого интервала, содержащего точку , т.е. .

Точки, в которых функция достигает максимума или минимума, называются точками экстремума функции, а значения функции в этих точках называют экстремальными.

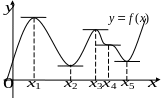
Ф ункция, заданная кривой на рисунке выше, в точках и достигает максимума, в точках и — минимума, в точке — экстремума нет. Очевидно, что функция имеет производную, равную нулю в критических точках. Касательная к кривой в этих точках параллельна оси .

Необходимый признак экстремума. Если дифференцируемая функция достигает в некоторой точке экстремума, то её производная в этой точке равна нулю или не существует.

§ 7. Достаточные признаки экстремума функции.

П ервый достаточный признак. Пусть функция непрерывна в некотором интервале, содержащем критическую точку и дифференцируема во всех точках этого интервала (кроме, быть может самой точки ). Тогда, если:

а) при , при , то в точке функция достигает максимума;

б) при , при , то в точке функция достигает минимума.

В торой достаточный признак экстремума. Пусть функция имеет в точке производную и непрерывную вторую производную . Тогда, если в точке будет максимум, а если в точке будет минимум.

Пример 7.14. В примере 7.13 точки являются точками экстремума. В точке функция достигает максимума, в точке функция достигает минимума.

Пример 7.15. Издержки предприятия выражаются формулой , где — объём производства. При каком объёме производства средние издержки будут минимальными?

С редние издержки выражаются формулой . Найдем минимум этой функции.

.

.

Найдем вторую производную функции.

, значит, по второму достаточному признаку экстремума при средние издержки достигают минимума.