Контрольный тест

1. Элемент определителя равен:

a) 0; б) 3; в) 7; г) 1.

2. Минор элемента 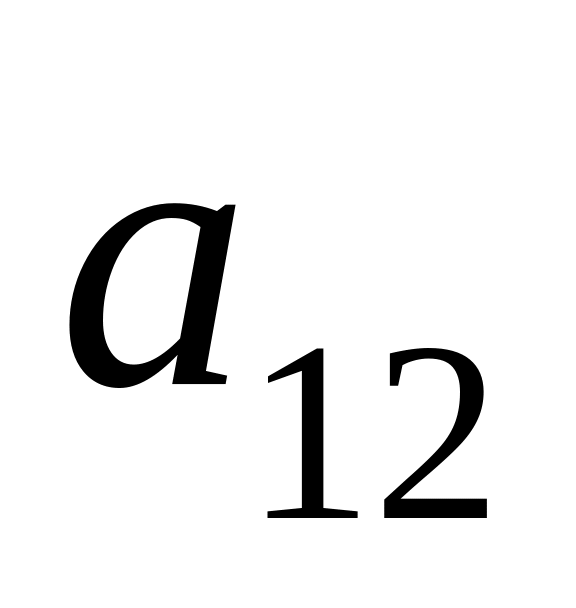определителя равен:

a) 2; б) 4; в) 3; г) 1.

3. Определитель равен:

a) 10; б) 8; в) 0; г) 1.

4. Алгебраическое дополнение элемента 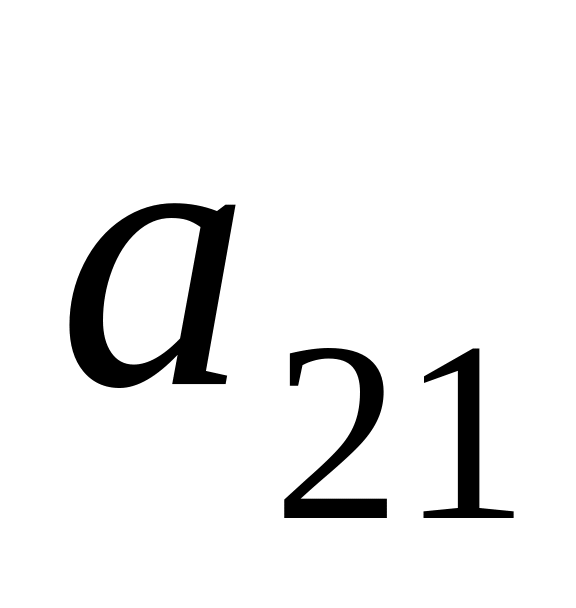определителя 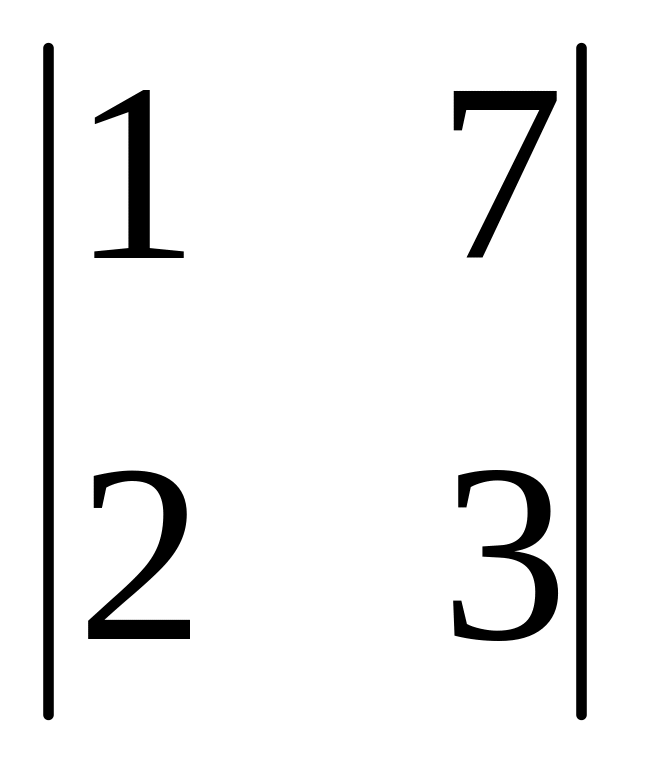равно:

a) 3; б) 7; в) 2; г) -7.

5. Определителем порядка называется:

a) таблица чисел; б) число; в) число, записанное в виде квадратной таблицы, в которой строк и столбцов; г) чисел.

6. Единичной матрицей является:

a) ; б) ; в) ; г) .

7. Сумма 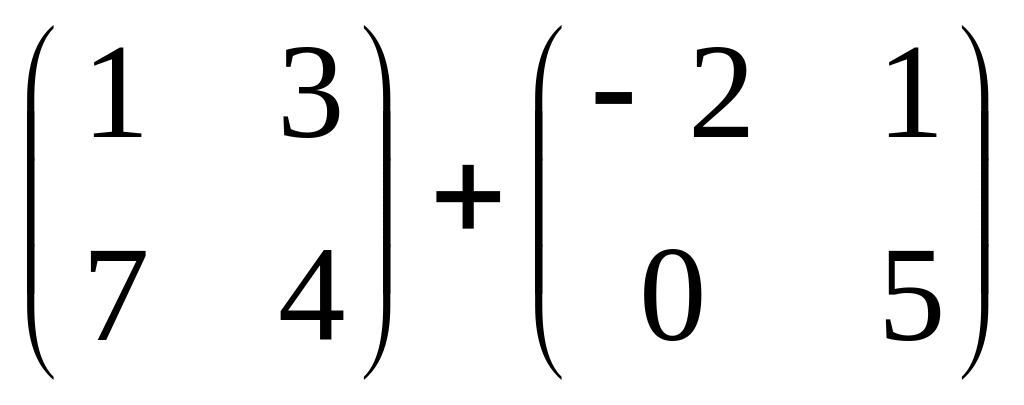равна:

a) ; б) ; в) ; г) .

8. Обратной матрицей к матрице 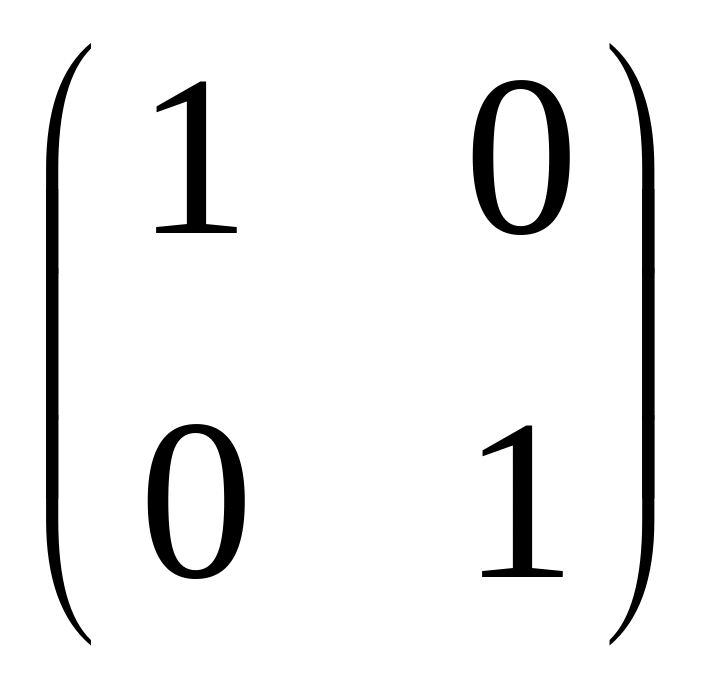является:

a) ; б) ; в) ; г) .

9. Если , то равно:

a) -1; б) 1; в) 0; г) 2.

10. Обратная матрица не обладает свойством:

a) ; б) ; в) ; г) .

Задачи для самостоятельного решения

Определители квадратных матриц

Задача 1.1. Найдите минор элемента и алгебраическое дополнение элемента определителя .

Ответ: ; .

Задача 1.2. Вычислите определитель 2-го порядка: . Ответ: 1.

Задача 1.3. Вычислите определитель третьего порядка:

а) 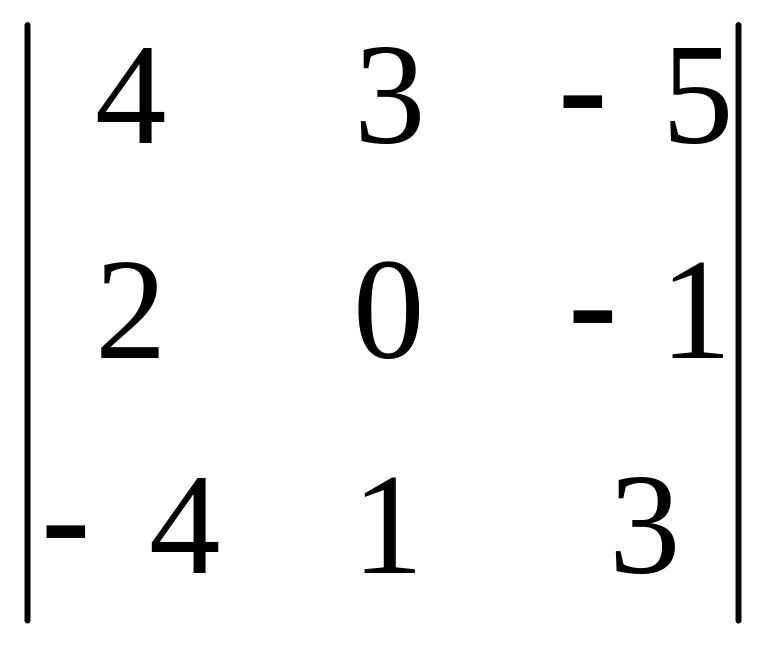; б) ; в) ; г)

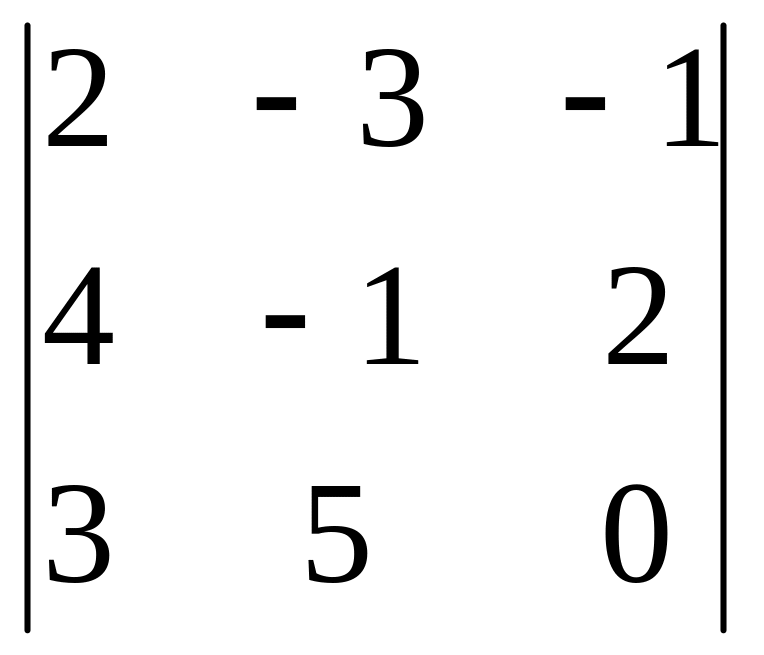
Ответ: а) -12; б) 0; в) -15; г) -61.

Задача 1.4. Найдите неизвестное число из уравнения: 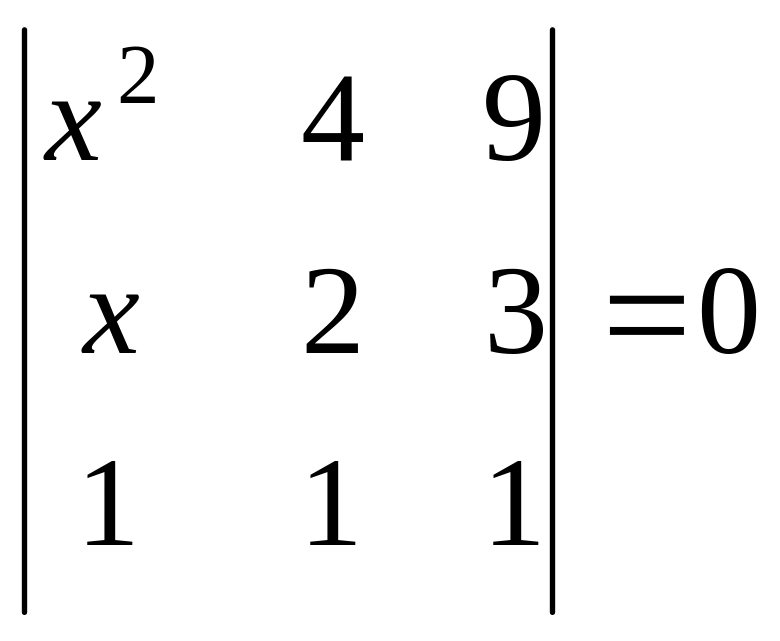. Ответ: или .

Задача 1.5. Найдите определитель четвертого порядка 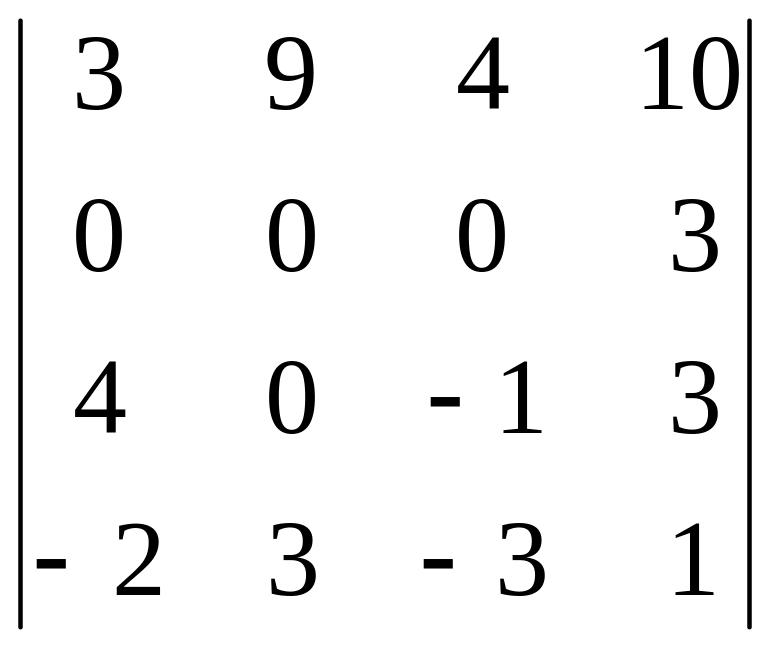. Ответ: 549.

Матрицы. Основные операции над матрицами

Задача 1.6. Найдите , если , .

Ответ: .

Задача 1.7. Найдите произведение матриц

и . Ответ: .

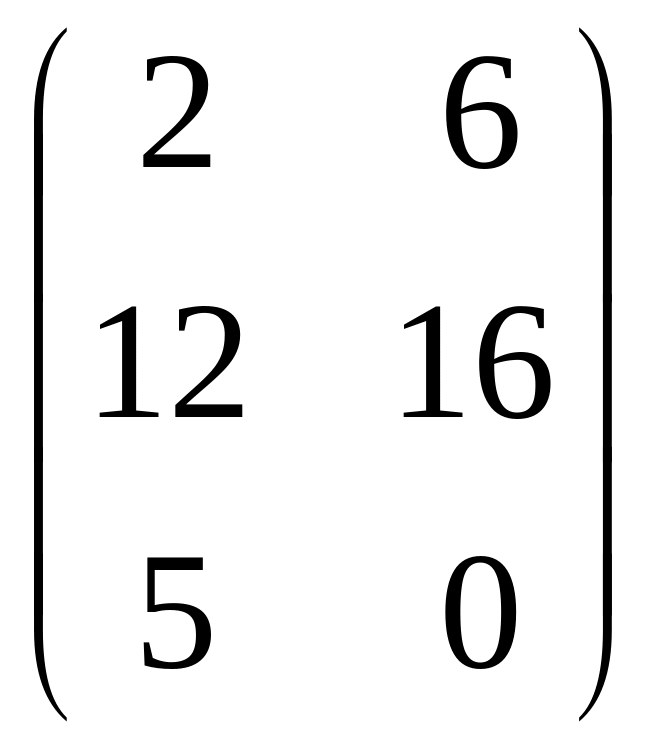Задача 1.8. Проверьте, выполняются ли равенства , для матриц:

, , .

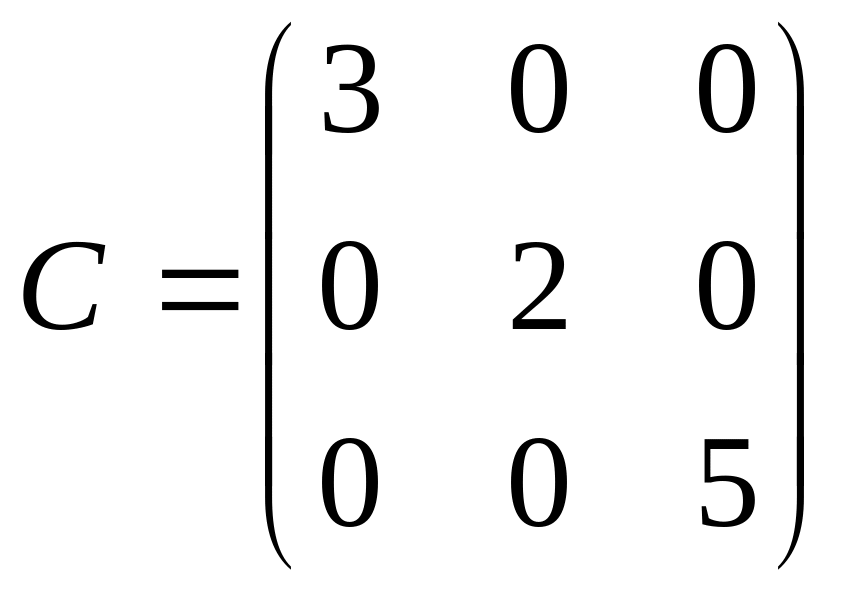Ответ: равенства верны.

Транспонирование матриц

Задача 1.9. Вычислите , если

, , . Ответ: .

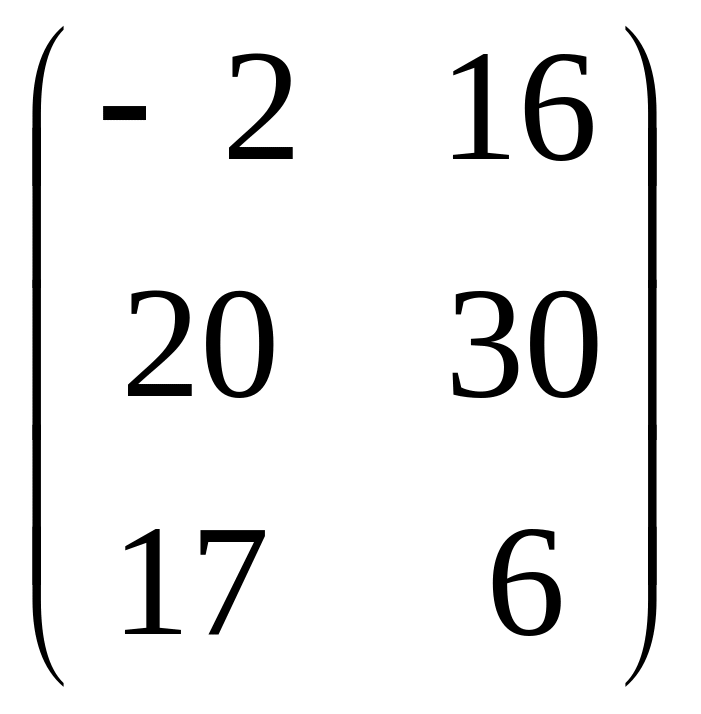Обратная матрица

Задача 1.10. Проверьте, что матрица является обратной к матрице .

Задача 1.11. Найдите для матрицы

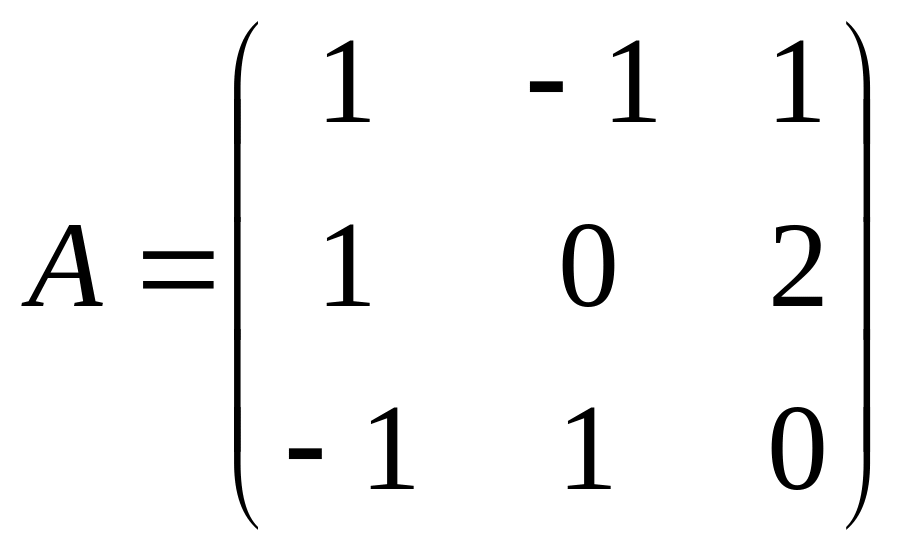. Ответ: .

Ранг матрицы. Элементарные преобразования матрицы

Задача 1.12. Приведите к ступенчатому виду матрицы 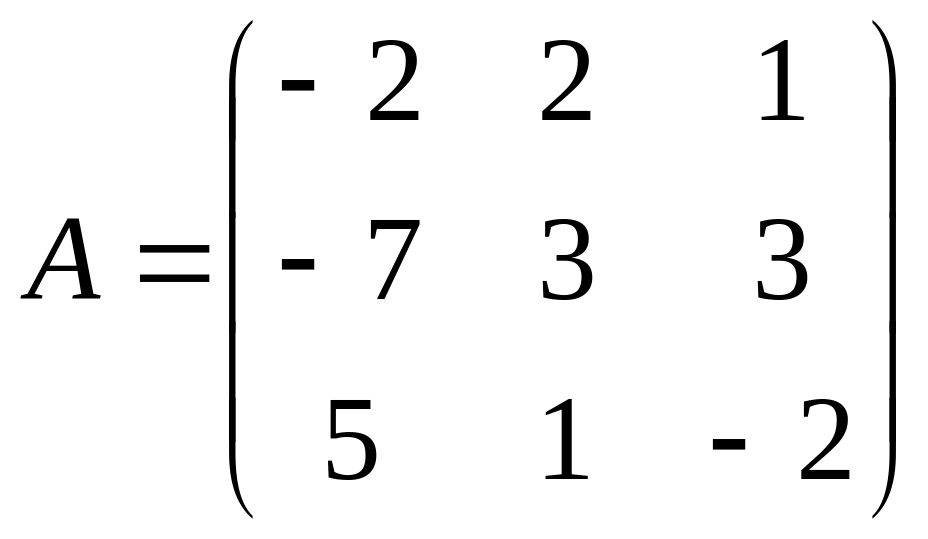, . Найдите их ранги.

Ответ: ; .

М ОДУЛЬ 2. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ

§ 1. Теорема Кронекера-Капелли

Пусть задана система из линейных уравнений с неизвестными :

(1)

г де числа называются коэффициентами системы,

а числа — свободными членами.

Решением системы (1) называется такой набор чисел , что при его подстановке в систему вместо соответствующих неизвестных ( вместо ,…, вместо ) каждое из уравнений системы обращается в тождество.

С овместной называется система, которая имеет хотя бы одно решение.

Н есовместной называется система, которая не имеет ни одно го решения.

О пределённой называется система, которая имеет единственное решение.

Н еопределённой называется система, которая имеет более одного решения.

О днородной называется система, если . В противном случае система называется неоднородной.

Матрицей системы называется матрица, составленная из коэффициентов системы:

.

Расширенной матрицей системы называется матрица

.

Т еорема Кронекера-Капелли. Cистема линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы:

И сследовать систему линейных уравнений означает определить, совместна она или нет, а для совместной системы — выяснить, определённа она или нет. При этом возможны три варианта:

1) Если , то система несовместна. (*)

2 ) Если , где — число неизвестных, то система совместна и определённа. (**)

3) Если , то система совместна и неопределённа. (***)