§ 1. Производная функции,

её геометрический, механический

и экономический смысл.

Л юбое изменение независимой переменной , равное разности , называется приращением этой переменной.

Р азность называется приращением функции на отрезке или , где .

Производной функции называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, т.е.

.

Функция, имеющая в данной точке конечную производную, называется дифференцируемой в этой точке.

Пример 7.1. Пользуясь определением, найдите производную функции .

П ридадим аргументу приращение . Тогда соответствующее приращение функции будет иметь вид

.

Отсюда находим предел отношения в точке при :

.

Т аким образом, .

Т еорема. Если функция дифференцируема в некоторой точке , то она непрерывна в этой точке.

О днако, обратное утверждение вообще говоря не верно. Существуют непрерывные, но не дифференцируемые функции. Например, при .

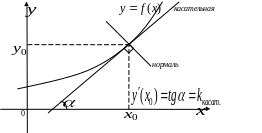
Геометрический смысл производной

Производная функции в точке равна угловому коэффициенту касательной, проведенной к кривой в точке с абсциссой .

Механический смысл производной

Скорость прямолинейного движения материальной точки в момент времени есть производная от пути по времени .

Физический смысл производной

О бобщая, можно сказать, что если функция описывает какой-либо физический процесс, то производная есть скорость протекания этого процесса.

Экономический смысл производной

Всякая хозяйственная (экономическая) деятельность человека осуществляется им для достижения некоторого результата и требует определённых усилий . Если функция описывает некоторый экономический процесс, то её производная характеризует предельную эффективность этого процесса.

Пример 7.2. Пусть — объём выпущенной продукции, а — затраты на её производство.

П редположим, что количество продукции увеличивается на . Количеству продукции соответствуют издержки производства . Следовательно, приращению количества продукции соответствует приращение издержек производства продукции . Отношение представляет собой среднее приращение издержек производства (т.е. приращение издержек производства на единицу приращения количества продукции). Тогда производная описывает предельные издержки производства при заданном объёме выпускаемой продукции.

П ример 7.3. Пусть — объём продаж, а — общая выручка от них. Тогда производная характеризует предельную выручку на заданном уровне продаж .

П ри анализе экономических явлений часто предпочитают использовать не производную функции, а особое понятие — эластичность функции.

Эластичностью функции называют предел отношения относительного приращения функции к относительному приращению аргумента при , т.е.

Эластичность относительно есть приближенный процентный прирост функции (повышение или понижение), соответствующий приращению независимой переменной на 1%. В этом заключается экономический смысл эластичности функции.